Dạng bài tìm m để phương trình có 2 nghiệm x1 x2 thỏa mãn điều kiện đã cho là một trong những dạng bài khá phổ biến hiện nay dành cho học sinh cấp 2, cấp 3. Vậy ngay sau đây, chúng tôi sẽ đưa ra một số thông tin liên quan đến dạng bài này.
Mục lục bài viết
- 1 1. Kiến thức cần nhớ khi làm dạng bài tìm m để phương trình có 2 nghiệm x1, x2 thỏa mãn điều kiện cho trước:
- 2 2. Tìm m để phương trình có 2 nghiệm x1 x2 thỏa mãn điều kiện đã cho:
- 3 3. Bài tập trắc nghiệm có lời giải:
- 4 4. Bài tập tự luyện về bài toán tìm m để phương trình có 2 nghiệm x1, x2 thỏa mãn điều kiện cho trước:
1. Kiến thức cần nhớ khi làm dạng bài tìm m để phương trình có 2 nghiệm x1, x2 thỏa mãn điều kiện cho trước:
Cách giải dạng bài tìm m thỏa mãn điều kiện cho trước
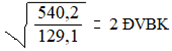
+ Đối chiếu với điều kiện xác định của tham số để xác định giá trị cần tìm
2. Tìm m để phương trình có 2 nghiệm x1 x2 thỏa mãn điều kiện đã cho:
Bài 1: Cho phương trình bậc hai (x là ẩn số, m là tham số)
a, Chứng minh phương trình trên luôn có 2 nghiệm phân biệt x1, x2 với mọi m khác 2
b, Tìm m để hai nghiệm x1, x2 của phương trình thỏa mãn hệ thức:
Hướng dẫn:
a) Để chứng minh phương trình bậc hai luôn có hai nghiệm, ta chứng minh ∆ luôn dương với mọi giá trị của tham số.
b) Khi phương trình đã có 2 nghiệm phân biệt, ta áp dụng Vi-ét để thay vào hệ thức và tìm giá trị của tham số.
Lời giải:

Bài 2: Cho phương trình (x là ẩn số, m là tham số)
a, Chứng minh phương trình luôn luôn có hai nghiệm phân biệt với mọi m
b, Tìm m để hai nghiệm phân biệt x1, x2 của phương trình thỏa mãn
Hướng dẫn:
a) Để chứng minh phương trình bậc hai luôn có hai nghiệm, ta chứng minh ∆ luôn dương với mọi giá trị của tham số.
b) Khi phương trình đã có 2 nghiệm phân biệt, ta áp dụng Vi-ét để thay vào hệ thức và tìm giá trị của tham số.
Lời giải:

Bài 3: Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn
Hướng dẫn:
Bước 1: Tìm điều kiện của tham số để phương trình có hai nghiệm phân biệt.
Bước 2: Khi phương trình đã có hai nghiệm phân biệt, ta áp dụng Vi-ét để tìm các giá trị của tham số.
Bước 3. Đối chiếu với điều kiện và kết luận bài toán.
Lời giải:
Để phương trình có hai nghiệm phân biệt


Hướng dẫn:
Bước 1: Tìm điều kiện của tham số để phương trình có hai nghiệm phân biệt.
Bước 2: Khi phương trình đã có hai nghiệm phân biệt, ta áp dụng Vi-ét để tìm các giá trị của tham số.
Bước 3. Đối chiếu với điều kiện và kết luận bài toán.
Lời giải:

3. Bài tập trắc nghiệm có lời giải:
Câu 1: Cho phương trình x2 – (2m + 2)x + 2m = 0 (m là tham số). Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn ![]()
A. m = 0
B. m = 1
C. m = 3
D. m = 4
Giải
Phương trình x2 – (2m + 2)x + 2m = 0 ⇔ x2 – 2(m + 1)x + 2m = 0
Điều kiện PT có 2 nghiệm không âm x1, x2 là
Vậy m = 0 là giá trị cần tìm.
Đáp án đúng là A
Câu 2: Cho phương trình x2 + 2x – m2 – 1 = 0 (m là tham số)
Tìm m để phương trình trên có hai nghiệm thỏa mãn x1 = -3x2
A. m = 3
B. m = ±1
C. m = ±√2
D. m = -2
Giải
Ta có: Δ’ = 12 – 1.(-m2 – 1)=1 + m2 + 1 = m2 + 2 > 0 (luôn đúng với mọi m)
Suy ra phương trình luôn có hai nghiệm phân biệt với mọi m.
Theo Vi-ét ta có: 
Ta có: x1 + x2 = -2 (do trên) và x1 = -3x2 nên có hệ phương trình sau:

Vậy m = ±√2 là các giá trị cần tìm.
Đáp án đúng là C
Câu 3: Cho phương trình x2 – 2(m + 1)x + m2 + m – 1 = 0 (m là tham số)
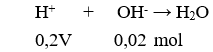
Do đó:
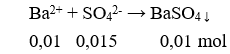
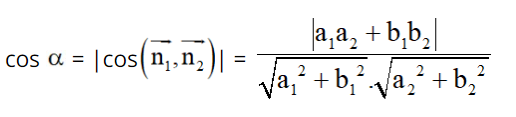
Giải
Để phương trình đã cho có hai nghiệm phân biệt thì ∆ ≥ 0
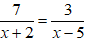
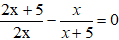
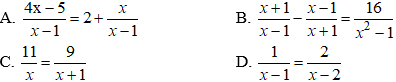
Tìm m để phương trình có hai nghiệm là số đo của 2 cạnh góc vuông của tam giác vuông có cạnh huyền bằng 3.
A. m = ±2
B. m = ±√2
C. m = – 1
D. m = 0
Giải

Theo đề bài x1, x2 là số đo của 2 cạnh góc vuông của tam giác vuông có cạnh huyền bằng 3 nên ta có:
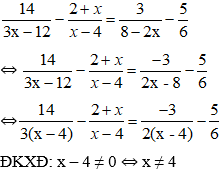
Vậy m = ±2 là các giá trị cần tìm.
Đáp án đúng là A
Câu 6: Cho phương trình x2 – 2x – 2m2 = 0 với x là ẩn số.
Tìm giá trị của m để hai nghiệm của phương trình thỏa hệ thức x12 = 4x22.
A. m = ±2
B. m = ±1
C. m = -6
D. m = 3
Giải
Ta có: Δ’ = (-1)2 – (-2m2 )= 1 + 2m2 > 0
Suy ra phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
Giả sử phương trình có hai nghiệm x1, x2 theo hệ thức Vi-ét:
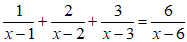
Vậy m = ±2 là giá trị cần tìm.
Đáp án đúng là A
Câu 7: Cho phương trình x2 – 5x + m = 0 (m là tham số).
Tìm m để phương trình trên có hai nghiệm x1, x2 thỏa mãn |x1 – x2| = 3.
A. m = 2
B. m = 4
C. m = 6
D. m = 8
Giải
Ta có: ∆ = 25 – 4m
Để phương trình đã cho có 2 nghiệm phân biệt x1, x2 thì ![]()
Theo Vi-ét, ta có: x1 + x2 = 5 (1) và x1.x2 = m (3)
Mặt khác theo giả thiết ta có: |x1 – x2| = 3 (2)
Giải hệ (1) và (2):
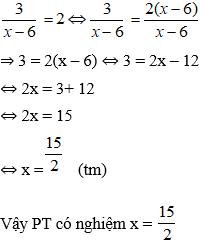
Với x1 = 4, x2 = 1 thay vào (3) ta được m = 4
Với x1 = 1, x2 = 4 thay vào (3) ta được m = 4
m = 4 thỏa mãn điều kiện (*) , vậy m = 4 là giá trị cần tìm
Đáp án đúng là B
Câu 8: Cho phương trình bậc hai x2 + 2(m – 1)x – (m + 1)= 0
Tìm giá trị m để phương trình có một nghiệm lớn hơn và một nghiệm nhỏ hơn 1.
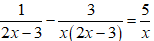
Suy ra phương trình luôn có hai nghiệm phân biệt x1, x2 với mọi m.

Đáp án đúng là C
Câu 9: Cho phương trình bậc hai: x2 + 2(m – 1)x – (m + 1) = 0
Tìm giá trị m để phương trình có hai nghiệm lớn hơn 2
A. m > – 1
B. m > 2
C. m < 2
D. m < 0
Giải
Để phương trình có hai nghiệm đều nhỏ hơn 2 thì:
Vậy đáp án đúng là D
Câu 10: Cho phương trình x2 – (2m + 3)x + m2 + 3m + 2 = 0
Xác định m để phương trình có hai nghiệm thỏa mãn -3 < x1 < x2 < 6
A. m > 1
B. -2 < m < 2
C. -4 < m < 4
D. m < 3
Giải
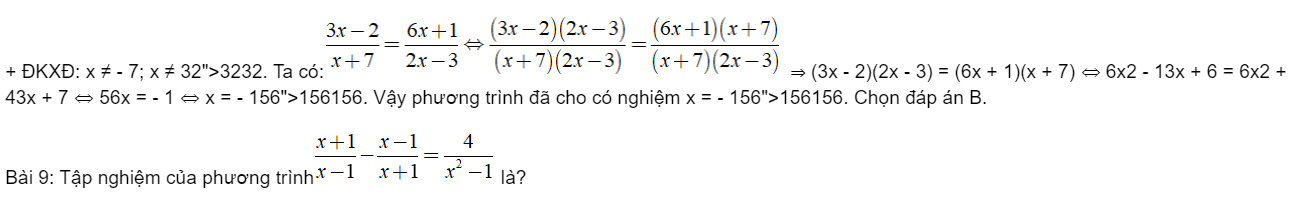
Vì -3 < x1 < x2 < 6 nên

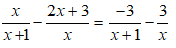
Vậy -4 < m < 4.
Đáp án đúng là C
4. Bài tập tự luyện về bài toán tìm m để phương trình có 2 nghiệm x1, x2 thỏa mãn điều kiện cho trước:
Bài 1: Cho phương trình: x2 – 14x + 29 = 0 có hai nghiệm x1, x2
Hãy tính:
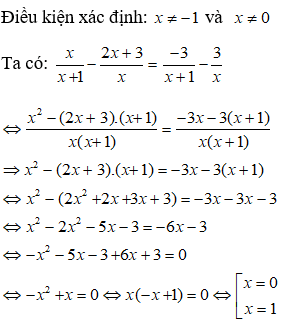
Bài 2: Cho phương trình x2 – 2(m + 1)x + m – 4 = 0, m là tham số.
a) Giải phương trình khi m = -5.
b) Chứng minh rằng: Phương trình luôn có nghiệm x1, x2 với mọi tham số m.
c) Tìm m để phương trình có hai nghiệm trái dấu.
d) Tìm m để phương trình có hai nghiệm dương.
e) Chứng minh rằng biểu thức A = x1(1 – x2) + x2(x – x1) không phụ thuộc tham số m.
Bài 3: Cho phương trình ẩn x: (m – a)x2 + 2mx + m – 2 = 0
a) Giải phương trình khi m = 5.
b) Tìm m để phương trình có nghiệm . Tìm nghiệm còn lại.
c) Tìm m để phương trình có nghiệm? Có 2 nghiệm phân biệt? Vô nghiệm? Có nghiệm kép?
d) Khi phương trình có nghiệm x1, x2 hãy tính:
i) A = x21 + x22 theo tham số m.
ii) Tìm m để A = 1
Bài 4: Cho phương trình (m tham số)
a, Chứng minh phương trình trên luôn có nghiệm với mọi giá trị của m
b, Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn
Bài 5: Cho phương trình
a, Giải phương trình khi m = – 2
b, Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn x1 =2×2
Bài 6: Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn
Bài 7: Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn
Bài 8: Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn
Bài 9: Tìm m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn 2×1 + 3×2 = -1




