Các trường hợp bằng nhau của tam giác vuông lớp 7

1. Tam giác vuông là tam giác gì?

Tam giác vuông là một loại tam giác đặc biệt, có một góc vuông, tức là một góc có độ lớn bằng 90 độ. Điều đặc biệt của tam giác vuông là cạnh đối diện với góc vuông được gọi là cạnh huyền, trong khi hai cạnh còn lại được gọi là cạnh góc nhọn. Đây là một trong những loại tam giác quan trọng và phổ biến nhất trong hình học.

Tính chất đáng chú ý của tam giác vuông là tính chất Pythagoras. Theo đó, độ dài của cạnh huyền bằng căn bậc hai của tổng bình phương độ dài hai cạnh góc nhọn. Đây là một công thức rất hữu ích và được sử dụng rộng rãi trong giải các bài toán liên quan đến tam giác vuông. Ví dụ, khi chúng ta biết độ dài hai cạnh góc nhọn của một tam giác vuông, chúng ta có thể tính được độ dài cạnh huyền mà không cần biết góc vuông.

Tam giác vuông cũng có một số tính chất khác. Tổng của ba góc của tam giác vuông luôn bằng 180 độ, điều này cũng áp dụng cho tất cả các loại tam giác. Diện tích của tam giác vuông bằng một nửa tích hai cạnh góc nhọn. Điều này có thể được tính toán bằng công thức diện tích tam giác: diện tích bằng một nửa tích hai cạnh góc nhọn nhân với sin góc vuông.

Ứng dụng của tam giác vuông rất phong phú trong thực tế. Ví dụ, trong lĩnh vực kiến trúc, tam giác vuông được sử dụng để tính toán chiều cao của một tòa nhà dựa trên góc nhìn từ một vị trí xa. Trong hình học, tam giác vuông được sử dụng để xác định các tỉ lệ giữa các đường thẳng và diện tích của các hình khác nhau. Ngoài ra, tam giác vuông còn được sử dụng trong các bài toán về tọa độ trong không gian, trong đo lường khoảng cách và trong các bài toán liên quan đến định vị và định hướng.

Vì các tính chất đặc biệt và ứng dụng rộng rãi của nó, tam giác vuông là một khái niệm quan trọng và cần được hiểu rõ trong lĩnh vực hình học và các bài toán liên quan.

2. Các trường hợp bằng nhau của tam giác vuông lớp 7: 

Các trường hợp bằng nhau của tam giác vuông:

– Hai cạnh góc vuông Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh). Điều này có nghĩa là nếu cạnh góc vuông AB của tam giác vuông ABC bằng cạnh góc vuông DE của tam giác vuông DEF và cạnh góc vuông BC của tam giác vuông ABC bằng cạnh góc vuông EF của tam giác vuông DEF, thì ta có thể kết luận rằng tam giác vuông ABC và tam giác vuông DEF là bằng nhau. Điều này có ứng dụng trong việc chứng minh các bài toán liên quan đến tính chất đồng dạng của tam giác vuông.

– Cạnh góc vuông và góc nhọn kề cạnh đó Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (góc – cạnh – góc). Ví dụ, nếu cạnh góc vuông AB và góc nhọn BAC của tam giác vuông ABC bằng cạnh góc vuông DE và góc nhọn DEF của tam giác vuông DEF, ta có thể kết luận rằng tam giác vuông ABC và tam giác vuông DEF là bằng nhau. Đây cũng là một trong những phương pháp chứng minh đồng dạng của tam giác vuông.

– Cạnh huyền – góc nhọn Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (góc – cạnh – góc). Ví dụ, nếu cạnh huyền AC và góc nhọn BAC của tam giác vuông ABC bằng cạnh huyền DF và góc nhọn DEF của tam giác vuông DEF, ta có thể kết luận rằng tam giác vuông ABC và tam giác vuông DEF là bằng nhau. Đây là một trong những phương pháp chứng minh đồng dạng tam giác vuông sử dụng tính chất của cạnh huyền.

– Cạnh huyền – cạnh góc vuông Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Ví dụ, nếu cạnh huyền AC và cạnh góc vuông BC của tam giác vuông ABC bằng cạnh huyền DF và cạnh góc vuông EF của tam giác vuông DEF, ta có thể kết luận rằng tam giác vuông ABC và tam giác vuông DEF là bằng nhau. Đây là một trong những phương pháp chứng minh đồng dạng tam giác vuông khi biết cạnh huyền và một cạnh góc vuông.

Tuy nhiên, cần lưu ý rằng các trường hợp này chỉ áp dụng cho tam giác vuông và không áp dụng cho các loại tam giác khác. Vì vậy, khi kiểm tra tính bằng nhau của các tam giác, chúng ta cần xác định trước rằng chúng là tam giác vuông. Đồng thời, việc áp dụng các quy tắc này trong giải các bài toán tam giác sẽ giúp chúng ta hiểu rõ hơn về tính chất đồng dạng của tam giác vuông và ứng dụng chúng vào thực tế.

3. Câu hỏi trắc nghiệm vận dụng liên quan: 

Câu 1: Cho tam giác DEF và tam giác JIK có: . Cần thêm một điều kiện gì để ΔDEF = ΔJIK theo trường hợp cạnh huyền – góc vuông?

Đáp án cần chọn là: C

Câu 2: Cho tam giác ABC và tam giác MNP có . Cần thêm một điều kiện gì để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông – góc nhọn kề?

Đáp án cần chọn là: A

Câu 3: Cho tam giác ABC và tam giác DEF có:

Tính độ dài AB biết DE = 5cm

A. 4 cm

B. 3 cm

C. 5 cm

D. 6 cm

Đáp án cần chọn là: C

Câu 4: Cho tam giác ABC và KHI có: . Phát biểu nào trong các phát biểu sau là đúng:

Đáp án cần chọn là: A

Câu 5: Cho tam giác MNP và KHI có: . Chọn khẳng định đúng.

Đáp án cần chọn là: A

Câu 6: Cho tam giác ABC và tam giác DEF có . Biết AC = 9cm. Độ dài DF là:

A. 10 cm

B. 5 cm

C. 9 cm

D. 7 cm

Đáp án cần chọn là: C

Câu 7: Cho tam giác ABC và tam giác DEF có . Biết AB = 9cm, AB = 12cm. Độ dài EF là:

A. 12 cm

B. 9 cm

C. 15 cm

D. 13 cm

Đáp án cần chọn là: C

Câu 8: Cho tam giác DEF và tam giác HKI có . Số đo góc I là:

Đáp án cần chọn là: C

Câu 9: Cho tam giác DEF và tam giác HKI có . Số đo góc K là:

Đáp án cần chọn là: B

Câu 10: Cho hình vẽ. Chọn câu đúng

Đáp án cần chọn là: D

Câu 11: Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Khi đó, tam giác ABC là tam giác gì?

Đáp án cần chọn là: D

Câu 12: Cho tam giác ABC cân tại A có: AH ⊥ BC  tại H. Tính số đo góc BAH biết  góc BAC= 50o

Đáp án cần chọn là: B

Câu 13: Cho tam giác ABC vuông cân tại A. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông goc với đường thẳng d. Khi đó BH2 + CK2 bằng:

Đáp án cần chọn là: C

Câu 14: Cho tam giác ABC vuông cân tại A, có AC = 8cm. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông góc với đường thẳng d. Khi đó BH2 + CK2 bằng:

A. 46

B. 16

C. 64

D. 48

Đáp án cần chọn là: C

Câu 15: Cho tam giác ABC vuông tại A (AB > AC). Tia phân giác của góc B cắt AC ở D. Kẻ DH vuông góc với BC. Trên tia AC lấy E sao cho AE = AB. Đường thẳng vuông góc AE tại E cắt tia BH tại K

15.1: Chọn câu đúng

Đáp án cần chọn là: D

15.2: Tính số đo góc DBK

Đáp án cần chọn là: A

Câu 16: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho MN = BC. Kẻ T

16.1: Tam giác AMN là tam giác gì?

A. Vuông cân

B. Cân

C. Đều

D. Vuông

Đáp án cần chọn là: B

16.2: So sánh BE và CF

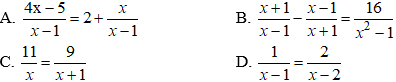
Đáp án cần chọn là: C

16.3: Chọn câu đúng

Đáp án cần chọn là: A

Câu 17: Cho tam giác ABC vuông cân tại A và D là trung điểm AC. Từ A kẻ đường vuông góc với BD, cắt BC tại E. Chọn đáp án đúng

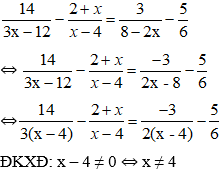
Đáp án cần chọn là: C

Câu 18: Cho tam giác ABC và tam giác NPM có . Cần thêm một điều kiện gì để tam giác ABC và tam giác NPM bằng nhau theo trường hợp cạnh huyền – góc vuông?

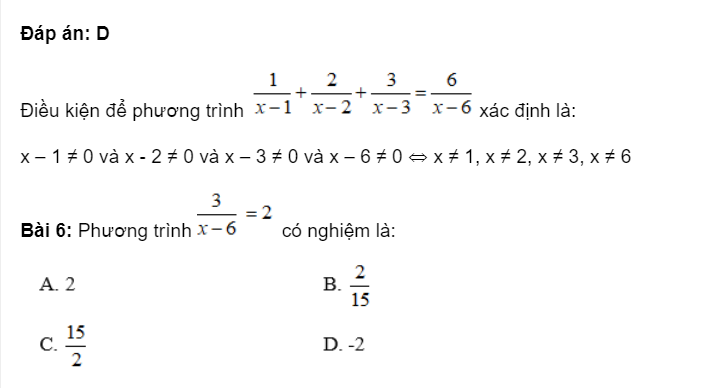
Đáp án cần chọn là: C