Vị trí tương đối của đường thẳng và đường tròn là những kiến thức cơ bản của Toán học lớp 9. Bài viết tham khảo dưới đây sẽ đưa ra những định nghĩa cơ bản về Vị trí tương đối của đường thẳng và đường tròn cũng như các bài tập vận dụng.
Mục lục bài viết
- 1 1. Định nghĩa đường tròn, đường thẳng:
- 2 2. Vị trí tương đối của đường thẳng và đường tròn:
- 3 3. Đường thẳng là cát tuyến đối với đường tròn:
- 4 4. Đường cắt trùng với đường kính và đi qua tâm của đường tròn:
- 5 5. Đường thẳng là tiếp tuyến của đường tròn:
- 6 6. Đường thẳng và đường tròn không có điểm chung:
- 7 7. Câu hỏi bài tập:
1. Định nghĩa đường tròn, đường thẳng:
Đường tròn là hình gồm tất cả các điểm trên mặt phẳng cách đều một điểm cho trước.
Đường tròn là hình gồm tất cả các điểm trong mặt phẳng cách một điểm cho trước một khoảng bằng nhau;
Đường tròn là một đường cong phẳng khép kín gồm tất cả các điểm trên mặt phẳng cách đều một điểm cho trước.
Các bộ phận của một vòng tròn
Bán kính của một vòng tròn:
Bán kính là một đoạn thẳng với một điểm cuối ở tâm của vòng tròn và điểm cuối khác trên vòng tròn.
Đường kính của một vòng tròn:
Đoạn thẳng đi qua tâm của một đường tròn và có các điểm cuối thuộc đường tròn gọi là đường kính của đường tròn.
Đường kính = 2 × bán kính
Chu vi của một vòng tròn là khoảng cách xung quanh một vòng tròn. Nó cũng giống như chu vi của các hình dạng khác.
Đường thẳng là hình một chiều vô tận không có chiều rộng. Nó là sự kết hợp của các điểm vô tận được nối ở cả hai phía của một điểm. Một đường thẳng không có bất kỳ đường cong nào trong đó. Nó có thể nằm ngang, dọc hoặc nghiêng. Nếu chúng ta vẽ một góc giữa hai điểm bất kỳ trên đường thẳng, chúng ta sẽ luôn nhận được một độ 180.
Đường thẳng là hình được tạo thành khi hai điểm A ( x 1 , y 1 ) và B ( x 2 , y 2 ) nối với nhau với khoảng cách ngắn nhất giữa chúng và các đầu của đoạn thẳng kéo dài đến vô cùng.
Trong hình bên dưới, một đường thẳng nối hai điểm A và B.

Các đường thẳng có thể có nhiều loại khác nhau. Nói chung, các đường thẳng được phân loại dựa trên sự liên kết của chúng. Sự liên kết của chúng đề cập đến góc mà chúng tạo thành với trục x hoặc trục y. Theo sự liên kết của các đường thẳng, chúng có các loại sau:
– Đường kẻ ngang
– Đường thẳng đứng
– Đường xiên hoặc nghiêng
2. Vị trí tương đối của đường thẳng và đường tròn:
Một đường thẳng có thể:
– Cắt đường tròn tại hai điểm và đi qua tâm của nó;
– Cắt đường tròn tại hai điểm và không đi qua tâm của nó;
– Chạm vào vòng tròn;
– Không có điểm chung với đường tròn.
Vị trí tương đối của đường thẳng và đường tròn như vậy phụ thuộc vào hệ thức giữa bán kính của đường tròn và khoảng cách từ tâm của đường tròn đến đường thẳng.
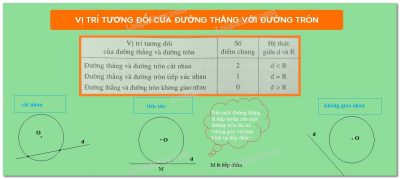
3. Đường thẳng là cát tuyến đối với đường tròn:
Đường thẳng và đường tròn có hai điểm chung nếu khoảng cách từ tâm của đường tròn đến đường thẳng nhỏ hơn đường kính của đường tròn. d<r
Cát tuyến đối với đường tròn là đường thẳng đi qua đường tròn.
Như vậy Đường thẳng có hai điểm chung với một đường tròn gọi là cát tuyến.
4. Đường cắt trùng với đường kính và đi qua tâm của đường tròn:
Nếu đường thẳng đi qua tâm đường tròn thì cắt đường tròn tại hai điểm: hai đầu đường kính nằm trên đường thẳng này.
Một đường thẳng đi qua tâm đường tròn nếu khoảng cách giữa tâm đường tròn này và đường thẳng bằng 0:
d=0
5. Đường thẳng là tiếp tuyến của đường tròn:
Nếu khoảng cách từ tâm của đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng và đường tròn chỉ có một điểm chung.
Như vậy, Đường thẳng chỉ có một điểm chung với đường tròn và vuông góc với bán kính được gọi là tiếp tuyến của đường tròn.
6. Đường thẳng và đường tròn không có điểm chung:
Nếu khoảng cách từ tâm của đường tròn đến đường thẳng lớn hơn bán kính của đường tròn thì đường thẳng và đường tròn sẽ không có điểm chung. d>r
Ở đâu:
d – khoảng cách từ tâm đường tròn đến đường thẳng (khoảng cách từ một điểm đến một đường thẳng được đo bằng độ dài đường vuông góc kẻ từ điểm này đến đường thẳng);
r − bán kính của hình tròn;
O – tâm của một vòng tròn.
Kết luận:
Định lý 1: Đường kính của đường tròn chia đôi dây cung vuông góc với dây cung đó.
Định lý 2 (ngược lại với Định lý 1): Nếu đường kính của đường tròn vuông góc với dây cung thì nó sẽ chia dây cung thành hai phần bằng nhau.
Hệ quả 1 : Nếu khoảng cách từ tâm của đường tròn đến đường cát tuyến nhỏ hơn độ dài bán kính của đường tròn thì đường thẳng cắt đường tròn tại hai điểm.
Hệ quả 2: Các dây cung của một đường tròn cách đều tâm một khoảng bằng nhau.
Định lý 3: Tiếp tuyến vuông góc với bán kính vẽ tiếp điểm.
Hệ quả 3 : Nếu khoảng cách từ tâm của đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến.
Hệ quả 4 : Nếu khoảng cách từ tâm của đường tròn đến đường thẳng lớn hơn bán kính của đường tròn thì đường thẳng đó không cắt đường tròn.
Định lý 4: Các đoạn tiếp tuyến của đường tròn vẽ từ một điểm thì bằng nhau và tạo các góc bằng nhau với đường thẳng đi qua điểm đó và tâm của đường tròn.
7. Câu hỏi bài tập:
7.1. Bài toán cấp độ 1:
1) Làm thế nào để một đường thẳng và một đường tròn nằm trên một mặt phẳng?
2) Đường thẳng có ba điểm chung với đường tròn được không?
3) Tiếp tuyến của đường tròn đi qua một điểm nằm trên đường tròn phải vẽ như thế nào?
4) Đường tròn đi qua một điểm có thể vẽ được bao nhiêu tiếp tuyến:
a) nằm trên đường tròn;
b) nằm bên trong hình tròn;
c) nằm bên ngoài hình tròn?
5) Cho đường tròn ω(O; r) và một điểm A nằm bên trong đường tròn. Có bao nhiêu giao điểm: a) Đoạn thẳng OA; b) tia OA; c) đoạn OA?
6) Làm thế nào để chia đôi dây cung của một vòng tròn?
7) Điều gì xác định vị trí của các vòng tròn?
8) Có đúng hai đường tròn cắt nhau tại ba điểm không?
9) Các hình tròn được sắp xếp như thế nào nếu:
a) khoảng cách giữa tâm các đường tròn bằng tổng các bán kính của chúng;
b) khoảng cách giữa tâm của các đường tròn nhỏ hơn tổng các bán kính của chúng;
c) khoảng cách giữa các tâm lớn hơn tổng hai bán kính;
d) khoảng cách giữa tâm các đường tròn bằng không.
10) Ba trường hợp sắp xếp lẫn nhau của hai đường tròn, đường tròn đồng tâm thuộc trường hợp nào sau đây?
11) Tên đường thẳng đi qua tiếp tuyến của các đường tròn là gì?
7.2. Bài toán cấp độ 2:
1. Tìm độ dài của hai đoạn dây cung mà đường kính của đường tròn chia đôi nó, nếu chiều dài của dây là 16 cm và đường kính vuông góc với nó.
2. Tìm chiều dài của dây cung nếu đường kính vuông góc với nó và một trong các đoạn bị cắt bởi đường kính từ nó là 2 cm.
3. Dựng hai đường tròn có bán kính lần lượt là 2 cm và 4 cm, khoảng cách giữa hai tâm bằng không.
4. Vẽ hai đường tròn có bán kính khác nhau (3 cm và 2 cm) sao cho chúng tiếp xúc với nhau. Đánh dấu khoảng cách giữa các tâm của chúng bằng một đường thẳng. Xem xét các lựa chọn của bạn.
5. Dựng đường tròn bán kính 3 cm và một đoạn thẳng cách tâm đường tròn một đoạn 4 cm.
6. Dựng đường tròn bán kính 4 cm và một đoạn thẳng cách tâm đường tròn một đoạn 2 cm.
7. Hai hình tròn tiếp xúc nhau. Bán kính của hình tròn lớn là 19 cm và bán kính của hình tròn nhỏ hơn là 4 cm. Tìm khoảng cách giữa tâm của các đường tròn.
8. Hai hình tròn tiếp xúc nhau. Bán kính của hình tròn lớn là 26 cm và bán kính của hình tròn nhỏ nhỏ hơn 2 lần. Tìm khoảng cách giữa tâm của các đường tròn.
9. Lấy hai điểm D và F sao cho DF = 6 cm . Vẽ hai đường tròn (D, 2cm) và (F, 3 cm). Hai vòng tròn này có vị trí như thế nào? Đưa ra một kết luận.
10. Khoảng cách giữa hai điểm BUT và AT bằng 7 cm Vẽ đường tròn có tâm là BUT và AT , có bán kính lần lượt là 3 cm và 4 cm . Các vòng tròn được sắp xếp như thế nào? Đưa ra một kết luận.
11. Giữa hai đường tròn đồng tâm có bán kính lần lượt là 4 cm và 8 cm, có một đường tròn thứ ba sao cho tiếp xúc với hai đường tròn thứ nhất. Bán kính của vòng tròn này là gì?
12. Các đường tròn có bán kính lần lượt là 6 cm và 2 cm cắt nhau. Hơn nữa, vòng tròn lớn hơn đi qua tâm của vòng tròn nhỏ hơn. Tìm khoảng cách giữa tâm của các đường tròn.
13. Vòng tròn chạm bên ngoài. Bán kính hình tròn bé là 3 cm, bán kính hình tròn lớn là 5 cm. Khoảng cách giữa các trung tâm là gì?
14. Vị trí tương đối của hai đường tròn là bao nhiêu nếu khoảng cách giữa các tâm là 4 và bán kính là 11 và 7:
15. Có thể nói gì về vị trí tương đối của đường thẳng và đường tròn nếu đường kính của đường tròn là 7,2 cm và khoảng cách từ tâm của đường tròn đến đường thẳng là 0,4 dm
16. Cho biết số điểm chung của đường thẳng và đường tròn nếu:
a) khoảng cách từ đường thẳng đến tâm của hình tròn là 6 cm và bán kính của hình tròn là 6,05 cm;
b) khoảng cách từ đường thẳng đến tâm của hình tròn là 6,05 cm và bán kính của hình tròn là 6 cm;
c) khoảng cách từ đường thẳng đến tâm hình tròn là 8 cm, bán kính hình tròn là 16 cm.
17. Tìm độ dài của dây cung nếu đường kính vuông góc với nó và một trong các đoạn bị cắt bởi đường kính từ nó là 2 cm.




