Tứ diện là gì? Tứ diện đều là gì? Công thức tính và bài tập?

1. Tứ diện là gì?

Trong hình học, tứ diện còn được gọi là hình chóp tam giác, là một khối đa diện gồm bốn mặt tam giác, sáu cạnh thẳng và bốn góc ở đỉnh. Khối tứ diện là khối đơn giản nhất trong số các khối đa diện lồi thông thường và là khối duy nhất có ít hơn 5 mặt.

Hình tứ diện là một loại hình chóp, là hình đa diện có đáy là đa giác phẳng và các mặt tam giác nối đáy với một điểm chung. Trong trường hợp tứ diện, đáy là một hình tam giác (bất kỳ mặt nào trong số bốn mặt đều có thể được coi là đáy), do đó, tứ diện còn được gọi là “hình chóp tam giác”.

Đối với bất kỳ tứ diện nào cũng tồn tại một mặt cầu (được gọi là mặt cầu ngoại tiếp ) trên đó có tất cả bốn đỉnh và một mặt cầu khác (mặt cầu trong ) tiếp xúc với các mặt của tứ diện

2. Tứ diện đều là gì?

Tứ diện đều là tứ diện có bốn mặt đều là tam giác đều. Nó là một trong năm chất rắn Platonic thông thường , đã được biết đến từ thời cổ đại.

Trong một tứ diện đều, tất cả các mặt đều có cùng kích thước và hình dạng (đồng dạng) và tất cả các cạnh đều có cùng độ dài.

Năm tứ diện được đặt phẳng trên một mặt phẳng, với các điểm 3 chiều cao nhất được đánh dấu là 1, 2, 3, 4 và 5.

Một mình tứ diện đều không xếp thành ô (lấp đầy khoảng trống), nhưng nếu xen kẽ với khối bát diện đều theo tỷ lệ hai tứ diện trên một bát diện, chúng tạo thành tổ ong lập phương xen kẽ , đó là một ô xếp xen kẽ. Một số tứ diện không đều, bao gồm tứ diện Schläfli và tứ diện Hill , có thể xếp thành hình khối .

Tứ diện đều là đối ngẫu, nghĩa là đối ngẫu của nó là một tứ diện đều khác. Hình ghép bao gồm hai tứ diện kép như vậy tạo thành một bát diện hình sao hoặc bát diện hình sao.

Hình tứ diện là một hình chóp đều có bốn mặt là hình tam giác. Điều này có nghĩa là chúng ta có thể tính thể tích của nó bằng cách nhân diện tích đáy của nó với chiều cao của tứ diện và chia cho ba. Ngoài ra, diện tích bề mặt của nó được tính bằng cách cộng diện tích của bốn mặt tam giác.

Sau đây, chúng ta sẽ tìm hiểu về các công thức tính thể tích và diện tích xung quanh của một tứ diện. Chúng ta sẽ học cách rút ra các công thức này và sẽ sử dụng chúng để giải một số bài tập thực hành.

3. Cách tìm thể tích của khối tứ diện:

Vì tứ diện là một hình chóp tam giác nên chúng ta có thể tính diện tích của nó bằng cách nhân diện tích đáy của nó với chiều dài của nó và chia cho 3.

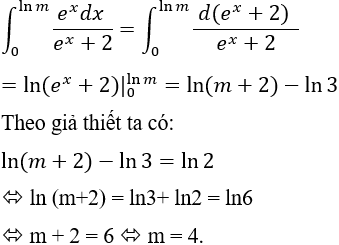
Chứng minh công thức tính thể tích khối tứ diện:

Công thức tính thể tích của khối tứ diện ABCD sẽ là như sau:

V = ⅓ S_BCD . AH

(Thể tích tứ diện ABCD bằng 1 phần 3 diện tích mặt đáy nhân với chiều cao của khối tứ diện).

Công thức tính thể tích của khối tứ diện SABC sẽ là như sau:

V = ⅓ B . h

(Thể tích của khối chóp bằng 1 phần 3 nhân với diện tích mặt đáy và chiều cao của khối chóp).

Đáy của một tứ diện là một tam giác đều và chúng ta biết rằng diện tích của bất kỳ tam giác nào cũng bằng 1/ 2 độ đài đáy nhân với chiều cao. Sau đó chúng ta có:

A_b = ½ a.h

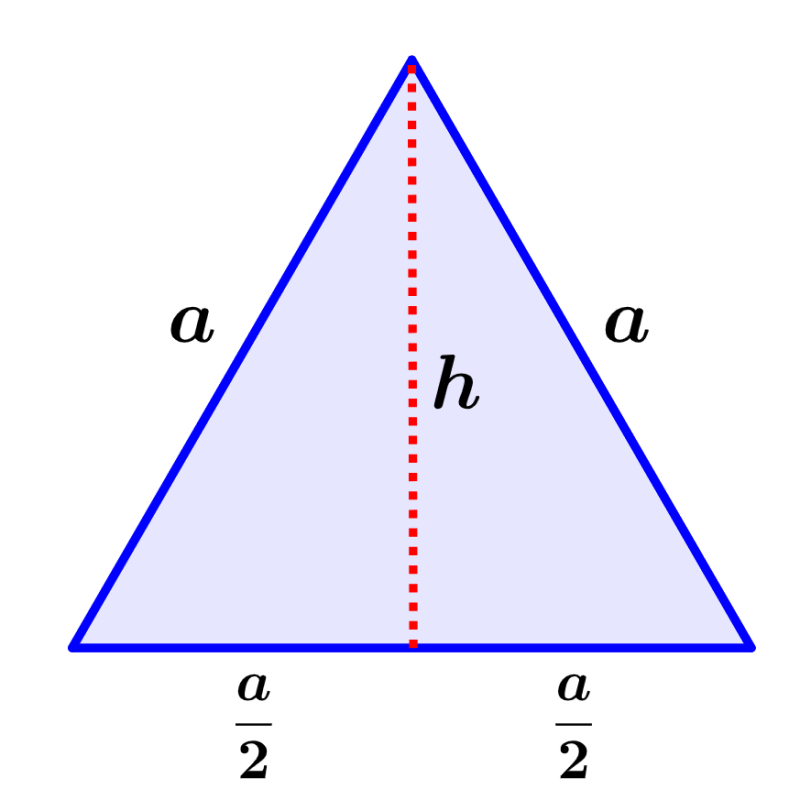
Công thức tính nhanh thể tích tứ diện đều cạnh a

Cho tứ diện đều ABCD cạnh a. từ A kẻ AH là đường cao của hình chóp A.BCD, H thuộc (BCD) thì H sẽ là tâm của tam giác đều BCD. Ta suy ra:

– Chiều cao của hình chóp A.BCD đều cạnh a là

– Thể tích khối tứ diện đều cạnh a là: 

Chứng minh:

Giả sử ABCD là khối tứ diện đều cạnh a. G là trọng tâm tam giác BCD (hình trên). Ta có:

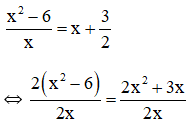
4. Cách tìm diện tích bề mặt của tứ diện:

Vì tứ diện đều là hình chóp tam giác nên cả bốn mặt của chúng đều bằng nhau. Điều này có nghĩa là tất cả các khuôn mặt của họ có hình dạng và kích thước giống nhau. Do đó, chúng ta có thể tính diện tích bề mặt nếu chúng ta biết diện tích của một trong các mặt của tứ diện.

Điều này có nghĩa là chúng ta có:

A_{s =} 4A_t

ở đây , A_s ​là diện tích bề mặt của tứ diện và At ​là diện tích của một trong các mặt tam giác.

Bây giờ, chúng ta có thể tính diện tích của một trong các mặt của một tứ diện là các tam giác đều. Do đó, chúng tôi sử dụng công thức cho diện tích của một tam giác đều :

trong đó a là độ dài của một trong các cạnh.

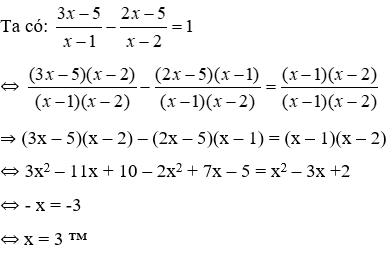
nơi mà  nó phải.

Bài tập 1: Hãy tính thể tích khối tứ diện đều ABCD biết:

a) cạnh AB = 4 cm

b) cạnh CD = 6 cm

c) cạnh BD = 3 cm

Hướng dẫn giải

Áp dụng công thức tính thể tích tứ diện đều cạnh a:  

a) Vì ABCD là tứ diện đều nên các cạnh có độ dài bằng nhau: BC = CD = DA = BD = AC = AB = 4 cm nên  a= 4 (cm). Khi đó thể tích ABCD là: V = 7,54 cm3

b) Vì là tứ diện đều nên AB = BC = DA = BD = AC = CD = 6 cm nên a= 6 (cm). Khi đó thể tích ABCD là: V = 25,46 cm3

c) Vì là tứ diện đều nên AB = BC = CD = DA = AC = BD = 3 cm nên a = 3 (cm). Khi đó thể tích ABCD là: V = 3,18 cm3

Bài tập 2: Cho hình chóp đều S.ABCD (đáy là hình vuông), đường SA vuông góc với mặt phẳng (ABCD). Xác định hình chóp này có mặt đối xứng nào.

Hướng dẫn giải:

Ta có: BD vuông góc với AC, BD vuông góc với SA.

Từ đó suy ra, BD vuông góc với (SAC) => (SAC) là mặt phẳng trung trực của BD.

Ta kết luận rằng, (SAC) là mặt đối xứng của hình chóp và đây là mặt phẳng duy nhất.

Bài tập 3: Tìm số mặt phẳng đối xứng của hình tứ diện đều.

Hướng dẫn giải: 

Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện. Vì vậy, hình tứ diện đều sẽ có 6 mặt phẳng đối xứng.

Một số bài tập tự giải:

Câu hỏi 1: Khối chóp tứ diện đều cạnh a có thể tích bằng:

Câu hỏi 2: Số mặt phẳng đối xứng của hình tứ diện đều là:

A. 4 mặt phẳng

B. 6 mặt phẳng

C. 8 mặt phẳng

D. 10 mặt phẳng

Câu hỏi 3: Cho hình chóp tam giác đều S.ABC có cạnh đáy a và cạnh bên bằng . Tính thể tích khối chóp S.ABC.

Câu hỏi 4: Cho tứ diện đều ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. tính thể tích của khối chóp A.GBC.

A. V = 4

B. V = 5

C. V = 3

D. V = 6

Câu hỏi 5: Trung điểm các cạnh của một tứ diện đều tạo thành:

A. Các đỉnh của một hình hai mươi mặt đều.

B. Các đỉnh của một hình mười hai mặt đều.

C. Các đỉnh của một hình bát diện đều.

D. Các đỉnh của một hình tứ diện.

Câu hỏi 6: Cho tứ diện đều ABCD cạnh a. Tính góc giữa AB và CD?

Câu hỏi 7: Cho ABCD là tứ diện đều, cạnh a. Kéo dài BC 1 đoạn CE = a. Kéo dài BD 1 đoạn DF = a. M là trung điểm của AB.

a. Tìm thiết diện của tứ diện với mặt phẳng (MEF).

b. Tính diện tích của thiết diện theo a.

Câu hỏi 8: Cho tứ diện đều ABCD có canh 2a. Tính thể tích khối tứ diện ABCD theo a

Câu hỏi 10: Cho tứ diện đều ABCD có thể tích bằng 1. Tìm độ dài các cạnh của tứ diện

Bài tập trắc nghiệm