Trung bình cộng là gì? Cách tính trung bình cộng chuẩn

1. Trung bình cộng là gì?

Theo toán học, trung bình cộng được hiểu là tỉ số giữa tổng giá trị của tập hợp số đó và toàn bộ các phân tử có trong tập hợp đó hoặc thương giữa tổng các số hạng trong dãy số đã cho với những số hạng vừa lấy tổng.

Hiểu một cách đơn giản về khái niệm trung bình cộng là tổng các số hạng có trong dãy số đã cho CHIA tổng các số hạng.

Còn trong thống kê, trung bình cộng đơn giản là một đại lượng mô tả thống kế, được tính ra bằng cách lấy tổng giá trị của toàn bộ các quan sát trong tập chia cho số lượng các quan sát trong tập. 

2. Ý nghĩa của trung bình cộng là gì?

Trong các quan hệ chung, số trung bình cộng mang ý nghĩa cho sự công bằng. Hiện nay, số trung bình cộng được áp dụng rất nhiều trong thực tế của cuộc sống. Dựa vào số trung bình cộng, bạn sẽ có thể so sánh hay tính toán các khía cạnh trong đời sống và công việc mà có liên quan đến con số. Chẳng hạn, số trung bình cộng có những ý nghĩa sau:  

– Mức thu nhập trung bình của 1 người/1 tháng

– Thu nhập bình quân đầu người của một quốc gia để đánh giá sức mạnh kinh tế của một đất nước và có chiến lược phát triển kinh tế phù hợp.

– Dùng để tính tuổi thọ trung bình của toàn bộ dân số của một quốc gia tại một thời điểm nhất định. Công thức có thể tính tuổi trung bình trên phạm vi lớn như một quốc gia hoặc một khu vực khi có đầy đủ các số liệu thống kê. Tuy nhiên, việc tính toán với số lượng lớn đòi hỏi các nhà nghiên cứu phải sử dụng thuật toán.

– Những khía cạnh khác

Và đặc biệt trong toán học, số trung bình cộng sẽ được người ta dùng để làm đại diện cho một “dấu hiệu”, nhất là trong trường hợp so sánh các dấu hiệu cùng loại. 

3. Công thức tính trung bình cộng chuẩn:

3.1. Công thức tính trung bình cộng:

Muốn tìm số trung bình cộng của nhiều số, ta tính tổng các số đó rồi chia tổng đó cho số các số hạng.

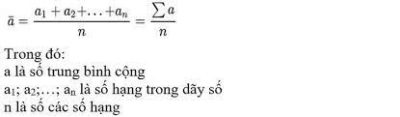
Lưu ý: Các số trong dãy số tính trung bình cộng phải là số thực chứ không được là biến số.

Khi tính trung bình cộng, các số trong dãy số đó phải là số thực, không được là các biến số. Cụ thể, để tìm trung bình cộng của nhiều số, bạn có thể thực hiện theo cách sau: 

Hãy tiến hành cộng tất cả những số xuất hiện trong dãy số để tìm ra số tổng. Nếu dãy số có nhiều số thì bạn nên sử dụng máy tính cầm tay để tính và đưa ra một con số tổng chính xác nhất. 

Tiếp theo, bạn đếm xem số đó có bao nhiêu số hạng và chia tổng các số vừa tìm được cho số hạng đó. Nếu bạn thấy những số hạng giống nhau thì tuyệt đối không được tính gộp mà phải đếm đầy đủ số hạng đó. Chẳng hạn, tổng các số là 50 với 5 số hạng thì bạn lấy 50:5 = 10, đây chính là trung bình cộng của dãy số. 

3.2. Phương pháp giải toán trung bình cộng:

Muốn tính số trung bình cộng của nhiều số, ta làm như sau:

Bước 1: Xác định số lượng các số hạng có trong bài toán;

Bước 2: Tính tổng các số hạng vừa tìm được;

Bước 3: Trung bình cộng = “Tổng các số hạng” chia “số các số hạng có trong bài toán”;

Bước 4: Kết luận.

Ví dụ 1. Tìm trung bình cộng của hai số 2 và 18.

Ta có tổng của hai số là 2+18=20.

Số các số hạng là: 2.

Trung bình cộng của hai số đã cho là: 20:2=10.

Ví dụ 2. Tìm trung bình cộng của các số sau: 6,9,13,28.

Tổng của các số là: 6+9+13+28=56;

Số các số hạng là: 4;

Trung bình cộng của bốn số đã cho là: 56:4=14.

3.3. Quy tắc tìm số trung bình cộng:

Số trung bình cộng của một dấu hiệu được tính từ bảng tần số theo cách sau:

– Nhân từng giá trị với tần số tương ứng

– Cộng tất cả các tích vừa tìm được

– Chia tổng đó cho các giá trị (tức tổng các tần số).

4. Những nguyên tắc khi sử dụng số trung bình cộng:

4.1. Những nguyên tắc cần chú ý:

– Số trung bình cộng chỉ được tính trong một tổng thể gồm những đơn vị có chung tính chất, thuộc một loại hình,…

– Khi so sánh hai tổng thể cùng loại, cùng quy mô thì bạn phải dùng số bình quân tổ bổ sung cho số bình quân chung.

– Sử dụng dãy số phân phối để bổ sung cho số bình quân chung. Nguyên tắc này sẽ được áp dụng cho trường hợp bạn cần so sánh 2 đối tượng cùng loại nhưng có kết cấu tổng thể khác nhau.

4.2. Những điểm hạn chế của số trung bình cộng:

Mặc dù trung bình cộng được áp dụng trong rất nhiều các trường hợp khác nhau. Tuy nhiên, giá trị trung bình cộng trong một số trường hợp sẽ không thật sự đem đến một cách hiệu quả tốt nhất.

Chẳng hạn, trong một số trường hợp bạn cần tính trung bình của một nhóm khoảng 10 người nhưng số trung bình 9 người giao động từ 10 đến 12, tuy nhiên lại có 1 người có số tương ứng là 60. Điều này khiến điểm trung bình bằng 16, đây là con số hoàn toàn không đại diện cho nhóm bởi một cá nhân có sự khác biệt quá lớn. 

Chính vì vậy, trong từng trường hợp cụ thể thì bạn nên áp dụng công thức tính sao cho phù hợp nhất. Trong một số trường hợp, bạn có thể áp dụng giới hạn trung binh 10 thay vì trung bình cộng. 

Nhìn chung, trung bình cộng là một thuật toán nhằm tìm ra một con số trung bình trong một dãy số khác nhau. Từ đó giúp cho người tìm có thể biết được mức điểm chung của một nhóm ở cao hay thấp và đưa ra những giải pháp phù hợp nhất.

5. Những dạng bài tính trung bình cộng:

5.1. Bài tập dạng 1: Cho dãy số, yêu cầu tính trung bình cộng:

Bài tập 1: Cho dãy số gồm các chữ số: 3, 5, 9, 10, 13. Tính số trung bình cộng

Gợi ý đáp án bài tập 1:

Tổng của các số là: 3+5+9+10+13 = 40

Dãy số trên có 5 số hạng

=> Trung bình cộng của dãy số trên = tổng : số các số hạng = 40: 5 = 8

Bài tập 2: Khối 4 của một trường tiểu học có  3 lớp 4A, 4B, 4C. Lớp 4A có tổng 19 học sinh, lớp 4B có 21 học sinh và lớp 4C là 23 học sinh. Hỏi trung bình mỗi lớp có bao nhiêu hoc sinh?

Gợi ý đáp án bài tập 2:

Số của số hạng ở đây là 3 vì có 3 lớp 4A, 4B, 4C

Tổng số học sinh của 3 lớp là 19+21+23 = 63

=> Trung bình số học sinh của khối 4 là: 63:3 = 21 (học sinh).

5.2. Dạng 2: Biết số trung bình cộng, biết số hạng, tìm tổng các số đó:

Để tìm được đáp án cho các bài tập dạng này bạn lấy trung bình cộng đã biết nhân với số các số dạng.

Bài tập 1: Biết tuổi trung bình của 30 học sinh lớp 4 là 9 tuổi. Nếu tính cả cô giáo dạy toán thì tuổi trung bình của 30 học sinh là 10 tuổi. Hỏi cô giáo dạy toán bao nhiêu tuổi?

Gợi ý đáp án bài tập 1:

Tổng số tuổi của 30 học sinh: 9×30 = 270 tuổi

Số người trong lớp là 30 + 1 =31 (người)

Tổng số tuổi của 31 người là 10 x 31 = 310 (tuổi)

=> Số tuổi của cô giáo dạy toán là 310 – 270 = 40 tuổi.

Bài tập số 2: Trung bình cộng của tám số là 12, do thêm số thứ 9 nên trung bình cộng là 13. Tìm số thứ 9 ?

Gợi ý lời giải bài tập 2:

Tổng của tám số lúc đầu: 12 x 8 = 96

Tổng của chín số: 13 x 9 = 117

=> Số thứ chín sẽ là 117 – 96 = 21.

Diện tích hình thoi là gì? Công thức tính chu vi, diện tích hình thoi

5.3. Dạng 3: Tính trung bình cộng của dãy số cách đều:

Để tìm được đáp án cho dạng bài tính trung bình cộng này bạn thực hiện như sau:

Tìm trung bình cộng của số đầu, số cuối

Khi thấy dãy số có các số hạng là 1 số lẻ, thì số trung bình cộng sẽ là số ở chính giữa dãy số đó. Còn nếu là số chẵn thì số trung bình cộng sẽ là 1/2 tổng của 2 số đầu và số cuối. Nếu dãy số đã cho có 1 số bằng trung bình của các số còn lại thì số đó sẽ bằng trung bình cộng của các số đã cho.

Bài tập số 1: Trung bình cộng của 10 số là 50. Nếu lấy số thứ nhất cộng với 1, số thứ hai cộng với 2,…số thứ 10 cộng với 10 thì trung bình cộng của 10 số mới là bao nhiêu?

Gợi ý đáp án bài tập 1:

Tổng tăng thêm là 1 + 2 + 3 +….+10 = 50

Trung bình cộng tăng thêm sẽ là: 55 : 10 = 5,5

=> Trung bình cộng số mới là 50 + 5,5 = 55,5

Bài tập số 2: Cho dãy số 2, 4, 6, 8, 10, 12. Trong đó, có 4 số có trung bình cộng bằng 8, tính trung bình cộng của các số còn lại?

Gợi ý đáp án bài tập 2:

Tổng 6 số là: 2 + 4 + 6 +8 + 10+ 12 = 42

Tổng 4 số là: 4 x 8 = 32

Tổng 2 số còn lại: 42 – 32 = 10

=> Trung bình cộng của 2 số còn lại là 10 : 2 = 5

6. Cách tính trung bình cộng trong excel:

Trong excel, bạn có thể sử dụng các hàm như Average hoặc Sum để tính trung bình cộng của một dãy số. Để các bạn tiện theo dõi và hiểu rõ hơn về cách tính Trung bình cộng trong excel, mình sẽ đưa ra ví dụ cụ thể như sau: 

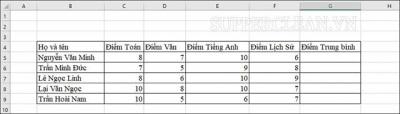
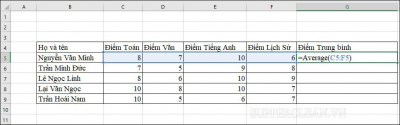
Yêu cầu: Hãy tính điểm trung bình của các bạn học sinh trong danh sách dưới đây:

6.1. Cách 1: Tính trung bình cộng theo từng giá trị:

Áp dụng vào ví dụ minh họa trên: 

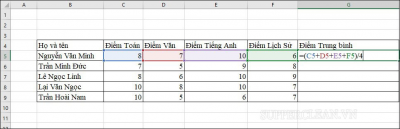
Tại ô G5 nhập công thức: =(C5 + D5 + E5 + F5)/4  rồi nhấn Enter. 

Để tính trung bình của các bạn tiếp theo, bạn chỉ cần để con chuột vào ô chứa kết quả rồi kéo biểu tượng dấu cộng xuống để sao chép công thức. 

6.2. Cách 2: Tính trung bình cộng bằng hàm Sum:

Cách làm này khá đơn giản, dễ thực hiện và nhanh chóng. Cách làm số 2 khá giống với cách đầu tiên nhưng khác ở chỗ là mình sẽ dùng hàm Sum để tính tổng. 

Áp dụng vào ví dụ minh họa trên: 

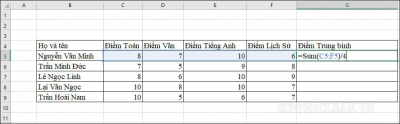
Tại ô G5 nhập công thức: =Sum(C5:F5)/4 hoặc =Sum(C5,D5,E5,F5)/ 4 rồi nhấn enter. 

Để tính trung bình của các bạn tiếp theo, bạn chỉ cần để con chuột vào ô chứa kết quả rồi kéo biểu tượng dấu cộng xuống để sao chép công thức. 

Lưu ý: Phải dùng dấu ngoặc tròn để kết thúc tổng trước rồi mới nhấn phép chia.

6.3. Cách 3: Cách tính trung bình cộng bằng hàm Average:

Cách tính này rất đơn giản, dễ thực hiện và không tốn nhiều thời gian. 

Cú pháp thực hiện: 

=Average (number1, number2,…. numbern)

Lưu ý: Dấu ngăn cách giữa các number có thể là dấu “;” hoặc dấu “,” tùy theo thiết lập của máy. Vì vậy bạn cần phải xem kỹ máy tính để tránh hàm nhập bị lỗi. Hoặc nếu các giá trị cần tính trung bình liên tiếp nhau thì bạn chỉ cần nhập hàm rồi kéo từ giá trị đầu tiên đến giá trị cuối cùng là được. 

Áp dụng vào ví dụ minh họa trên: 

Tại ô G5 nhập công thức: =Average(C5:F5) hoặc =Average(C5,D5,E5,F5) rồi nhấn Enter. 

Để tính trung bình của các bạn tiếp theo, bạn chỉ cần để con chuột vào ô chứa kết quả rồi kéo biểu tượng dấu cộng xuống để sao chép công thức.