Tổng hợp kiến thức và các dạng bài tập Toán 7 đầy đủ

1. Tổng hợp kiến thức Toán lớp 7 đại số: 

1. Số hữu tỉ: Số hữu tỉ là số viết được dưới dạng phân số a/b với a, b ∈ Z, b ≠ 0

Kí hiệu tập hợp số hữu tỉ: Q

2. Số thập phân hữu hạn và số thập phân vô hạn tuần hoàn

– Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn.

– Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.

3. Các phép toán thực hiện trong tập hợp số hữu tỉ Q

+) Cộng, trừ hai số hữu tỉ: Đưa số hữu tỉ về dạng phân số cùng mẫu dương

* Cộng hai số hữu tỉ:

* Trừ hai số hữu tỉ:

– Chú ý: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

Với mọi x, y, z ∈ Q: x + y = z ⇒ x = z – y.

* Nhân hai số hữu tỉ:

* Chia hai số hữu tỉ:

4. Giá trị tuyệt đối của một số hữu tỉ x.

+) Tính chất: Với mọi x ∈ Q thì |x| ≥ 0; |x| = |-x|; |x| ≥ x

5. Viết các công thức tính lũy thừa của một số hữu tỉ.

Quy ước: x¹ = x; x⁰ = 1 (x ≠ 0)

– Tích của hai luỹ thừa cùng cơ số: x^m . xⁿ = x^{m + n}

– Thương của hai luỹ thừa cùng cơ số: x^m : xⁿ = x^{m – n} (x ≠ 0, m ≥ n)

– Luỹ thừa của luỹ thừa: (x^m)ⁿ = x^m:n

– Luỹ thừa của một tích: (x . y)ⁿ = xⁿ . yⁿ

– Luỹ thừa của một thương:  (y ≠ 0)

6. Tỉ lệ thức

– Tỉ lệ thức là đẳng thức của hai tỉ số .

– Từ đẳng thức a . d = b . c ta có thể suy ra được các tỉ lệ thức sau:

7. Tính chất của dãy tỉ số bằng nhau.

– Tính chất của dãy tỉ số bằng nhau (với điều kiện các biểu thức có nghĩa)

8. Quy ước làm tròn số

Trường hợp 1: Nếu chữ số đầu tiên trong các chữ số bị bỏ đi nhỏ hơn 5 thì ta giữ nguyên bộ phận còn lại. Ví dụ, nếu số nguyên ban đầu là 123, ta thay các chữ số bị bỏ đi bằng các chữ số 0, kết quả là 100. Tuy nhiên, nếu số thập phân ban đầu là 1.23, ta thay các chữ số bị bỏ đi bằng các chữ số 0, kết quả vẫn là 1.23.

Trường hợp 2: Nếu chữ số đầu tiên trong các chữ số bị bỏ đi lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào chữ số cuối cùng của bộ phận còn lại. Ví dụ, nếu số nguyên ban đầu là 678, ta thay các chữ số bị bỏ đi bằng các chữ số 0 và cộng thêm 1 vào chữ số cuối cùng, kết quả là 680. Tuy nhiên, nếu số thập phân ban đầu là 6.78, ta thay các chữ số bị bỏ đi bằng các chữ số 0 và cộng thêm 1 vào chữ số cuối cùng, kết quả vẫn là 6.78.

9. Số vô tỉ. Căn bậc hai

– Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.

– Kí hiệu tập số vô tỉ: I

– Căn bậc hai của một số a không âm là một số x sao cho x² = a

– Số dương a có đúng hai căn bậc hai, một số dương kí hiệu là và một số âm kí hiệu là –

10. Số thực

– Số hữu tỉ và số vô tỉ được gọi chung là số thực

– Tập hợp số thực: R

Ta có: R = Q ∪ I

2. Tổng hợp kiến thức Toán lớp 7 hình học: 

1. Hai góc đối đỉnh

– Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

– Hai góc đối đỉnh thì bằng nhau:

2. Hai đường thẳng vuông góc

– Hai đường thẳng xx’, yy’ cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc và được kí hiệu là .

– Thừa nhận tính chất sau: Có một và chỉ một đường thẳng a’ đi qua điểm O và vuông góc với đường thẳng a cho trước.

3. Đường trung trực của đoạn thẳng

– Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.

– Khi xy là đường trung trực của đoạn thẳng AB ta cũng nói: Hai điểm A và B là đối xứng với nhau qua đường thẳng xy.

xy là đường trung trực của đoạn thẳng AB thì

4. Các góc tạo bởi một đường thẳng cắt hai đường thẳng:

Đường thẳng c cắt hai đường thẳng a, b và tạo thành các cặp góc:

– So le trong:

– Đồng vị:

– Trong cùng phía:

5. Hai đường thẳng song song

Hai đường thẳng song song là hai đường thẳng không có điểm chung. Điều này có nghĩa là chúng không giao nhau và không có điểm nào thuộc cả hai đường thẳng.

Để nhận biết hai đường thẳng song song, ta có thể sử dụng một dấu hiệu quan trọng. Nếu một đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau, thì ta có thể kết luận rằng đường thẳng a và b là hai đường thẳng song song với nhau.

Điều này có nghĩa là nếu ta có một đường thẳng cắt hai đường thẳng song song, thì các góc tạo thành bởi đường cắt và hai đường thẳng sẽ có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau.

Dấu hiệu này giúp chúng ta xác định một cách chính xác liệu hai đường thẳng có song song hay không, mà không cần xác định các điểm cắt của chúng.

Vì vậy, nếu ta tìm thấy một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau trong các góc tạo thành bởi đường cắt và hai đường thẳng, thì ta có thể kết luận rằng hai đường thẳng đó là song song với nhau.

 Kí hiệu: a // b

6. Tiên đề Ơ – clit về đường thẳng song song

+) Tiên đề: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

+) Tính chất: Nếu một đường thẳng cắt hai đường thẳng song song thì:

– Hai góc so le trong bằng nhau

– Hai góc đồng vị bằng nhau

– Hai góc trong cùng phía bù nhau

+) Bổ sung: Điều này có nghĩa là, khi một đường thẳng cắt hai đường thẳng song song, các góc mà nó tạo thành có một số tính chất đặc biệt. Hai góc so le trong (cùng nằm giữa hai đường thẳng song song) sẽ có giá trị bằng nhau. Tương tự, hai góc đồng vị (cùng nằm bên ngoài hai đường thẳng song song) cũng sẽ có giá trị bằng nhau. Ngoài ra, hai góc trong cùng phía (một nằm giữa hai đường thẳng song song và một nằm bên ngoài) sẽ có tổng giá trị bằng 180 độ.

+) Nếu a // b thì:

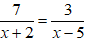
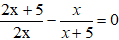
3. Bài tập vận dụng liên quan: 

Câu 1: Kết quả của phép tính 3⁶ . 3⁴  là:

A. 9¹⁰ 

B. 3²⁴                                

C. 3¹⁰                                

D. 27⁴⁸

Đáp án: C

Câu 2: Cho ba đường thẳng phân biệt a, b , c. Biết a $\perp$ c và b $\perp$ c, ta suy ra:

A. a và b cắt nhau.

B. a và b song song với nhau.

C. a và b trùng nhau.

D. a và b vuông góc với nhau.

Đáp án: B

Câu 3: Nếu 1 đường thẳng cắt 2 đường thẳng song song thì:

A. Hai góc trong cùng phía bù nhau

B. Hai góc đồng vị phụ nhau

C. Hai góc so le trong bù nhau

D. Cả 3 ý trên đều sai

Đáp án: A

Câu 4. Làm tròn số 0,345  đến chữ số thập phân thứ nhất

A. 0,35

B. 0,34

C. 0,3

D. 0,4

Đáp án: C

Câu 5. Tiên đề Ơclít được phát biểu:

“ Qua một điểm M nằm ngoài đường thẳng a ….”

A. Có duy nhất một đường thẳng đi qua M và song song với a.

B. Có hai đường thẳng song song với a.

C. Có ít nhất một đường thẳng song song với a.

D. Có vô số đường thẳng song song với a.

Đáp án: A

Câu 6.  Cho 3 đường thẳng a, b, c. Biết //  và c $\perp$ b. Khẳng định nào sau đây là đúng:

A. a $\perp$ b

B. a và b cùng vông góc với c

C. a // b

D. a và b cùng song song với c. 

Đáp án: A