Tổng hợp kiến thức và các dạng bài tập Toán 12 chi tiết để giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải các dạng bài tập phổ biến trong môn Toán lớp 12. Bộ tài liệu này cung cấp một cái nhìn tổng quan về các chủ đề quan trọng như đại số, hình học, giải tích...
Mục lục bài viết
1. Tổng hợp kiến thức và các dạng bài tập Toán 12 chi tiết phần đại số:

Lý thuyết và công thức chương đạo hàm

Lý thuyết và công thức chương đạo hàm

Lý thuyết và công thức chương đạo hàm

Lý thuyết và công thức chương đạo hàm

Lý thuyết và công thức chương đạo hàm

Lý thuyết về nguyên hàm

Lý thuyết về nguyên hàm

Lý thuyết về tích phân

Lý thuyết về tích phân

Lý thuyết về tích phân
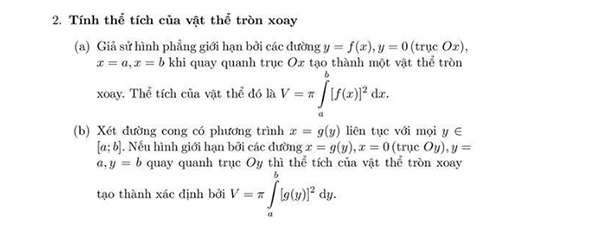
Lý thuyết về tích phân

Lý thuyết và công thức chương số phức

Lý thuyết và công thức chương số phức

Lý thuyết và công thức chương số phức
2.Tổng hợp kiến thức và các dạng bài tập Toán 12 chi tiết phần hình học:

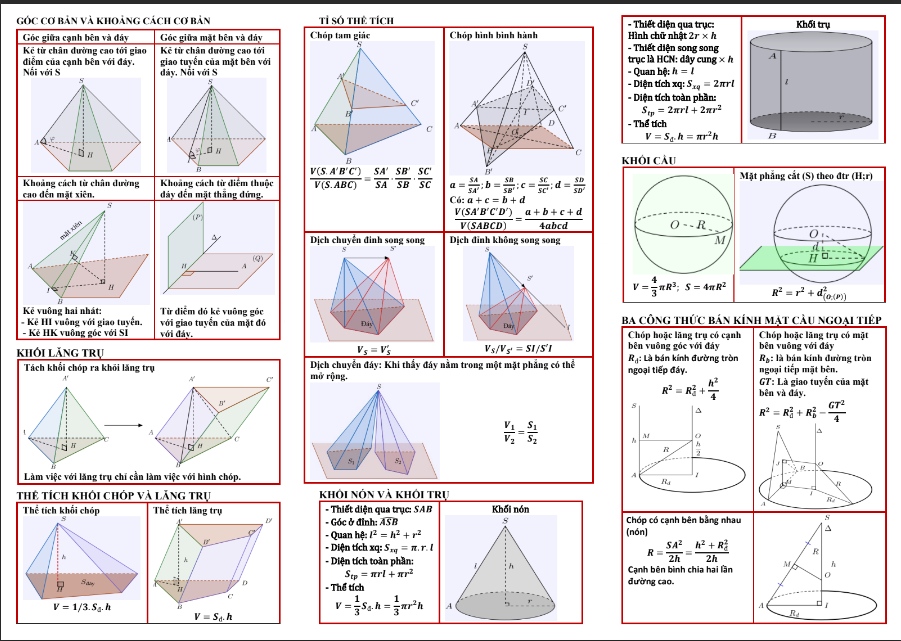


3. Một số dạng bài tập chi tiết:
Bài 1: Cho hàm số:
Cho hàm số:
a) Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
b) Với giá trị nào của m thì hàm số đạt cực đại tại x = 1?
Hướng dẫn làm bài:
a)
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua.
+) Với Khi đó, y’ không đổi dấu nếu
– Với điều kiện đó, ta có nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
Mặt khác,
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0, hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
Bài 2:
Một khu rừng có trữ lượng gỗ 4.105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?
Hướng dẫn làm bài:
Gọi trữ lượng gỗ ban đầu là V0, tốc độ sinh trưởng hằng năm của rừng là i phần trăm. Ta có:
– Sau 1 năm, trữ lượng gỗ là:
V1 = V0 + iV0 = V0(1 + i)
– Sau 2 năm, trữ lượng gỗ là:
V2 = V1 + iV1 = V1(1 + i) = V0(1 + i)2
………………
– Sau 5 năm, trữ lượng gỗ là
V5 = V0(1 + i)5
Thay V0 = 4.105 (m3), i = 4% = 0,04, ta được
V5 = 4.105 (1 + 0,04)5 = 4,8666.105 (m3).
Bài 3 (trang 50 SGK Hình học 12): Một hình chóp có tất cả các cạnh bên bằng nhau. Chứng minh rằng hình chóp đó nội tiếp được trong một mặt cầu (các đỉnh của hình chóp nằm trên mặt cầu).
Lời giải:
Cho hình chóp S.A1A2A3… An có các cạnh bên bằng nhau.
Gỉa sử I là hình chiếu vuông góc của S trên mặt đáy.
Ta có: SA1 = SA2 = SA3 = … = SAn
Suy ra ΔSIA1= ΔSIA2 = ΔSIA3 = … = ΔSIAn
Suy ra IA1 = IA2 = IA3 = … = IAn
Đa giác A1A2A3… An là một đa giác nội tiếp được trong một đường tròn tâm I bán kính IA, trục SI.
Trong mp(SAI), đường trung trực của SA1 cắt SI tại O, ta có:
OS = OA1 (1)
OA1 = OA2 = OA3 = … = OAn (2)
Từ (1) và (2) suy ra OS = OA1 = OA2 = OA3 = … = OAn
Vậy hình chóp S.A1A2A3…An nội tiếp được trong một mặt cầu.
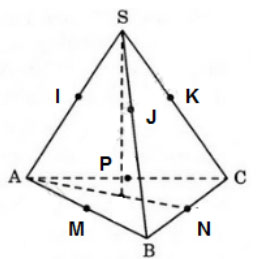
Bài 4 (trang 50 SGK Hình học 12): Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh bên SA, SB, SC. Mặt cầu này còn tiếp xúc với ba cạnh AB, BC, CA tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.
Lời giải:
Gọi M, N, P lần lượt là trung điểm của AB, BC, CA; I, J, K là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu.
Ta có: AM = AI và BM = BJ
Mà AM = BM nên AI = BJ
Mặt khác SI = SJ
Nên SI + AI = SJ + BJ
Vậy SA = SB (1)
Tương tự, ta có: SB = SC (2)
Từ (1) và (2) => SA = SB = SC (3)
Mặt khác BM = BN và CN = CP
Suy ra AB = 2BM = BC = 2CN = 2CP = CA
Khi đó ABC là tam giác đều (4)
Từ (3) và (4) suy ra S.ABC là hình chóp tam giác đều.
Bài 5 (trang 50 SGK Hình học 12): Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
a) Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH.
b) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao AH.
Lời giải:

Bài 6: Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1)
a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
b) Tìm góc giữa hai đường thẳng AB và CD
c) Tính độ dại đường cao của hình chóp A.BCD
Lời giải:

Bài 7: Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7)
a) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
b) Lập phương trình của mặt cầu (S).
c) Lập phương trình của mặt phẳng (α) tiếp xúc với mặt cầu (S) tại điểm A
Lời giải:
Bài 9: Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0)
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
b) Tính chiều cao AH của tứ diện ABCD.
c) Viết phương trình mặt phẳng (α) chứa AB và song song với CD.
Lời giải:

Bài 10: Cho hình chóp S.ABCD có đáy là hình thoi ABCD, AC cắt BD tại gốc tọa độ O. Biết A(2; 0; 0), B(0; 1; 0),S(0;0;2√2. Gọi M là trung điểm cạnh SC.
a) Viết phương trình mặt phẳng chứa SA và song song với BM.
b) Tính khoảng cách giữa hai đường thẳng SA và BM.
Hướng dẫn làm bài
a) Ta có C(-2; 0; 0) và M(−1;0;√2)
Gọi (α) là mặt phẳng chứa SA và song song với BM. Hai vecto có giá song song hoặc nằm trên (α) là SA→=(2;0;−2√2) và BM→=(−1;−1;√2)
Suy ra vecto pháp tuyến của (α) là: n→=(−2√2;0;−2) hay n→′=(√2;0;1)
Mặt phẳng (α) có phương trình: √2(x−2)+z=0 hay √2x+z−2√2=0
b) Ta có d(SA,BM)=d(B;(α))=|−2√2|/√2+1=2√2/√3
Vậy khoảng cách giữa hai đường thẳng SA và BM là 2√6/3
Bài 11: Cho mặt phẳng (P): 2x – 3y + 4z – 5 = 0 và mặt cầu (S):
x2 + y2 + z2 + 3x + 4y – 5z + 6 = 0
a) Xác định tọa độ tâm I và bán kính r của mặt cầu (S).
b) Tính khoảng cách từ tâm I đến mặt phẳng (P). Từ đó chứng minh rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn mà ta kí hiệu là (C). Xác định bán kính r’ và tâm H của đường tròn (C) .
Hướng dẫn làm bài:
a) (S) có tâm I(−3/2;−2;5/2) và có bán kính ![]()
b) d(I,(P))=|2.(−3/2)−3.(−2)+4.(5/2)−5|/√4+9+16=8/√29<√26/2
Vậy d(I, (P)) < r
Suy ra mặt phẳng (P) cắt mặt cầu (S) theo đường tròn tâm H bán kính r’.
H chính là hình chiếu vuông góc của I xuống mặt phẳng (P). Gọi Δ là đường thẳng qua I và vuông góc với (P). Ta có vecto chỉ phương của Δ là
a→Δ= n(P)→=(2;−3;4)
Phương trình tham số của Δ: x=−3/2+2t;y=−2−3t;z=5/2+4t
Δ cắt (P) tại H(−32+2t;−2−3t;52+4t). Ta có:
H∈(α)⇔2(−3/2+2t)−3(−2−3t)+4(5/2+4t)−5=0
⇔29t+8=0⇔t=−8/29
Suy ra tọa độ H(−3/2−16/29;−2+24/29;5/2−32/29) hay
Ta có r′2=r2−d2(I,(P))=26/4−64/29=249/58. Suy ra r′=√249/58