Đạo hàm là một khái niệm cơ bản trong giải tích, mô tả sự biến thiên của một hàm số tại một điểm cụ thể. Trong bài viết dưới đây mời bạn đọc hãy cùng chúng tôi tính đạo hàm cấp hai của các hàm số sau: y = cos^2x.
Mục lục bài viết
1. Tính đạo hàm cấp hai của các hàm số sau:
Tính đạo hàm cấp hai của các hàm số sau: y = cos^2x
A. 2cosx.sinx
B. -sin2x
C. -sinx
D. Tất cả đều sai
Đáp án: B. -sin2x
2. Đạo hàm là gì?
Trong toán học, đạo hàm (tiếng Anh: derivative) là một khái niệm cơ bản trong giải tích, mô tả sự biến thiên của một hàm số tại một điểm cụ thể. Đạo hàm được sử dụng để đo lường tốc độ thay đổi của hàm số tại một thời điểm xác định và có ứng dụng rất rộng trong nhiều lĩnh vực, như vật lý, kinh tế, và xác suất thống kê.
Đạo hàm còn có thể được hiểu là hệ số góc của tiếp tuyến tại một điểm trên đồ thị của hàm số. Tiếp tuyến là đường thẳng cắt qua đồ thị của hàm số tại một điểm, và đạo hàm chính là hệ số góc của tiếp tuyến đó. Nếu đạo hàm của hàm số tồn tại tại một điểm, thì nó cũng là xấp xỉ tuyến tính tốt nhất của hàm số gần với giá trị đã cho. Đạo hàm được sử dụng để xác định các đặc điểm quan trọng của hàm số, như điểm cực trị (cực đại hoặc cực tiểu) và điểm uốn (nơi hàm số thay đổi từ tăng đến giảm hoặc từ giảm đến tăng).
Vì tính chất này, đạo hàm thường được mô tả là “tốc độ thay đổi tức thời” của hàm số. Tốc độ thay đổi này phụ thuộc vào biến độc lập của hàm số, tức là giá trị mà hàm số phụ thuộc vào. Đạo hàm giúp chúng ta hiểu rõ hơn về sự biến thiên và xu hướng của hàm số, và có thể áp dụng để giải các bài toán thực tế trong nhiều lĩnh vực khác nhau. Ngoài ra, đạo hàm còn có thể được sử dụng để tìm điểm cực trị của hàm số, giúp chúng ta tìm ra điểm lớn nhất hoặc nhỏ nhất của hàm số trong một khoảng xác định.
Trong tự nhiên và khoa học, đạo hàm được sử dụng để mô hình hóa các quy luật và quy tắc tự nhiên. Ví dụ, trong lĩnh vực sinh học, đạo hàm được sử dụng để mô tả tốc độ sinh trưởng của một dân số hoặc sự biến đổi của một đặc điểm di truyền theo thời gian. Đạo hàm cũng là công cụ quan trọng trong xác suất thống kê, giúp tính toán xác suất và độ tin cậy trong các phân phối xác suất và mô hình thống kê.
Tóm lại, đạo hàm là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Nó giúp chúng ta hiểu rõ hơn về sự biến thiên và xu hướng của hàm số, từ đó áp dụng để giải quyết các vấn đề và bài toán trong nhiều lĩnh vực khác nhau. Đạo hàm là công cụ quan trọng trong việc phân tích và mô hình hóa các quy luật tự nhiên và quy tắc thống kê, đóng vai trò quan trọng trong sự phát triển và ứng dụng của toán học và khoa học.
3. Công thức tính đạo hàm lượng giác:
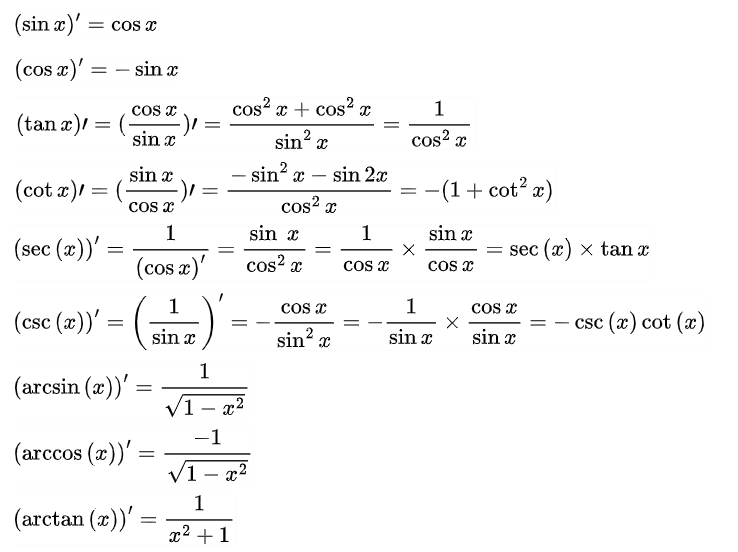
4. Ứng dụng của đạo hàm:
Đạo hàm là một công cụ quan trọng trong toán học và các lĩnh vực liên quan. Dưới đây là một số ứng dụng phổ biến của đạo hàm:
– Tìm điểm cực trị: Đạo hàm được sử dụng để tìm điểm cực trị của một hàm số. Điểm cực trị bao gồm điểm cực đại (điểm lớn nhất) và điểm cực tiểu (điểm nhỏ nhất) của hàm số. Điểm cực trị thường đại diện cho các giá trị tối ưu trong các bài toán tối ưu hóa. Nhờ đạo hàm, chúng ta có thể xác định các điểm cực trị và sử dụng chúng để tối ưu hóa các hàm số trong nhiều lĩnh vực khác nhau như tài chính, kỹ thuật, và khoa học dữ liệu.
– Phân tích biên độ: Đạo hàm được sử dụng để phân tích biên độ của một hàm số. Biên độ cho biết sự tăng hoặc giảm của hàm số tại các điểm cụ thể. Đạo hàm có thể giúp xác định các điểm tăng/giảm đột ngột, các điểm uốn cong và các điểm tối đa/tối thiểu của biên độ. Ví dụ, trong kinh tế, đạo hàm được sử dụng để xác định lợi nhuận tối đa hoặc chi phí tối thiểu trong một công ty. Trong công nghệ thông tin, đạo hàm có thể được sử dụng để phân tích dữ liệu và tối ưu hóa hiệu suất của các thuật toán.
– Tính xấp xỉ: Đạo hàm được sử dụng để tính xấp xỉ giá trị của một hàm số tại một điểm cụ thể. Bằng cách tính toán đạo hàm tại một điểm, ta có thể xác định độ dốc của hàm số tại điểm đó và từ đó xấp xỉ giá trị của hàm số. Việc tính toán xấp xỉ giúp ta có cái nhìn tổng quan về hình dạng và biểu đồ của hàm số. Trong lĩnh vực khoa học dữ liệu, đạo hàm được sử dụng để xây dựng các mô hình dự đoán và xấp xỉ giá trị của các biến quan trọng.
– Giải phương trình: Đạo hàm cũng được sử dụng để giải phương trình. Bằng cách tìm các điểm mà đạo hàm của hàm số bằng không, ta có thể xác định các điểm mà hàm số cắt trục hoành và giải phương trình tương ứng. Điều này rất hữu ích trong việc tìm nghiệm của các phương trình đại số hoặc phương trình vi phân. Ví dụ, trong vật lý, đạo hàm được sử dụng để giải các phương trình chuyển động của các vật thể. Trong lĩnh vực kỹ thuật, đạo hàm có thể được sử dụng để giải các phương trình điều khiển và tối ưu hóa hiệu suất của các hệ thống.
– Phân tích đồ thị: Đạo hàm cung cấp thông tin quan trọng về đồ thị của hàm số. Bằng cách xác định các điểm cực trị, điểm uốn cong và các điểm tăng/giảm đột ngột, ta có thể hiểu rõ hơn về hình dạng và đặc điểm của đồ thị. Điều này giúp ta phân tích và diễn giải dữ liệu một cách chính xác và hiệu quả. Ví dụ, trong thống kê, đạo hàm được sử dụng để phân tích mô hình và tìm ra các điểm quan trọng trong dữ liệu. Trong lĩnh vực truyền thông và đồ họa, đạo hàm có thể được sử dụng để phân tích và tạo ra các hiệu ứng đồ họa phức tạp.
Đây chỉ là một số ứng dụng cơ bản của đạo hàm. Trên thực tế, đạo hàm còn có rất nhiều ứng dụng trong các lĩnh vực khác nhau như kỹ thuật, kinh tế, vật lý, thống kê, truyền thông, đồ họa và nhiều lĩnh vực khác.
4. Bài tập vận dụng liên quan:
Bài 1: Đạo hàm cấp hai của hàm số y = cos2x bằng biểu thức nào sau đây?
A. -2sin2x
B. -4cos2x
C. -4sin2x
D. 4cos2x
Đáp án: C
Bài 2: Đạo hàm của hàm số f(t) = a3t4 – 2at2 + 3t – 5a bằng biểu thức nào sau đây?
A. 4a3t3 – 4at + 3
B. 3a2t4 – 2t2 – 5
C. 12a2t3 – 4at – 2
D. 4a3t3 – 4at – 5
Đáp án: B
Bài 3: Cho hàm số f(x) = x2 + 2x, có Δx là số gia của đối số tại x = 1, Δy là số gia tương ứng của hàm số. Khi đó Δy bằng:
A. (Δx)2 + 2Δx
B. (Δx)2 + 4Δx
C. (Δx)2 + 2Δx – 3
D. 3
Đáp án: B
Bài 4: Cho hàm số ![]()
Đạo hàm của hàm số đã cho tại x = 1 là:
A. 1/4
B. -1/2
C. 0
D. 1/2
Đáp án: A
Bài 5: Cho hàm số f(x) = |x+1|. Khẳng định nào sau đây là sai?
A. f(x) liên tục tại x = -1
B. f(x) có đạo hàm tại x = -1
C. f(-1) = 0
D. f(x) đạt giá trị nhỏ nhất tại x = -1
Đáp án: B
Bài 6: Số gia của hàm số f(x) = 2x2 – 1 tại x0 = 1 ứng với số gia Δx = 0,1 bằng:
A. 1
B. 1,42
C. 2,02
D. 0,42
Đáp án: B
Bài 7: Cho hàm số ![]()
Đạo hàm của hàm số đã cho tại x = 1?
A. 1
B. 0
C. 1/4
D. -1/4
Đáp án: C
Bài 8: Đạo hàm của các hàm số sau tại các điểm đã cho: f(x) = 2x3 + 1 tại x = 2?
A. 10
B. 24
C. 22
D. 42
Đáp án: B
Bài 9: Cho hàm số f(x) = sin4x + cos4x – 2sin2xcos2x. Giá trị của f ‘(π/24) bằng:
A. -1
B. 1
C. 1/2
D. -1/2
Đáp án: A
Bài 10: Đạo hàm của các hàm số sau tại các điểm đã cho: f(x) = √(x2 + 1) tại ?
A. 1/2
B. -1/√2
C. 0
D. 3
Đáp án: A
Bài 11: Đạo hàm của hàm số y = (2x4-3x2-5x)(x2-7x) bằng biểu thức nào dưới đây?
A. (8x3-6x-5)(2x-7)
B. (8x3-6x-5)(x2-7x)-(2x4-3x2-5x)(2x-7)
C. (8x3-6x-5)(x2-7x)+(2x4-3x2-5x)(2x-7)
D. (8x3-6x-5)+(2x-7)
Đáp án: C




