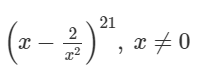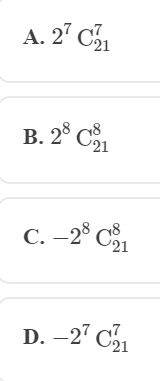Nhị thức Newton là một công thức quan trọng trong lĩnh vực toán học và vật lý. Được đặt theo tên của nhà toán học và nhà vật lý người Anh, Sir Isaac Newton, công thức này đã có ảnh hưởng sâu sắc trong nhiều lĩnh vực. Trong bài viết dưới đây hãy cùng chúng tôi tìm hiểu và làm những bài tập vận dụng liên quan đến công thức này nhé.
Mục lục bài viết
1. Tìm số hạng không chứa x trong khai triển nhị thức Newton:
Tìm số hạng không chứa x trong khai triển nhị thức Newton
Đáp án: D.
2. Nhị thức Newton là gì?
Nhị thức Newton là một công thức quan trọng trong lĩnh vực toán học và vật lý. Được đặt theo tên của nhà toán học và nhà vật lý người Anh, Sir Isaac Newton, công thức này đã có ảnh hưởng sâu sắc trong nhiều lĩnh vực.
Công thức này không chỉ được sử dụng để tính toán đạo hàm của một hàm số, mà còn có thể áp dụng trong nhiều bài toán khác nhau. Nhị thức Newton cho phép chúng ta tính toán đạo hàm của một hàm số bằng cách sử dụng các hệ số của chuỗi Taylor của hàm số đó. Nhờ công thức này, chúng ta có thể nhanh chóng xác định độ dốc của một đường cong tại một điểm cụ thể.
Việc hiểu và áp dụng nhị thức Newton sẽ giúp chúng ta nắm bắt được nhiều khía cạnh khác nhau của toán học và vật lý. Từ đó, chúng ta có thể áp dụng nó vào việc giải quyết các bài toán phức tạp và tạo ra những phát kiến mới trong lĩnh vực này.
Với sự quan trọng và ứng dụng đa dạng của nhị thức Newton, việc nắm vững công thức này là một yêu cầu cần thiết đối với những người học và nghiên cứu trong các lĩnh vực liên quan. Hãy tiếp tục khám phá và tìm hiểu thêm về nhị thức Newton để mở rộng kiến thức và khả năng trong lĩnh vực này.
3. Công thức nhị thức Newton:
Công thức nhị thức Newton được biểu diễn như sau:
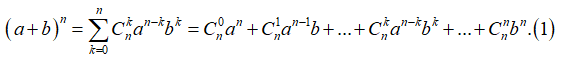
Lưu ý:
Trong biểu thức ở vế phải của công thức (1), chúng ta cần lưu ý những điểm sau đây để hiểu rõ hơn về cấu trúc và tính chất của biểu thức này:
– Đầu tiên, số lượng các hạng tử trong biểu thức là n + 1. Điều này có nghĩa là ta có tổng cộng n + 1 hạng tử được sắp xếp theo thứ tự từ cao đến thấp.
– Thứ hai, các hạng mũ của a trong mỗi hạng tử được sắp xếp theo thứ tự giảm dần từ n đến 0. Từ đó, ta có thể thấy rằng mỗi hạng mũ của a giảm dần đi 1 đơn vị khi ta di chuyển từ hạng tử trước đó sang hạng tử kế tiếp.
– Thứ ba, số mũ của b trong mỗi hạng tử được sắp xếp theo thứ tự tăng dần từ 0 đến n. Điều này có nghĩa là mỗi hạng mũ của b tăng dần đi 1 đơn vị khi ta di chuyển từ hạng tử trước đó sang hạng tử kế tiếp.
– Quan trọng nhất là tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n. Điều này đảm bảo rằng mỗi hạng tử trong biểu thức đóng góp đúng phần của n trong tổng quát.
– Cuối cùng, các hệ số của mỗi hạng tử được chia đều, tức là hệ số của hai hạng tử đầu và cuối cùng trong biểu thức là như nhau. Điều này mang lại tính cân đối và đẹp mắt cho biểu thức.
Nhìn chung, thông qua những quy tắc và tính chất trên, chúng ta có thể hiểu rõ hơn về cách xây dựng và phân tích biểu thức trong công thức (1).
4. Ứng dụng của nhị thức Newton:
Nhị thức Newton là một phương pháp tính toán hiệu quả và linh hoạt, có rất nhiều ứng dụng trong nhiều lĩnh vực khác nhau trong khoa học, công nghệ.
Trong lĩnh vực toán học, nhị thức Newton được sử dụng để giải quyết phương trình và hệ phương trình phi tuyến. Với phương pháp này, chúng ta có thể tìm ra các nghiệm xấp xỉ của các phương trình phi tuyến một cách nhanh chóng và chính xác. Điều này rất hữu ích trong việc giải quyết các bài toán phức tạp và đa dạng trong các lĩnh vực như kỹ thuật, kinh tế, và khoa học tự nhiên.
Một ứng dụng quan trọng khác của nhị thức Newton là tìm điểm cực trị của hàm số. Điểm cực trị là điểm cực đại hoặc cực tiểu của hàm số, và việc tìm ra các điểm này giúp chúng ta hiểu rõ hơn về đặc tính và biểu đồ của hàm số. Việc xác định các điểm cực trị có thể giúp chúng ta tối ưu hóa các quyết định và tìm ra các giá trị cực đại hoặc cực tiểu trong các bài toán tối ưu.
Nhị thức Newton cũng được sử dụng để xấp xỉ giá trị của hàm số tại một điểm cụ thể. Phương pháp này cho phép chúng ta tính toán giá trị xấp xỉ của hàm số, đồng thời cung cấp thông tin về sự biến đổi của hàm số trong một khoảng xác định. Điều này rất hữu ích trong việc nghiên cứu và mô phỏng các hệ thống phi tuyến, và cũng có thể được áp dụng trong việc tìm hiểu về các quá trình biến đổi trong các lĩnh vực như tài chính, kinh tế, và sinh học.
Trong lĩnh vực vật lý, nhị thức Newton được sử dụng để tính toán tốc độ và gia tốc trong các vấn đề vật lý. Với sự ứng dụng của phương pháp này, chúng ta có thể tính toán được các thông số vật lý quan trọng như tốc độ di chuyển và gia tốc của các vật thể, từ đó giúp chúng ta hiểu rõ hơn về chuyển động và tương tác giữa các vật thể trong không gian. Đây là một công cụ quan trọng trong việc nghiên cứu và phân tích các hiện tượng vật lý, từ chuyển động của vật thể nhỏ đến quỹ đạo của các hành tinh và sao.
Cuối cùng, nhị thức Newton cũng được sử dụng để tìm đường cong tiếp tuyến và đường cong song song với đường cong đã biết. Điều này giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các đường cong và tìm ra các đường cong tương đồng. Ứng dụng của phương pháp này rất đa dạng, từ việc xác định đường cong tiếp tuyến của một đường cong trong đồ họa máy tính, cho đến tìm ra các đường cong song song với các đường cong tự nhiên trong thiết kế và xây dựng.
Bên cạnh những ứng dụng truyền thống, nhị thức Newton còn có thể được áp dụng trong nhiều lĩnh vực mới và đa dạng. Ví dụ, trong lĩnh vực trí tuệ nhân tạo, nhị thức Newton được sử dụng để tối ưu hóa các mô hình học máy và xử lý dữ liệu lớn. Trong lĩnh vực y học, phương pháp này có thể được áp dụng để phân tích và dự đoán các biểu hiện bệnh lý. Nhị thức Newton cũng có thể được sử dụng trong lĩnh vực tài chính để xác định các mô hình và xử lý dữ liệu thống kê.
Như vậy, nhị thức Newton là một phương pháp mạnh mẽ và linh hoạt, có rất nhiều ứng dụng trong nhiều lĩnh vực khác nhau của khoa học và công nghệ. Từ việc giải quyết phương trình và hệ phương trình phi tuyến, tìm điểm cực trị, xấp xỉ giá trị của hàm số, tính toán tốc độ và gia tốc, đến tìm đường cong tiếp tuyến và song song, nhị thức Newton mang lại những giải pháp đáng tin cậy và hiệu quả cho rất nhiều bài toán trong thực tế.
Ngoài ra, nhị thức Newton còn đang được nghiên cứu và phát triển để áp dụng trong các lĩnh vực mới như trí tuệ nhân tạo, mô phỏng và dự đoán, và quản lý dữ liệu lớn. Với sự tiến bộ trong công nghệ và tính toán, nhị thức Newton ngày càng được cải thiện và tối ưu hóa để đáp ứng nhu cầu ngày càng cao của các ứng dụng thực tế.
4. Câu hỏi vận dụng liên quan:
Câu 1. Hệ số x6 trong khai triển (1 – 2x)10 thành đa thức là:
A. – 13440
B. – 210
C. 210
D. 13440
Đáp án: D
Câu 2. Số hạng không chứa x trong khai triển nhị thức Niu tơn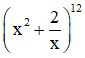
(x ≠ 0) là
Đáp án: D
Câu 3. Tìm số hạng không chứa x trong khai triển nhị thức Niu tơn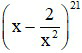 
, 
Đáp án: D
Câu 4. Tìm hệ số của số hạng chứa x6 trong khai triển x3(1 – x)8
A. – 28
B. 70
C. – 56
D. 56
Đáp án: C
Câu 5. Trong khai triển biểu thức (x + y)21 , hệ số của số hạng chứa x13y8 là:
A. 116280
B. 293930
C. 203490
D. 1287
Đáp án: C
Câu 6. Hệ số của x6 trong khai triển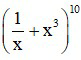 
bằng:
A. 792
B. 210
C. 165
D. 252
Đáp án: B
Câu 7. Trong khai triển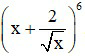 
, hệ số của x3, (x > 0) là:
A. 60
B. 80
C. 160.
D. 240
Đáp án: A
Câu 8. Tìm hệ số của x5 trong khai triển P(x) = (x + 1)6 + (x + 1)7 + … + (x + 1)12
A. 1715.
B. 1711.
C. 1287.
D. 1716.
Đáp án: A
Câu 9. Tìm số hạng không chứa x trong khai triển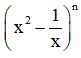 
biết
A. – 3003
B. – 5005
C. 5005
D. 3003
Đáp án: D
Câu 10. Tính tổng 
A. S = 210
B. S = 410
C. S = 310
D. S = 311
Đáp án: C
Câu 11. Tổng 
bằng
A. 42021
B. 22021 + 1
C. 42021 – 1
D. 22021 – 1
Đáp án: D
Câu 12. Số tập con của tập hợp gồm 2022 phần tử là
A. 2022
B. 22022
C. 20222
D. 2.2022
Đáp án: B
Câu 13. Trong khai triển (x – 2)100 = a0 + a1x1 + … + a100x100. Tổng hệ số: a0 + a1+ … + a100 là
A. – 1
B. 1
C. 3100
D. 2100
Đáp án: B
Câu 14. Tổng 
Bằng:
A. 2n-2
B. 2n-1
C. 22n-2
D. 22n-1
Đáp án: D
