Tìm m để (d) cắt (P) tại 2 điểm phân biệt thỏa mãn điều kiện

1. Các dạng bài tập tìm m để (d) cắt (P) tại hai điểm phân biệt thường gặp

1.1. Điều kiện để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt:

– Đường thẳng (d): y = mx + n và parabol (P): y = ax² (a khác 0) có phương trình hoành độ giao điểm là: ax² = mx + n ⇔ ax² – mx – n = 0(1)

– Để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt hay ∆ > 0

1.2. Các dạng toán thường gặp:

– Đường thẳng (d) cắt (P) tại hai điểm phân biệt nằm về bên trái trục tung khi và chỉ khi phương trình (1) có hai nghiệm âm phân biệt

– Đường thẳng (d) cắt (P) tại hai điểm phân biệt nằm về bên phải trục tung khi và chỉ khi phương trình (1) có hai nghiệm dương phân biệt

– Đường thẳng (d) cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm phân biệt trái dấu

– Đường thẳng (d) cắt (P) tại hai điểm có tọa độ thỏa mãn biểu thức cho trước (ta sẽ biến đổi biểu thức để sử dụng hệ thức Vi-ét của phương trình (1))

1.3. Phương pháp giải dạng toán này:

Cho đồ thị hàm số (P): y = ax²  (Điều kiện a khác 0) và đường thẳng y = mx + n

Bước 1: Viết phương trình hoành độ giao điểm của đồ thị hàm số parabol và đường thẳng, ta được : ax² = mx + n  <=> ax² – mx – n = 0 (*)

Bước 2: Xét điều kiện để đồ thị hàm số parabol có điểm chung với đường thẳng:

– Trường hợp 1:  Đồ thị hàm số parabol tiếp xúc với đường thẳng ( có 1 điểm chung) => phương trình hoành độ giao điểm có nghiệm kép ( Khi đó, Delta = 0 hoặc Delta phẩy = 0)

– Trường hợp 2: Đồ thị hàm số parabol cắt đường thẳng tại hai điểm phân biết ( có 2 điểm chung phân biệt ) => phương trình hoành độ giao điểm có hai nghiệm phân biệt ( khi đó 1 hoặc )

Bước 3: Xét điều kiện về vị trí giao điểm:

– Đường thẳng (d) cắt đồ thị hàm số parabol (P) tại hai điểm nằm phía trên trục hoành => thì a > 0

– Đường thẳng (d) cắt đồ thị hàm số parabol (P) tại hai điểm năm fphias dưới trục hoành => a< o

– Đường thẳng (d) cắt đồ thị hàm số parabol (P) tại hai điểm nằm cúng phía so với trục tung <=> phương trình hoành độ giao điểm có nghiệm cùng dấu <=>      hay  a. n < 0

– Đường thẳng (d) cắt đồ thị hàm số parabol (P) tại hai điểm cùng nằm bên phải trục tung <=> phương trình hoành độ giao điểm có nghiệm dương <=> và

– Đường thẳng (d) cắt đồ thị hàm số parabol (P) tại hai điểm cùng nằm phía bên trái trục tung thì phương trình hoành độ giao điểm có nghiệm âm khi và chỉ khi   và

– Đường thẳng (d) cắt đồ thị hàm số parabol (P) tại hai điểm nằm về hai phía trục tung<=> phương trình hoành độ giao điểm có hai nghiệm trái dấu với nhau <=>  hay a . n > 0

– Đường thẳng (d) cắt đồ thị hàm số parabol (P) tại hai điểm thoả mãn điều kiện khác: Sử dụng hệ thức Vi – ét, kết hợp biến đổi biểu thức.

Bước 4: Kết luận

2. Bài tập ví dụ về sự tương giao giữa parabol và đường thẳng:

Bài 1: Cho parabol (P): y = – 2x² và đường thẳng (d): y = 3x + m – 1. Tìm m để (d) cắt (P) tại 2 điểm nằm bên trái trục tung.

Hướng dẫn:

Đường thẳng (d) cắt parabol (P) tại hai điểm nằm bên trái trục tung ⇒ Hai điểm có hoành độ mang dấu âm.

Lời giải:

Phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d) là:

-2x² = 3x + m – 1 ⇔ 2x² + 3x + m – 1 = 0(1)

Có ∆ = b² – 4ac = 9 – 4.2.(m – 1) = 9 – 8m + 8 = 17 – 8m

Để (d) cắt (P) tại hai điểm nằm về bên trái trục tung khi và chỉ khi phương trình (1) có hai nghiệm âm phân biệt

Để phương trình (1) có hai nghiệm phân biệt ⇔ ∆ > 0 ⇔ 17 – 8m > 0 ⇔

Với , phương trình (1) có hai nghiệm phân biệt thỏa mãn Vi-ét

Để phương trình có hai nghiệm phân biệt âm

kết hợp với điều kiện

Vậy với  thì đường thẳng (d) cắt parabol (P) tại hai điểm nằm về bên trái của trục tung

Bài 2: Cho parabol (P): y = x² và đường thẳng (d) có phương trình y = 2x – m² + 9. Tìm m để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung.

Hướng dẫn:

Đường thẳng (d) cắt parabol (P) tại hai điểm nằm về hai phía của trục tung ⇒ Hai điểm có hoành độ trái dấu.

Lời giải:

Phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d) là:

x² = 2x – m² + 9 ⇔ x² – 2x + m² – 9 = 0 (1)

Để (d) cắt (P) tại hai điểm nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm trái dấu

⇔ m² – 9 < 0 ⇔ (m – 3)(m + 3) < 0

Vậy với -3 < m < 3 thì đường thẳng (d) cắt parabol (P) tại hai điểm nằm về hai phía của trục tung

Bài 3: Cho đường thẳng (d): y = x + m và parabol (P): y = x²

a, Tìm m để (d) cắt (P) tại hai điểm phân biệt nằm về cùng một phía với trục tung. Khi đó hai giao điểm nằm bên phải hay bên trái trục tung?

b, Tìm m để (d) cắt (P) tại 2 điểm phân biệt A và B sao cho khoảng cách giữa 2 hoành độ của điểm A và B bằng

Lời giải:

a, Phương trình hoành độ giao điểm của đường thẳng (d) và parabol (P) là:

x² = x + m ⇔ x² – x – m = 0(1)

Có ∆ = b² – 4ac

Để (d) cắt (P) tại hai điểm phân biệt x1, x2 khi và chỉ khi phương trình (1) có hai nghiệm phân biệt  ⇔ ∆ > 0 ⇔ 1 + 4m > 0 ⇔

Với  thì phương trình (1) có hai nghiệm phân biệt thỏa mãn hệ thức Vi-ét

Để (d) cắt (P) tại hai điểm phân biệt nằm về cùng một phía với trục tung khi và chỉ khi phương trình (1) có hai nghiệm cùng dấu ⇔ P > 0 ⇔ – m > 0 ⇔ m < 0 kết hợp với điều kiện  

Có S = 1 > 0 nên hai nghiệm của phương trình (1) là hai nghiệm cùng dấu dương

Vậy với  thì đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt cùng nằm về bên phải trục tung

b, Với  thì đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A(x₁; y₁) và B(x₂; y₂) thỏa mãn Vi-ét:

Khoảng cách giữa hai điểm bằng

Vậy với =53/3 thì đường thẳng (d) cắt parabol (P) tại hai điểm A và B mà khoảng cách giữa chúng bằng

Bài 4: Cho parabol (P): và đường thẳng (d): y = mx – 1. Tìm m để (d) cắt (P) tại hai điểm có hoành độ x1, x2 thỏa mãn

Lời giải:

Phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d):

(1)

Để (d) cắt (P) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt

Có ∆ = b’² – ac = m² + 2 > 0 với mọi m

Vậy với mọi m thì phương trình (1) có hai nghiệm phân biệt thỏa mãn hệ thức Vi-ét:

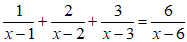
3. Bài tập tự luyện về tìm m để (d) cắt (P) tại 2 điểm phân biệt thỏa mãn điều kiện:

Bài 1: Cho đường thẳng (d): y = mx + 1 và parabol (P): . Tim m để (d) cắt (P) tại hai điểm phân biệt A và B sao cho tam giác OAB có diện tích bằng 3/2.

Lời giải:

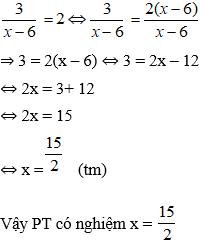
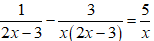
Vậy với m=+_1/2 thì đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B sao cho tam giác OAB có diện tích bằng 3/2

Bài 2: Cho đồ thị (C):y = (mx – 1)/(x + 2) và đường thẳng d: y = 2x – 1. Xác định giá trị của tham số m để (C) cắt d tại hai điểm phân biệt A, B sao cho AB=√10

Lời giải:

Phương trình hoành độ giao điểm (mx – 1)/(x + 2) = 2x – 1 (1)

Điều kiện x ≠ -2

Khi đó (1) ⇔ mx – 1 = (2x – 1)(x + 2)

⇔ 2x² – (m – 3)x – 1 = 0 (2)

(d) cắt (C_m) tại hai điểm phân biệt A, B ⇔ (1) có hai nghiệm phân biệt

⇔ (2) có hai nghiệm phân biệt khác -2

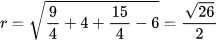
Khi đó AB = √((x₁ – x₂)² + 4(x₁ – x₂)² ) = √10 ⇔ 5[(x₁ + x₂ )² – 4x₁ x₂ ] = 10

⇔ ((m – 3)/2)² + 2 = 2

⇔ m = 3 (thỏa mãn)

Vậy giá trị cần tìm là m = 3

Bài 3: Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x^2 và đường thẳng (d): y = 2x + m (m là tham số). Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm A, B nằm về hai phía của trục tung, sao cho diện tích có diện tích gấp hai lần diện tích (M là giao điểm của đường thẳng d với trục tung).

Lời giải:

(d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi

Khi đó 2 nghiệm của phương trình là:

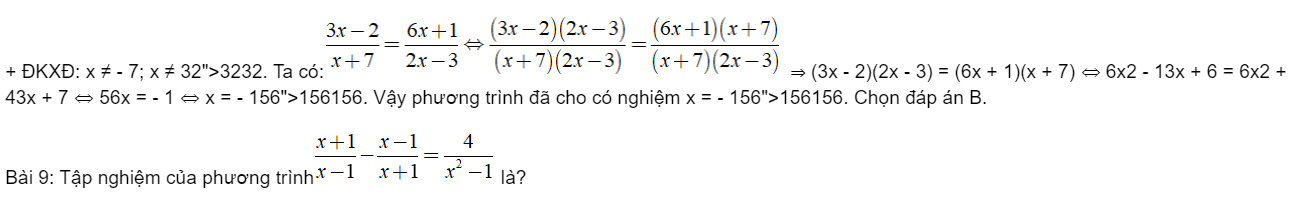
Kẻ BB’ ⊥ OM ; AA’ ⊥ OM

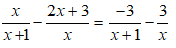
Ta có:

$S_{AOM}$ = 1/2 AA’.OM ; $S_{BOM}$ = 1/2 BB’.OM

Theo bài ra:

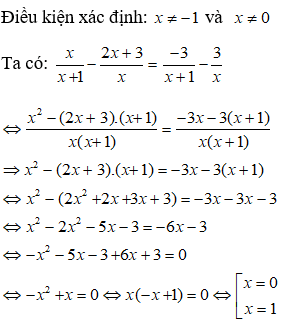
Do m > 0 nên m = 8

Vậy với m = 8 thì thỏa mãn điều kiện đề bài