Tập xác định của một hàm số là khái niệm cơ bản trong toán học, đó là phạm vi các giá trị mà biến độc lập có thể nhận để hàm số đó có ý nghĩa và giá trị xác định. Việc xác định tập xác định là bước đầu tiên và quan trọng nhất để hiểu rõ tính chất và ứng dụng của một hàm số. Vậy tập xác định của hàm số y = cotx là gì?
Mục lục bài viết
1. Tập xác định của hàm số y = cot 2x là:
A. .svg){kind=small}
B. .svg){kind=small}
C. .svg){kind=small}
D. .svg){kind=small}
Đáp án:
Điều kiện xác định của hàm số y = cot 2x là:
sin 2x ≠ 0
=> 2x ≠ kπ
=> .svg){kind=small}
Chọn đáp án D
2. Tập xác định của hàm số là gì?
Tập xác định của một hàm số là khái niệm cơ bản trong toán học, đó là phạm vi các giá trị mà biến độc lập có thể nhận để hàm số đó có ý nghĩa và giá trị xác định. Trong mọi ứng dụng của toán học và khoa học, việc xác định tập xác định là bước đầu tiên và quan trọng nhất để hiểu rõ tính chất và ứng dụng của một hàm số.
Để xác định tập xác định của một hàm số, ta thường phải xem xét các hạn chế và ràng buộc có thể xuất hiện trong biểu thức của nó. Trong quá trình này, chúng ta cần chú ý đến các tình huống như phép chia cho 0, căn bậc hai của số âm, hoặc các điều kiện khác có thể làm cho hàm số trở nên vô lý hoặc không xác định.
Ngoài ra, một số hàm số có thể có các ràng buộc khác, như miền xác định của hàm số căn bậc hai chỉ bao gồm các số không âm. Điều này bởi vì chúng ta không thể lấy căn bậc hai của một số âm trong miền thực.
Tóm lại, tập xác định của một hàm số là một phần không thể thiếu để đảm bảo rằng hàm số đó có ý nghĩa và có thể được sử dụng một cách hợp lý trong các phép toán và tính toán. Đây là bước quan trọng đầu tiên để hiểu và ứng dụng hàm số trong nhiều lĩnh vực khác nhau của toán học và khoa học.
3. Các tìm tập xác định của hàm số:
Để tìm tập xác định của một hàm số, trước tiên chúng ta cần hiểu rõ biểu thức của hàm số đó và các hạn chế về giá trị của biến độc lập mà hàm số có thể chấp nhận. Dưới đây là quy trình chi tiết để xác định tập xác định của một hàm số:
– Xác định biểu thức của hàm số: Trước hết, chúng ta cần biết biểu thức của hàm số, nghĩa là cách mà hàm số được biểu diễn dưới dạng toán học.
– Loại trừ các giá trị không xác định: Tiếp theo, chúng ta cần loại bỏ các giá trị của biến độc lập mà có thể dẫn đến việc hàm số không xác định hoặc không tồn tại. Cụ thể, các trường hợp này thường bao gồm việc chia cho 0 hoặc sử dụng căn bậc hai của một số âm trong biểu thức của hàm số.
– Tạo ra tập hợp của các giá trị hợp lệ: Sau khi loại bỏ các giá trị không xác định, chúng ta sẽ thu được một tập hợp các giá trị biến độc lập mà khi sử dụng trong hàm số, hàm số sẽ có giá trị xác định.
– Xác định tập xác định của hàm số: Tập xác định của hàm số sẽ là tập hợp của các giá trị biến độc lập mà khi được sử dụng trong hàm số, hàm số sẽ có giá trị xác định và có ý nghĩa trong ngữ cảnh của bài toán cụ thể.
4. Những ứng dụng của tập xác định của hàm số:
Tập xác định của hàm số là tập hợp các giá trị của biến độc lập mà hàm số được định nghĩa và tồn tại. Khái niệm này đóng vai trò quan trọng trong toán học và có nhiều ứng dụng thực tế.
– Xác định tính chất của hàm số: Tập xác định giúp chúng ta hiểu rõ tính chất của hàm số như tính liên tục, tính chẵn lẻ, tính tăng giảm, và tính toàn phần. Bằng cách xác định tập xác định, chúng ta biết được những giá trị nào mà biến độc lập có thể nhận mà hàm số vẫn giữ nguyên tính chất của mình.
– Xác định miền giá trị của hàm số: Tập xác định cũng liên quan chặt chẽ đến miền giá trị của hàm số. Miền giá trị là tập hợp các giá trị mà hàm số có thể nhận. Bằng cách xác định tập xác định, ta có thể suy ra được miền giá trị của hàm số, tức là tập hợp các giá trị mà hàm số có thể đạt được.
– Ứng dụng trong giải bài toán thực tế: Trong thực tế, việc xác định tập xác định của hàm số thường được sử dụng để giải quyết các bài toán thực tế. Ví dụ, trong kinh doanh và tài chính, tập xác định có thể đại diện cho các điều kiện hoặc hạn chế trong một bài toán.
– Tính toán và phân tích hàm số: Tập xác định cũng giúp ta tính toán và phân tích hàm số một cách hiệu quả. Việc hiểu rõ tập xác định giúp ta chọn lựa các phương pháp phân tích phù hợp để hiểu rõ bản chất của hàm số.
– Ứng dụng trong khoa học và kỹ thuật: Trong nhiều lĩnh vực khoa học và kỹ thuật, như vật lý, hóa học, máy tính học, và kỹ thuật điện, tập xác định của hàm số được sử dụng để mô hình hóa và dự đoán các hiện tượng và quá trình.
Tóm lại, tập xác định của hàm số đóng vai trò quan trọng trong nhiều lĩnh vực của toán học và có nhiều ứng dụng thực tế. Việc hiểu rõ và áp dụng khái niệm này giúp ta giải quyết các bài toán phức tạp và phân tích hàm số một cách chính xác và hiệu quả.
5. Bài tập trắc nghiệm vận dụng liên quan:
Bài 1: Tập xác định D của hàm số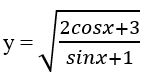 
là
A. D = R\ {-π/2+kπ, k ∈ Z}
B. D = R\ {-π/2+k2π, k ∈ Z}
C. D = R
D. D = R\ {π/2+k2π, k ∈ Z}
Đáp án: B
Bài 2: Tìm tập xác định của hàm số sau: y = 2017/sinx
A. D = R
B. D = R\ {kπ, k ∈ Z}
C. D = R\{0}
D. D = R\ {π/2+kπ, k ∈ Z}
Đáp án: B
Bài 3: Tìm tập giá trị của hàm số sau: 
A. D = R
B. D = R\ {-π/2+k2π, k ∈ Z}
C. D = R\{0}
D. D = R\ {π/2+k2π, k ∈ Z}
Đáp án: A
Bài 4: Tìm tập xác định của hàm số sau 
A. D = [0,2π]
B. D = ∅
C. D = R
D. D = [-2,+∞]
Đáp án: C
Bài 5: Hàm số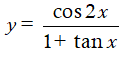 
không xác định trong tập nào sau đây?
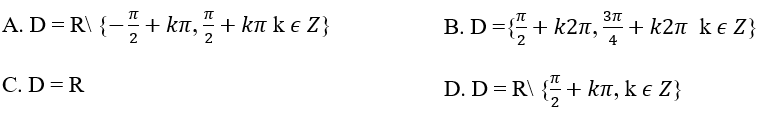
Đáp án: B
Bài 6: Hàm số y = 1/sinx không xác định trong tập nào sau đây?
A. D ={-π/2+kπ, k ∈ Z}
B. D = {-π/2+k2π, k ∈ Z}
C. D = R
D. D = {π+k2π, k ∈ Z}
Đáp án: D
Bài 7: Hàm số y = tanx xác định trong tập nào sau đây?
A. D = {-π/2+kπ, k ∈ Z}
B. D = {-π/2+k2π, k ∈ Z}
C. D = R
D. D = {π+k2π, k ∈ Z}
Đáp án: A
Bài 8: Tìm tập giá trị của hàm số sau: 
A. D = [0,+∞)
B. D = ∅
C. D = R
D. D = [1,√3]
Đáp án: D
Bài 9: Tìm tập giá trị của hàm số sau: y = 2017/sinx
A. D = R\ {0}
B. D = [-2017,2017]
C. D = R
D. D = (-∞,-2017]∪[2017,+∞)
Đáp án: D
Bài 10: Tìm tập giá trị của hàm số sau: 
A. D = R\ {0}
B. D = [0,1]
C. D = R
D. D =[0,+∞)
Đáp án: B
Bài 11: Tìm tập xác định của hàm số sau 
A. D = R\ {-π/2+kπ, k ∈ Z}
B. D = R\ {-π/2+k2π, k ∈ Z}
C. D = R
D. D = R\ {π/2+k2π, k ∈ Z}
Đáp án: C
Bài 12: Tìm tập giá trị của hàm số sau 
A. D = [1,√3]
B. D = [0,1]
C. D = R
D. D = [0,√3]
Đáp án: A
Bài 13: Tìm tập xác định của hàm số sau: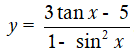 
A. D = R\ {-π/2+kπ, k ∈ Z}
B. D = (-∞,2]
C. D = R
D. D = R\ {π/2+k2π, k ∈ Z}
Đáp án: C
Bài 14: Tìm tập xác định D của hàm số y = (sinx + 2)/ (sinx.cos2x)
A. D = R\ {kπ/2, k ∈ Z}
B. D = R \ {π/2+kπ, k ∈ Z}
C. D = R\ {π/2+k2π, k ∈ Z}
D. D = R\ {kπ, k ∈ Z}
Đáp án: A
