Chắc hẳn số nguyên tố đã quá quen thuộc trong cuộc sống thường ngày cũng như trong quá trình học tập của các học sinh. Bởi số nguyên tố là kiến thức nền tảng quan trọng để cho học sinh học tốt môn toán. Vậy số nguyên tố gì, tính chất của số nguyên tố ra sao?
Mục lục bài viết
1. Số nguyên tố là gì?
Số nguyên tố là tập hợp các số tự nhiên lớn hơn 1, chia hết cho 1 và chính nó. Nói theo một cách đơn giản, số nguyên tố là những số chỉ có đúng hai ước số là 1 và chính nó.
Ví dụ: 2, 3, 5, 7, 11, 13, 17, 23, 29,…đều được gọi là số nguyên tố.
Chú ý:
Các số tự nhiên lớn hơn 1 không phải là số nguyên tố được gọi là hợp số. Ví dụ: số 7 là số nguyên tố vì cách duy nhất để viết nó dưới dạng một tích là: (1 x 7) hoặc (7 x 1), có một thừa số là chính số 7. Nhưng số 6 là hợp số vì nó là tích của hai số ( 2 × 3 ) mà cả hai số 2 và số 3 đều nhỏ hơn số 6.
Có hai trường hợp không được xét là số nguyên tố là số 0 và số 1.
Những khái niệm khác có liên quan:
Số nguyên tố cùng nhau là số tự nhiên có ước chung lớn nhất bằng một.
Ví dụ: Số 7 và số 8 có ước chung lớn nhất bằng 1 (7 = 1 x 7; 8 = 1 x 2 x 2 x 2). Như vậy, ta kết luận rằng số 7 và số 8 là hai số nguyên tố cùng nhau.
Số siêu nguyên tố là số nguyên tố mà khi ta bỏ một số tùy ý vào các chữ số bên phải của nó thì phần còn lại vẫn tạo thành một số nguyên tố.
Ví dụ: Số 1337 là số siêu nguyên tố có 4 chữ số vì nếu bỏ đi số 37 thì số 13 cũng là số nguyên tố, hay bỏ số 7 thì số 133 cũng vẫn là số nguyên tố. Ngoài ra, các số: 2333, 2339, 2393, 7333, 7393, 37337, … cũng được gọi là siêu nguyên tố.
Tích các thừa số nguyên tố là phép nhân giữa các số nguyên tố.
Ví dụ: 3 × 5 × 7 = 105. Trong đó số 3, 5, 7 là các số nguyên tố.
2. Tính chất của số nguyên tố:
Số nguyên tố mang những tính chất sau đây:
– Số 2 vừa là số nguyên tố nhỏ nhất và đồng thời vừa là số nguyên tố chẵn duy nhất;
– Không thể giới hạn số lượng số nguyên tố cũng như tập hợp các số nguyên tố, Bởi số nguyên tố là vô hạn;
– Tích của hai số nguyên tố không thể là một số chính phương khi hai số nguyên tố đó nhân với nhau;
– Ước tự nhiên nhỏ nhất khác 1 của một số tự nhiên được coi là số nguyên tố;
– Một tập hợp số a bất kỳ có ước nhỏ nhất là một số dương b với điều kiện b khác 1 và b phải nhỏ hơn căn bậc hai của a thì b là số nguyên tố.
3. Bảng số nguyên tố:
Bảng số nguyên tố:
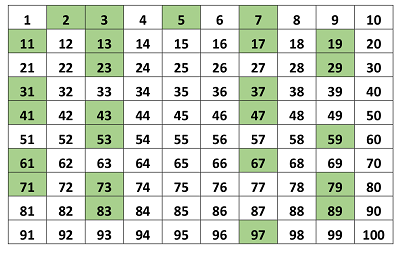
– Số 2 là số nguyên tố nhỏ nhất và có 1 chữ số.
– Số 11 là số nguyên tố nhỏ nhất và có 2 chữ số.
– Số 101 là số nguyên tố nhỏ nhất và có 3 chữ số.
– Số 97 là số nguyên tố lớn nhất và có 2 chữ số.
– Số 997 là số nguyên tố lớn nhất và có 3 chữ số.
4. Các dạng bài tập về số nguyên tố:
Dạng 1: Nhận biết số nguyên tố, chứng minh một số là số nguyên tố.
Dạng 2: Liên quan đến dấu hiệu nhận biết một số nguyên tố.
Dạng 3: Liên quan đến ước và bội của số nguyên tố.
Dạng 4: Liên quan đến tổng, hiệu của số nguyên tố.
Dạng 5: Bài toán về các số nguyên tố cùng nhau.
Dạng 6: Các bài toán về giải phương trình nghiệm nguyên nhờ tính chất nguyên tố.
Dạng 7: Tìm số nguyên tố thoả mãn điều kiện cho trước.
5. Cách tìm số nguyên tố:
Cách 1: Kiểm tra số nguyên tố.
Nếu số đó nhỏ hơn 2 thì ta kết luận rằng đó không phải số nguyên tố.
Nếu số đó không có ước nào trong đoạn từ 2 đến căn bậc hai của n thì nó là số nguyên tố. Còn nếu số đó có ước trong đoạn từ 2 đến căn bậc hai của thì đó không phải là số nguyên tố.
Cách 2: Chia thử nghiệm.
Chia n cho tất cả các số nguyên từ 2 đến căn bậc hai của n. Nếu số nguyên nào chia hết cho n thì n là hợp số, còn không có thì n là số nguyên tố. ( số phép chia sẽ tăng dần theo cấp số nhân khi số chữ số của số nguyên đó ngày càng nhiều.)
Cách 3: Thao tác lặp từng phần tử với bước nhảy 1.
Để kiểm tra số n có phải là số nguyên tố hay không, ta cần áp dụng các bước sau:
Bước 1: Nhập vào số n.
Bước 2: Nếu số n nhỏ hơn 2 thì n không phải là số nguyên tố.
Bước 3: Lặp từ 2 tới (n-1), nếu trong khoảng này tồn tại số mà n không chia hết thì kết luận rằng số n là số nguyên tố, ngược lại nếu trong khoảng này số n chia hết thì số n không phải là số nguyên tố.
Cách 4: Thao tác lặp từng phần tử với bước nhảy 2.
Vì số 2 là số nguyên tố chẵn duy nhất nên ta loại số 2 ra khỏi vòng lặp. Vì vậy trong thân vòng lặp chỉ cần kiểm tra các số lẻ.
6. Ví dụ minh hoạ về số nguyên tố:
Ví dụ 1: Cho một số nguyên tố bằng tổng của hai chữ số nguyên tố và bằng hiệu của hai số nguyên tố. Hãy tìm số nguyên tố đó.
Hướng dẫn giải:
Giả sử x, y, z, g, h là các số nguyên tố ( g lớn hơn h )
Theo giả thiết ta có: x = y + z = g – h => x > 2. Suy ra x là một số nguyên tố lẻ.
Ta có: y + z = g – h là số nguyên tố lẻ. Bởi vì y và g là các số nguyên tố nên suy ra y và g là số lẻ
Suy ra: z và h là số chẵn.
Ta có: z = h = 2 ( do z và h là các số nguyên tố )
Ta lại có: x = y + 2 = d – 2 nên suy ra g = y + 4. Như vậy ta cần phải tìm số nguyên tố y sao cho y + 2 và y + 4 cũng là số nguyên tố => y = 3
Kết luận: Vậy số nguyên tố cần tìm là bằng 5.
Ví dụ 2: Cho tổng và hiệu của hai số nguyên tố đều là số nguyên tố. Tìm hai số nguyên tố đó?
Hướng dẫn giải:
Giả sử a, b, c, d là các số nguyên tố. ( a lớn hơn b )
Theo bài ra ta có: a -b = c và a + b = d . Suy ra c + d = d – b
=> a > 2 và a là số nguyên tố lẻ. Suy ra c + b và d – b cũng là số lẻ.
Vì b, c và d đều là số nguyên tố nên để c + b và d – b là số lẻ thì b là số chẵn.
Vậy b = 2
Ta có: a – 2 và a + 2 cũng là số nguyên tố.
– Nếu a = 5 => a – 2 = 3 và a + 2 = 7 đều là số nguyên tố.
– Nếu a là một số khác 5. Ta xét 2 trường hợp sau:
Trường hợp 1: a chia 3 dư 1. Suy ra: a + 2 chia hết cho 3 không là số nguyên tố.
Trường hợp 2: a chia 3 dư 2. Suy ra: a – 2 chia hết cho 3 không là số nguyên tố.
Theo đó, chỉ có số nguyên tố 5 là số duy nhất thoả mãn số nguyên tố a.
Kết luận: hai số nguyên tố cần tìm là số 2 và số 5.
Ví dụ 3: Hãy tìm số nguyên tố nhỏ nhất trong ba chữ số sao cho tổng ba số nguyên tố đó bằng 1322?
Hướng dẫn giải:
Theo giả thiết thì tổng của ba số nguyên tố đó bằng 1322 là một số chẵn.
=> Trong ba số nguyên tố đó có thể là ba số chẵn hoặc là hai số lẻ và một số chẵn.
=> Do vậy, số nhỏ nhất trong ba số nguyên tố là số 2.
Ví dụ 4: Trong các nhận định dưới đây nhận định nào đúng, nhận định nào sai? Giải thích tại sao?
A. Số nguyên mà nhỏ hơn số 1 là số nguyên âm.
B. Tất cả số nguyên tố đều có số tận cùng là 3, 7, 9.
C. Số 2 là số nguyên tố chẵn duy nhất và là số nguyên tố nhỏ nhất.
D. Hai tia đối nhau là hai tia có chung gốc.
Hướng dẫn giải:
Lưu ý: – Số nguyên tố là những số chỉ có đúng hai ước số là 1 và chính nó.
– Số nguyên bao gồm số nguyên âm, số nguyên dương và số 0.
A. Nhận định này sai. Bởi vì số 0 là số nguyên nhỏ hơn 1. Số 0 không phải là số nguyên dương và cũng không phải là số nguyên âm.
B. Nhận định này sai. Bởi vì ngoài những số tận cùng là 3, 7, 9 là số nguyên tố ra thì có rất nhiều số tận cùng là số 3, 7, 9 nhưng lại hợp số. Ví dụ: số 39 có tận cùng là số 9 nhưng lại là hợp số; số 303 có tận cùng là số 3 nhưng lại là hợp số;…
C. Nhận định này đúng.
D. Nhận định này đúng.
Ví dụ 5: Hãy chứng minh rằng: Có vô số số nguyên tố có dạng 4x + 3 ( với x ∈ N)
Hướng dẫn giải:




