Phương pháp giải phương trình bậc hai một ẩn chi tiết

1. Phương pháp giải phương trình bậc hai một ẩn chi tiết:

Phương trình bậc hai một ẩn có dạng như sau ax² + bx + c = 0  (a ≠ 0). Để có thể giải giải phương trình bậc hai một ẩn, ta tiến hành làm như sau:

B₁: Xác định các hệ số a, b, c

B₂: Tính ∆ = b² – 4ac

+ Nếu ∆ < 0 thì phương trình vô nghiệm

+ Nếu ∆ = 0 thì phương trình có nghiệm kép:  

+ Nếu ∆ > 0 thì phương trình có 2 nghiệm phân biệt:

* Công thức nghiệm thu gọn: Dùng khi hệ số b = 2bꞌ

Phương trình ax² + bx + c = 0 (a ≠ 0) có ∆ꞌ = (bꞌ)² – ac (b = 2bꞌ)

+ Nếu ∆ꞌ < 0 thì phương trình vô nghiệm

+ Nếu ∆ꞌ = 0 thì phương trình có nghiệm kép:  

+ Nếu ∆ꞌ > 0 thì phương trình có 2 nghiệm phân biệt

* Nếu hệ số b = 0 thì phương trình có dạng: ax² + c = 0 (2)

Để giải phương trình (2) ngoài cách dùng  ∆ hoặc ∆ꞌ ở trên ta có thể làm như sau:

+ Nếu ac > 0 thì phương trình vô nghiệm

+ Nếu ac = 0 thì phương trình có nghiệm kép x = 0

+ Nếu ac < 0 thì phương trình có 2 nghiệm phân biệt

*Nếu hệ số c = 0 thì phương trình có dạng: ax² + bx = 0 (3)

Để giải phương trình (3) ngoài cách dùng  ∆ hoặc ∆ꞌ ở trên ta có thể làm như sau

Các bước tiến hành giải phương trình bậc hai một ẩn như sau:

Bước 1: Lập phương trình Gọi ẩn và đặt điều kiện tùy theo đề bài. Biểu diễn các đại lượng khác của bài toán theo ẩn vừa gọi. Dựa vào bài toán đề bài, lập phương trình theo dạng đã học. Bước 2: Tìm nghiệm của phương trình vừa lập. Bước 3: So sánh kết quả vừa tìm được và chọn nghiệm thích hợp.

2. Các ví dụ về phương trình bậc hai một ẩn:

Ví dụ 1: Giải phương trình x² + 3x + 3 = 0

Giải

Ta có: a = 1; b = 3; c = 3 ⇒ ∆ = b² – 4ac = 9 – 12 = – 3 < 0

Vậy phương trình vô nghiệm.

Ví dụ 2: Giải phương trình  x² + x – 5 = 0

Giải

Ta có: a = 1; b = 1; c = – 5 ⇒ ∆ = b² – 4ac = 1 + 20 = 21 > 0

Vậy phương trình có hai nghiệm phân biệt:

Ví dụ 3: Giải phương trình x² + 2x + 2 = 0

Giải

Ta có: a = 1; b = 2; c = 2

⇒ ∆ = b² – 4ac =

Vậy phương trình có nghiệm kép:

Ví dụ 4: Giải phương trình sau:

Giải

Ta có: a = 3; bꞌ = -√3 ; c = -3 ⇒ ∆ꞌ = (bꞌ)² – ac =

Vậy phương trình có hai nghiệm phân biệt:

Ví dụ 5: Giải các phương trình sau:

a. 2x² + 3 = 0

b. -7x² = 0

c. 3x² – 12 = 0

Giải

Vậy phương trình có 2 nghiệm phân biệt: x = 2, x = -2

Ví dụ 6: Giải các phương trình sau

a. 3x² +8x = 0

b. 5x² – 10x = 0

Giải

a. Ta có:

Vậy phương trình có 2 nghiệm là: x = 0,

b. Ta có:

Vậy phương trình có 2 nghiệm là: x = 0, x = 2

3. Bài tập vận dụng và lời giải:

Câu 1: Một nghiệm của phương trình 3x² + 5x – 2 = 0 là

A. -2

B. -1

C. -5

D. 0

Giải

Ta có: a = 3; b = 5; c = -2 ⇒ ∆ = b² – 4ac = 5² – 4.3.(-2) = 49 > 0

Phương trình có hai nghiệm phân biệt:

Vậy đáp án đúng là A

Câu 2: Số nghiệm của phương trình 3x² – 6x + 3 = 0 là

A. 3

B. 2

C. 1

D. 0

Giải

Ta có: a = 3; bꞌ = -3; c = 3 ⇒ ∆ꞌ = (bꞌ)² – ac = (-3)² – 3.3 = 9 – 9 = 0

Suy ra phương trình có một nghiệm

Vậy đáp án đúng là C

Câu 3: Giả sử x₁, x₂ (x₁ > x₂) là hai nghiệm của phương trình 5x² – 6x + 1 = 0.      Tính 2x₁ + 5x₂

A. 6

B. 5

C. 4

D. 3

Giải

Ta có: a = 5; bꞌ = -3; c = 1 ⇒ ∆ꞌ =(bꞌ)² – ac = (-3)² – 5.1 = 9 – 5 = 4 > 0

Suy ra phương trình có hai nghiệm phân biệt

Vậy đáp án đúng là D

Câu 4: Số thực nào sau đây là nghiệm của phương trình x² – x + 8 = 0

A. 2

B. 10

C. -15

D. Không có

Giải

Ta có: a = 1; b = -1; c = 8 ⇒ ∆ = b² – 4ac = (-1)² – 4.1.8 = -31 <  0

Vậy phương trình vô nghiệm

Vậy đáp án đúng là D

Câu 5: Giả sử x₁ < x₂ là hai nghiệm của phương trình x² -7x – 8 = 0. Tính 2x₁

A. -2

B. 1

C. -1

D. 6

Giải

Ta có: a = 1; b = -7; c = -8 ⇒  ∆ = b² – 4ac = (-7)² – 4.1.(-8) = 81 >  0

Phương trình có hai nghiệm phân biệt

Suy ra x₁ = -1 do đó 2x₁ = -2

Vậy đáp án đúng là A

Câu 6: Nghiệm của phương trình 3x² + 15 = 0 là

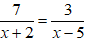
Giải

Phương trình 3x² + 15 = 0 ⇔ 3x² = -15 ⇔ x² = -5 (vô nghiệm)

Vậy đáp án đúng là D

Câu 7: Nghiệm của phương trình x² + 13x = 0 là

A. 13 và -13

B. 0 và -13

C. 0 và 13

D. Vô nghiệm

Giải

Phương trình x² + 13x = 0

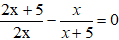
Vậy đáp án đúng là B

Câu 8: Cho phương trình  2x² + 4x + 1 = -x² – x – 1. Tính |x₁ – x₂|

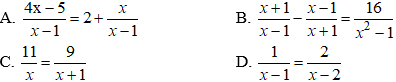
Giải

Phương trình 2x² + 4x + 1 = -x² – x – 1

Ta có: a = 3; b = 5; c = 2 ⇔ ∆ = b² – 4ac = (5)² – 4.3.2 = 1 >  0

⇒ Phương trình có hai nghiệm phân biệt

Vậy đáp án đúng là A

Câu 9: Cho phương trình x² – 10x + 21 = 0. Khẳng định nào sau đây đúng

A. Phương trình vô nghiệm

B. Phương trình có nghiệm không nguyên

C. Phương trình có 1 nghiệm

D. Phương trình có 2 nghiệm nguyên

Giải

Ta có: a = 1; b = -10; c = 21 ⇒ ∆ = b² – 4ac = (-10)² – 4.1.21 = 16 >  0

Phương trình có hai nghiệm phân biệt

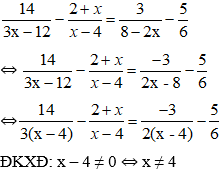
Vậy đáp án đúng là D

Câu 10: Số nghiệm của phương trình  4x² – 6x = -2x là

A. 1

B. 0

C. 2

D. 3

Giải

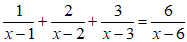
Đáp án đúng là đáp án C.

Câu 11: Giải các phương trình sau:

1. x²-3x+2=0
2. x²+x-6=0

Hướng dẫn:

1. Δ=(-3)²-4.2=1. Vậy

Ngoài ra, ta có thể áp dụng cách tính nhanh: để ý  suy ra phương trình có nghiệm là x₁=1 và x₂=2/1=2

1. Δ=1²-4.(-6)=25. Vậy

Câu 12: Giải phương trình:

1. x²-4=0
2. x²-3x=0

Hướng dẫn:

1. x²-4=0 ⇔ x²=4 ⇔ x=2 hoặc x=-2
2. x²-3x=0 ⇔ x(x-3)=0 ⇔ x=0 hoặc x=3

Câu 143: Giải các phương trình sau:

1. 4x⁴-3x²-1=0

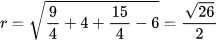
Hướng dẫn:

1. Đặt t=x² (t≥0), lúc này phương trình trở thành:

4t²-3t-1=0, suy ra t=1 hoặc t=-¼

• t=1 ⇔ x²=1  ⇔ x=1 hoặc x=-1.
• t=-¼ , loại do điều kiện t≥0

Vậy phương trình có nghiệm x=1 hoặc x=-1.

1. Ta có:

Câu 14: Giải và biện luận theo tham số m: mx²-5x-m-5=0 (*) Hướng dẫn: Xét m=0, khi đó (*) ⇔ -5x-5=0 ⇔ x=-1 Xét m≠0, khi đó (*) là phương trình bậc 2 theo ẩn x. – – Vì Δ≥0 nên phương trình luôn có nghiệm: + Δ=0  ⇔ m=-5/2, phương trình có nghiệm duy nhất. + Δ>0 ⇔ m≠-5/2, phương trình có 2 nghiệm phân biệt:

 Câu 15: Cho phương trình x2+mx+m+3=0 (*). Tìm m để phương trình (*) có 2 nghiệm thỏa mãn: Hướng dẫn: Để phương trình (*) có nghiệm thì:  Khi đó, gọi x₁ và x₂ là 2 nghiệm, theo định lý Viet:  

Mặt khác:

Theo đề:  Thử lại: – Khi m=5, Δ=-7 <0 (loại) – Khi m=-3, Δ=9 >0 (nhận) vậy m = -3 thỏa yêu cầu đề bài.

Câu 16: Thay x = -3 vào phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0, ta có: (m – 2).(-3)2 – (m2 + 1).(-3) + 3m = 0 <=> 9m – 18 + 3m2 + 3 + 3m = 0 <=> 3m2 + 12m – 15 = 0 <=> m2 + 4m – 5 = 0 <=> m2 – m + 5m – 5 = 0 <=> m. (m – 1) + 5.(m – 1) = 0 <=> (m – 1).(m + 5) = 0 <=> m = 1 hoặc m = -5 Suy ra tổng các giá trị của m là (-5) + 1 = -4

Câu 17: Ta có: 9×2 − 15x + 3 = 0 (a = 9; b = −15; c = 3) ⇒ ∆ = b2 – 4ac = (−15)2 – 4.9.3 = 117 > 0 nên phương trình có hai nghiệm phân biệt.

Câu 18: Ta có: −13×2 + 22x − 13 = 0 (a = −13; b = 22; x = −13) ⇒ ∆ = b2 – 4ac = 222 – 4.(−13). (−13) = −192 < 0 nên phương trình vô nghiệm.