Phân phối chuẩn là gì? Phân phối chuẩn trong tài chính và liên hệ thực tiễn

Trong phân phối chuẩn, dữ liệu được phân phối đối xứng và không bị lệch. Khi được vẽ trên biểu đồ, dữ liệu có dạng hình chuông, với hầu hết các giá trị được nhóm xung quanh một vùng trung tâm và giảm dần khi chúng đi ra xa trung tâm hơn. Phân bố bình thường còn được gọi là phân bố Gaussian hoặc đường cong hình chuông vì hình dạng của chúng.

1. Phân phối chuẩn là gì?

Phân phối chuẩn, còn được gọi là phân phối Gauss, là một phân phối xác suất đối xứng về giá trị trung bình, cho thấy rằng dữ liệu gần giá trị trung bình thường xuất hiện hơn so với dữ liệu xa giá trị trung bình. Ở dạng đồ thị, phân phối chuẩn sẽ xuất hiện dưới dạng đường cong hình chuông.

Phân phối chuẩn là thuật ngữ thích hợp cho đường cong hình chuông xác suất. Trong phân phối chuẩn, giá trị trung bình là 0 và độ lệch chuẩn là 1. Nó có độ lệch 0 và kurtosis là 3. Các phân phối chuẩn là đối xứng, nhưng không phải tất cả các phân bố đối xứng đều bình thường. Trong thực tế, hầu hết các phân phối giá không hoàn toàn bình thường.

Phân phối chuẩn là loại phân phối phổ biến nhất được giả định trong phân tích thị trường chứng khoán kỹ thuật và trong các loại phân tích thống kê khác. Phân phối chuẩn chuẩn có hai tham số: giá trị trung bình và độ lệch chuẩn. Đối với phân phối chuẩn, 68% quan sát nằm trong +/- một độ lệch chuẩn của giá trị trung bình, 95% nằm trong +/- hai độ lệch chuẩn và 99,7% nằm trong + – 3 độ lệch chuẩn.

Mô hình phân phối chuẩn được thúc đẩy bởi Định lý Giới hạn Trung tâm. Lý thuyết này nói rằng các giá trị trung bình được tính toán từ các biến ngẫu nhiên độc lập, có phân phối giống nhau có phân phối xấp xỉ chuẩn, bất kể kiểu phân phối mà các biến được lấy mẫu là gì (miễn là nó có phương sai hữu hạn). Phân phối chuẩn đôi khi bị nhầm lẫn với phân phối đối xứng. Phân phối đối xứng là một trong đó một đường phân chia tạo ra hai hình ảnh phản chiếu, nhưng dữ liệu thực tế có thể là hai bướu hoặc một loạt các ngọn đồi ngoài đường cong hình chuông biểu thị phân phối chuẩn.

Dữ liệu trong cuộc sống thực hiếm khi tuân theo một phân phối chuẩn hoàn hảo. Hệ số độ lệch và hệ số kurtosis đo lường sự khác biệt giữa phân phối nhất định với phân phối chuẩn. Độ lệch đo lường tính đối xứng của một phân phối. Phân phối chuẩn là đối xứng và có độ lệch bằng không. Nếu phân phối của tập dữ liệu có độ lệch nhỏ hơn 0 hoặc độ lệch âm, thì phần đuôi bên trái của phân phối dài hơn phần đuôi bên phải; độ lệch dương ngụ ý rằng phần đuôi bên phải của phân phối dài hơn phần bên trái.

Thống kê kurtosis đo độ dày của các đầu đuôi của một phân phối so với các đuôi của phân phối chuẩn. Các phân phối có kurtosis lớn thể hiện dữ liệu đuôi vượt quá các đuôi của phân phối chuẩn (ví dụ: năm độ lệch chuẩn trở lên so với giá trị trung bình). Các phân phối có tỷ lệ kurtosis thấp thể hiện dữ liệu đuôi thường ít cực đoan hơn so với các đuôi của phân phối chuẩn. Phân phối chuẩn có kurtosis là ba, điều này cho thấy phân phối không có đuôi béo hoặc mỏng. Do đó, nếu một phân phối được quan sát có kurtosis lớn hơn ba, thì phân phối được cho là có nhiều đuôi khi so sánh với phân phối chuẩn. Nếu phân phối có kurtosis nhỏ hơn ba, nó được cho là có đuôi mỏng khi so sánh với phân phối chuẩn.

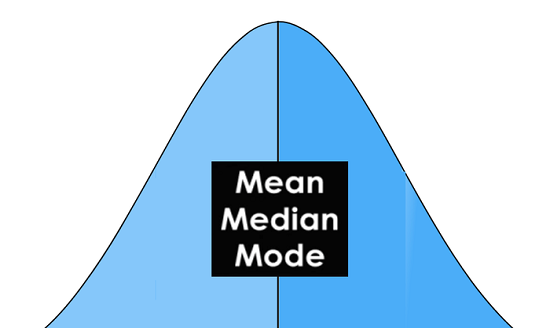
Các phân phối bình thường có các đặc điểm chính dễ nhận thấy trong đồ thị:

– Giá trị trung bình, giá trị trung bình và chế độ hoàn toàn giống nhau.

– Phân phối là đối xứng về giá trị trung bình – một nửa giá trị nằm dưới giá trị trung bình và một nửa trên giá trị trung bình.

– Sự phân phối có thể được mô tả bằng hai giá trị: giá trị trung bình và độ lệch chuẩn.

– Trung bình, trung vị, chế độ và độ lệch chuẩn trong phân phối chuẩn

– Giá trị trung bình là thông số vị trí trong khi độ lệch chuẩn là thông số tỷ lệ.

– Giá trị trung bình xác định nơi tập trung đỉnh của đường cong. Tăng giá trị trung bình sẽ di chuyển đường cong sang phải, trong khi giảm giá trị trung bình sẽ di chuyển đường cong sang trái.

– Phân phối bình thường với các phương tiện khác nhau

– Độ lệch chuẩn kéo dài hoặc ép chặt đường cong. Một độ lệch chuẩn nhỏ dẫn đến một đường cong hẹp, trong khi độ lệch chuẩn lớn dẫn đến một đường cong rộng.

Các phân phối chuẩn có nhiều tính chất thuận tiện, vì vậy các biến thể ngẫu nhiên với các phân bố chưa biết thường được cho là bình thường, đặc biệt là trong vật lý và thiên văn học. Mặc dù đây có thể là một giả định nguy hiểm, nhưng nó thường là một phép gần đúng tốt do một kết quả đáng ngạc nhiên được gọi là định lý giới hạn trung tâm. Định lý này phát biểu rằng giá trị trung bình của bất kỳ tập hợp biến thiên nào với bất kỳ phân phối nào có giá trị trung bình hữu hạn và phương sai có xu hướng theo phân phối chuẩn. Nhiều thuộc tính phổ biến như điểm kiểm tra, chiều cao, v.v., tuân theo phân phối gần như bình thường, với ít thành viên ở đầu cao và thấp và nhiều thành viên ở giữa. Bởi vì chúng xảy ra rất thường xuyên, có một xu hướng đáng tiếc là gọi các phân phối bình thường trong các tình huống mà chúng có thể không áp dụng được.

Như Lippmann đã phát biểu, “Mọi người đều tin vào quy luật sai số theo cấp số nhân: các nhà thí nghiệm, vì họ nghĩ rằng nó có thể được chứng minh bằng toán học; và các nhà toán học, bởi vì họ tin rằng nó đã được thiết lập bằng quan sát” (Whittaker và Robinson 1967, trang 179 ). Trong số các tính chất đáng kinh ngạc của phân phối chuẩn là phân phối tổng chuẩn và phân phối chênh lệch chuẩn có được bằng cách cộng và trừ tương ứng các biến thể X và Y từ hai phân phối chuẩn độc lập với phương tiện và phương sai tùy ý cũng bình thường! Phân phối tỷ lệ chuẩn thu được từ X / Y có phân phối Cauchy.

2. Phân phối chuẩn trong tài chính và liên hệ thực tiễn:

Giả định về phân phối chuẩn được áp dụng cho giá tài sản cũng như hành động giá. Các nhà giao dịch có thể vẽ biểu đồ điểm giá theo thời gian để điều chỉnh hành động giá gần đây thành một phân phối bình thường. Trong trường hợp này, hành động giá càng dịch chuyển từ mức trung bình thì càng có nhiều khả năng tài sản bị định giá cao hơn hoặc thấp hơn. Các nhà giao dịch có thể sử dụng độ lệch chuẩn để đề xuất các giao dịch tiềm năng. Loại giao dịch này thường được thực hiện trên các khung thời gian rất ngắn vì khoảng thời gian lớn hơn khiến việc chọn điểm vào và ra khó hơn nhiều.

Tương tự, nhiều lý thuyết thống kê cố gắng mô hình hóa giá tài sản dưới giả định rằng chúng tuân theo phân phối chuẩn. Trên thực tế, phân bổ giá có xu hướng có đuôi mập và do đó, có kurtosis lớn hơn ba. Những tài sản như vậy đã có biến động giá lớn hơn ba độ lệch chuẩn ngoài giá trị trung bình thường xuyên hơn dự kiến ​​theo giả định có phân phối chuẩn. Ngay cả khi một tài sản đã trải qua một thời gian dài mà nó phù hợp với phân phối chuẩn, thì không có gì đảm bảo rằng hoạt động trong quá khứ thực sự thông báo về triển vọng trong tương lai.

Tất cả các loại biến trong khoa học tự nhiên và xã hội đều có phân phối chuẩn hoặc xấp xỉ chuẩn. Chiều cao, cân nặng khi sinh, khả năng đọc hiểu, mức độ hài lòng trong công việc, hoặc điểm SAT chỉ là một vài ví dụ về các biến số như vậy. Bởi vì các biến phân phối chuẩn rất phổ biến, nhiều phép thử thống kê được thiết kế cho các quần thể phân bố chuẩn. Hiểu các thuộc tính của phân phối chuẩn có nghĩa là bạn có thể sử dụng thống kê suy luận để so sánh các nhóm khác nhau và đưa ra ước tính về dân số bằng cách sử dụng mẫu.

Phân phối chuẩn rất quan trọng trong thống kê và thường được sử dụng trong khoa học tự nhiên và xã hội để biểu diễn các biến ngẫu nhiên có giá trị thực mà phân phối của chúng chưa được biết đến. Tầm quan trọng của chúng một phần là do định lý giới hạn trung tâm. Nó nói rằng, trong một số điều kiện, giá trị trung bình của nhiều mẫu (quan sát) của một biến ngẫu nhiên có giá trị trung bình và phương sai hữu hạn, bản thân nó là một biến ngẫu nhiên – có phân phối hội tụ thành phân phối chuẩn khi số lượng mẫu tăng lên. Do đó, các đại lượng vật lý được mong đợi là tổng của nhiều quá trình độc lập, chẳng hạn như sai số đo, thường có phân bố gần như bình thường.

Hơn nữa, phân bố Gaussian có một số tính chất độc đáo có giá trị trong các nghiên cứu giải tích. Ví dụ: bất kỳ sự kết hợp tuyến tính nào của một tập hợp cố định của các độ lệch chuẩn đều là độ lệch chuẩn. Nhiều kết quả và phương pháp, chẳng hạn như sự lan truyền của độ không đảm bảo và sự phù hợp tham số bình phương nhỏ nhất, có thể được rút ra một cách phân tích ở dạng rõ ràng khi các biến liên quan được phân phối chuẩn. Phân phối chuẩn đôi khi được gọi một cách không chính thức là đường cong hình chuông. Tuy nhiên, nhiều phân bố khác có dạng hình chuông.