Nhị thức bậc nhất là tài liệu vô cùng bổ ích giúp quý độc giả tiết kiệm thời gian và công sức làm việc. Sau đây là nội dung chi tiết mời các bạn cùng tham khảo.
Mục lục bài viết
1. Nhị thức là gì? Nhị thức bậc nhất là gì?
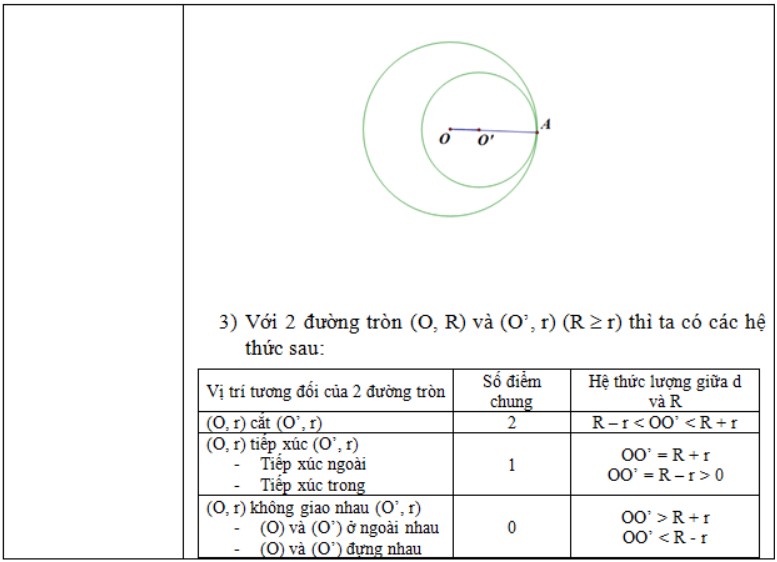
Nhị thức (hay còn được gọi là hệ số nhị thức) là một khái niệm trong toán học, được sử dụng để tính số cách sắp xếp hoặc chọn lọc một số phần tử từ một tập hợp. Ký hiệu của nhị thức là “nCk” hoặc “C(n, k)”, trong đó “n” và “k” là hai số nguyên dương và “n” lớn hơn hoặc bằng “k”.
Nhị thức được tính bằng công thức sau đây:
C(n, k) = n! / (k! * (n – k)!)
Trong đó, “n!” đại diện cho giai thừa của “n”, tức là tích của tất cả các số nguyên dương từ 1 đến “n”.
Nhị thức bậc nhất là nhị thức khi “k” bằng 1, nghĩa là chỉ chọn duy nhất một phần tử từ tập hợp ban đầu. Công thức tính nhị thức bậc nhất là:
C(n, 1) = n! / (1! * (n – 1)!) = n
Nhị thức bậc nhất đơn giản là số phần tử trong tập hợp ban đầu.
2. Lý thuyết về Nhị thức bậc nhất:
Định lý về nhị thức bậc nhất
Ta có biểu thức f(x) = ax + b trong đó a, b là các số thực đã cho trước với điều kiện a # 0. Biểu thức trên là nhị thức bậc nhất một ẩn là x.
Định lý cơ bản về dấu các nhị thức bậc nhất
Cho nhị thức f(x) = ax + b (a #0).
- Dấu của nhị thức cùng dấu với hệ số a khi x lấy giá trị nằm trong khoảng (-b/a; + ∞).
- Dấu của nhị thức trái dấu với hệ số a khi giá trị x thuộc khoảng (- ∞; -b/a).
Ta có bảng xét dấu các nhị thức như sau:

Cách xét dấu tích hoặc thương các biểu thức nhị thức bậc nhất
Cho giá trị F(x) là tích các nhị thức bậc nhất. Áp dụng định lý xét dấu cho các nhị thức bậc nhất, ta có thể xét dấu mỗi thừa số. Lập bảng xét dấu chung cho tất cả các nhị thức F(x) Chúng ta có thể tìm được dấu của F(x). Trường hợp F(x) là một thương số cũng được thực hiện xét dấu tương tự.
Áp dụng lý thuyết ôn tập được vào giải các bất phương trình
Khi giải toán 10 dấu của nhị thức bậc nhất về bất phương trình f(x) > 0 ta xét dấu của biểu thức f(x) xem biểu thức nhận giá trị dương khi nào và biểu thức nhận giá trị âm khi nào.
a) Giải các bất phương trình có chứa ẩn ở mẫu
Cách giải bài toán:
- Xác định điều kiện (ĐKXĐ) của bất phương trình.
- Quy đồng mẫu thức đã cho
- Xét dấu của nhị thức và đưa ra kết luận về tập nghiệm.
b) Giải bài toán về bất phương trình chứa dấu giá trị tuyệt đối
Hãy áp dụng các tính chất của các giá trị tuyệt đối, ta có thể dễ dàng giải các bài toán bất phương trình dạng |f(x)| ≤ a và |f(x)| ≥ a với điều kiện a > 0.
Ta có a > 0:
Nếu |f(x)| ≤ a thì -a ≤ f(x) ≤ a
Nếu |f(x)| ≥ a thì f(x) ≤ -a hoặc giá trị f(x) ≥ a
3. Bài tập về Nhị thức bậc nhất:
3.1. Bài tập 1 – Bài tập về Nhị thức bậc nhất:

a) Biểu thức f(x) = (2x -1) (x +3) đưa về hệ phương trình sau:
2x – 1 = 0 (1) và x + 3 = 0 (2). Giải (1) và (2) ta được:
x1 = ½
x2 = -3
Ta có bảng xét dấu của nhị thức sau:

Từ bảng xét dấu trên ta kết luận:
f(x) < 0 khi -3 < x < ½
f(x) = 0 nếu x = -3 hoặc x = ½
f(x) > 0 nếu x < -3 hoặc x > ½
b) f(x) = (-3x -3) (x + 2)(x + 3)
Ta được hệ phương trình sau:
-3x – 3 = 0 (1)
x + 2 = 0 (2)
x + 3 = 0 (3)
Giải (1), (2) và (3) ta được các nghiệm sau: x1 = -1; x2 = -2; x3 = -3
Ta có bảng xét dấu nhị thức sau:

Vậy ta kết luận được:
f(x) < 0 khi x ∈ (-3; -2) ∪ (-1; + ∞)
f(x) = 0 khi x = -3; x = -2 hoặc x = -1
f(x) > 0 khi x ∈ (- ∞; -3) ∪ ( -2; -1)
c) Biểu thức

Ta có bảng xét dấu nhị thức sau:

Từ bảng xét dấu trên ta kết luận:

d) Ta có: 4x2 -1 = 0 ⇔ (2x -1)(2x +1) = 0
Ta được hệ phương trình:
2x – 1 = 0 (1)
2x + 1 = 0 (2)
Giải (1) và (2) ta được x1 = ½ ; x2 = -½
Ta có bảng xét dấu nhị thức sau:

Từ bảng xét dấu trên ta kết luận được:
f(x) < 0 khi x ∈ (-½ ; ½ )
f(x) > 0 khi x ∈ ( -∞; -½ ) ∪ ( ½ ; +∞)
f(x) = 0 khi x = ± ½
Bài 2: SGK – 94

a) Ta có:

Ta có bảng xét dấu nhị thức sau:
Vậ
b) Ta có:

Ta có bảng xét dấu của nhị thức sau:

Vậy S = (-∞; -1) ∪ (0; 1) ∪ (1; 3) là nghiệm của phương trình trên.
c) Ta có:

Có:
x = 0
x + 12 = 0 ⇔ x = -12
x + 4 = 0 ⇔ x = -4
x + 3 = 0 ⇔ x = -3
Ta có bảng xét dấu nhị thức:
Vậy S = (-12; -4) ∪ (-3; 0) là nghiệm của phương trình trên.
d) Ta có:
Ta có bảng xét dấu của nhị thức trên:

Ta có S= (-1; ⅔ ) ∪ ( 1; + ∞) là nghiệm của phương trình trên.
Bài 3: SGK – 94

a) Bình phương 2 vế ta được:
Ta có bảng xét dấu nhị thức:
Vậy S = ( –∞; -⅖ ] ∪ [2; +∞) là nghiệm của phương trình đã cho.
b) Ta có:
Bảng xét dấu của nhị thức:
Từ bảng xét dấu ta được: x < -5 và x > -1
Kết hợp điều kiện x # -2 và x # 1 ta tìm được S = ( -∞; -5) ∪ (-1; 1) ∪ (1; +∞) là tập nghiệm của phương trình trên.
3.2. Bài tập 2 – Bài tập về Nhị thức bậc nhất:
Bảng sau cho biết dân số của các tỉnh/thành phố Đồng bằng Bắc Bộ năm 2018 (đơn vị triệu người).

a) Tìm số trung bình và trung vị của mẫu số liệu trên.
b) Giải thích tại sao số trung bình và trung vị lại có sự sai khác nhiều.
c) Nên sử dụng số trung bình hay trung vị đại diện cho dân số các tỉnh thuộc Đồng bằng Bắc Bộ?
Lời giải:
Sắp xếp dãy số liệu trên theo thứ tự không giảm, ta được:
0,81; 0,97; 1,09; 1,19; 1,25; 1,27; 1,79, 1,81; 1,85; 2,01; 7,52.
Số trung bình của dãy số liệu trên là:
![]()
Vì n = 11 là một số lẻ nên trung vị là số chính giữa là: Q2 = 1,27.
b) Trong các số liệu có một giá trị bất thường so với các giá trị còn lại là 7,52 do đó ảnh hưởng đến giá trị trung bình của số liệu. Dẫn đến có sự chênh lệch giữa giá trị trung bình và trung vị.
c) Trung bình và trung vị là các thuật ngữ thống kê có vai trò hơi giống nhau trong việc hiểu xu hướng trung tâm của một tập hợp thống kê. Nhưng có giá trị 7,52 là giá trị khác biệt so với các giá trị còn lại nên gây ảnh hưởng đến số trung bình. Do đó ta nên sử dụng số trung vị để đại diện cho dân số các tỉnh thuộc Đồng bằng Bắc Bộ.
Bài 5.25 trang 90 Toán 10 Tập 1: Hai mẫu số liệu sau đây cho biết số lượng trường Trung học phổ thông ở mỗi tỉnh thuộc Đồng bằng Bắc Bộ?
Đồng bằng sông Hồng: 187 34 35 46 54 57 37 39 23 57 27.
Đồng bằng sông Cửu Long: 33 34 33 29 24 39 42 24 23 19 24 15 26.
a) Tính số trung bình, trung vị, các tứ phân vị, mốt, khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn cho mỗi mẫu số liệu trên.
b) Tại sao số trung bình của hai mẫu số liệu có sự sai khác nhiều trong khi trung vị thì không?
c) Tại sao khoảng biến thiên và độ lệch chuẩn của hai mẫu số liệu khác nhau nhiều trong khi khoảng tứ phân vị thì không?
Lời giải:
a) +) Mẫu số liệu đồng bằng sông Hồng:
Số trung bình của mẫu số liệu:

Sắp xếp số liệu trên theo thứ tự không giảm ta được:
23; 27; 34; 35; 37; 39; 46; 54; 57; 57; 187.
Vì n = 11 là số lẻ nên trung bị Q2 = 39.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = 34.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = 57.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 57 – 34 = 23.
Ta có giá trị lớn nhất của số liệu là 187 và giá trị nhỏ nhất là 23. Khi đó khoảng biến thiên là: R = 187 – 23 = 164.
Theo quan sát số liệu, ta thấy giá trị 57 có tần số suất hiện nhiều nhất nên mốt là 57.
+) Mẫu số liệu đồng bằng sông Cửu Long:
Số trung bình của mẫu số liệu:

Sắp xếp số liệu trên theo thứ tự không giảm ta được:
15; 19; 23; 24; 24; 24; 26; 29; 33; 33; 34; 39; 42.
Vì n = 13 là số lẻ nên trung vị Q2 = 26.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = (23 + 24):2 = 23,5.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = (33 + 34):2 = 33,5.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 33,5 – 23,5 = 10.
Ta có giá trị lớn nhất của số liệu là 42 và giá trị nhỏ nhất là 15. Khi đó khoảng biến thiên là: R = 42 – 15 = 27.
Theo quan sát số liệu, ta thấy giá trị 24 có tần số suất hiện nhiều nhất nên mốt là 24.
b) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này làm ảnh hưởng đến giá trị trung bình của mẫu số liệu một nên có sự sai khác nhiều hai số trung bình của hai mẫu số liệu còn trung vị thì không.
c) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này là giá trị lớn nhất nên ảnh hưởng đến khoảng biến thiên của mẫu số liệu một. Trong khi đó, các giá trị của mẫu số liệu hai không có giá trị nào bất thường. Do đó khoảng biến thiên của hai mẫu số liệu có sự chênh lệch nhau.
Độ phân tán của mẫu số liệu một lớn hơn nhiều so với độ phân tán của mẫu số liệu hai. Do đó độ lệch chuẩn của hai số liệu sau có sự khác biệt.
Khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa mà các giá trị chính giữa của hai mẫu số liệu không quá chênh lệch. Do đó khoảng tứ phân vị của hai mẫu số liệu không quá khác biệt.




