Một số bài toán về tỉ số và tỉ số phần trăm | Toán 6 bài 31

1. Tỉ số và tỉ số phần trăm:

– Tỉ số của số a và số b là thương của phép chia a cho b, được viết là a : b (với b khác 0)

Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số hai số đo cùng hai đại lượng đó.

Ví dụ 1:

Tỉ số của 3 và 1/3  là 3 : 1/3

Tỉ số của 1 dm và 1 m là 1 : 10 vì ta phải đổi về cùng đơn vị do đó ta đổi 1 m = 10 dm.

– Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm.

– Tỉ số phần trăm của hai số a và b là  a/b.100%

2. Hai bài toán về tỉ số phần trăm:

Bài 1: Tìm giá trị phần trăm của một số cho trước.

Muốn tìm m % của một số a đã cho ta tính a.m/100

Ví dụ 2: 75% của 48 là

Bài 2: Tìm một số biết giá trị phần trăm của số đó:

Muốn tìm một số khi biết m % của số đó bằng b ta tính b:m/100

Ví dụ 3: 25 % của một số là 6 thì số đó là 6 : 25 % =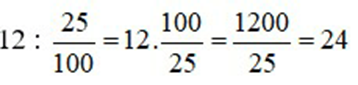

3. Bài tập một số bài toán về tỉ số và tỉ số phần trăm:

Bài 1: Một cửa hàng dự định bán 15 tấn gạo nhưng trên thực tế cửa hàng đã bán được 12 tấn gạo. Hãy cho biết cửa hàng đã thực hiện được bao nhiêu phần trăm kế hoạch?

Lời giải:

Cửa hàng đã thực hiện được số phần trăm kế hoạch là:

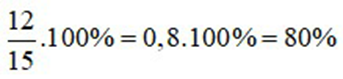
Vậy cửa hàng đã thực hiện được 80% kế hoạch.

Bài 2: Khối lớp 6 của một trường Trung học cơ sở có 150 học sinh, trong đó có 78 học sinh nữ. Hãy

a) Tính tỉ số phần trăm của số học sinh nữ với số học sinh khối 6.

b) Tính số phần trăm của số học sinh nam với số học sinh nữ.

Lời giải:

a) Tỉ số phần trăm của học sinh nữ so với học sinh khối 6 là:

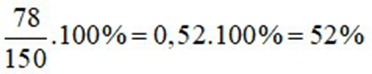
Vậy tỉ số phần trăm của học sinh nữ so với học sinh khối 6 là 52%.

b) Số học sinh nam của khối 6 là:

150 – 78 = 72 (học sinh)

Tỉ số phần trăm của số học sinh nam với số học sinh nữ là:

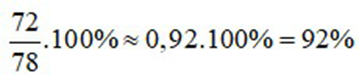
Vậy tỉ số phần trăm của số học sinh nam với số học sinh nữ là 92%.

Bài 3: Một nhà thầu xây dựng nhận xây một ngôi nhà với chi phí là 360 000 000 đồng nhưng chủ nhà xin giảm đi 2, 5 % và nhà thầu đồng ý. Hãy tính số tiền mà nhà thầu nhận xây nhà.

Lời giải:

Số tiền chủ nhà xin giảm với chủ nhà thầu là:

360 000 000 . 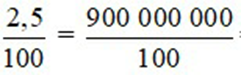  = 9 000 000 (đồng)

Số tiền nhà thầu nhận xây nhà là:

360 000 000 – 9 000 000 = 351 000 000 (đồng)

Vậy số tiền nhà thầu nhận xây nhà là 351 000 000 đồng.

Bài 4: Một lớp có 25 % học sinh giỏi, 55% học sinh khá còn lại là học sinh trung bình. Hãy cho biết số học sinh cả lớp biết số học sinh trung bình là 5 học sinh.

Lời giải:

Tỉ số phần trăm ứng với 5 học sinh trung bình là:

100 % – 25 % – 55 % = 20 %

Số học sinh cả lớp là:

5 : 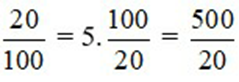   = 25 (học sinh)

Bài 5. Tìm một số biết 35%35% của nó bằng 00,3.

A. 100

B. 60

C. 30

D. 50

Trả lời:

Đổi 35%=35:100=350035%=35:100=3500

Số đó là: 0,3:3500=310.5003=500,3:3500=310.5003=50

Vậy số cần tìm là 50

Đáp án cần chọn là: D

Bài 6. Tỉ số giữa học sinh nam và học sinh nữ là 80%. Hãy tìm số học sinh nam, biết lớp 6A có 36 học sinh?

A. 20 học sinh.

B. 17 học sinh.

C. 19 học sinh.

D. 16 học sinh.

Trả lời:

Đổi 80%=4580%=45, tức là số học sinh nam bằng 4545 số học sinh nữ.

Tổng số phần là:  4 + 5 = 9 (phần)

Lớp 6A có số học sinh nam là:

36 : 9.4 = 16 (học sinh)

Vậy lớp có 16 học sinh nam.

Đáp án cần chọn là: D

Bài 7. Hiệu của hai số là 21. Biết 37,5% số lớn bằng 0,6 số nhỏ. Hãy cho biết số đó là số nào dưới đây?

A. 56; 35

B. 45; 56

C. 60; 39

D. 56; 45

Trả lời:

Đổi 37,5%=38;0,6=3537,5%=38;0,6=35

Tỉ số giữa số lớn và số nhỏ là: 35:38=8535:38=85

Hiệu số phần bằng nhau là:

8 – 5 = 3 (phần)

Số lớn là: 21:3 × 8 = 56

Số nhỏ là: 56 – 21 = 35

Vậy hai số đó là 56; 35

Bài 8: Tìm y biết 2y + 30%y = −2,3?

A. 1

B. 2

C. −1

D. −2

Đáp án cần chọn là: C

Bài 9: Giá niêm yết (chưa bao gồm thuế) của một chiếc tủ lạnh tại 1 cửa hàng điện máy là 6,999 triệu đồng. Hãy cho biết, bác An phải trả bao nhiêu tiền khi mua chiếc tủ lạnh này, biết khi thanh toán bác phải trả thêm thuế VAT, được tính bằng 10% giá niêm yết?

Lời giải chi tiết

Tổng số tiền bác An phải trả là:

6,999 + 6,999.10% = 7,6989 (triệu đồng) = 7 698 900 đồng Bài 10: Nồng độ phần trăm của nước muối là tỉ số phần trăm của số gam muối ăn và số gam nước muối. Hãy cho biết nếu thêm 50 g muối ăn vào 350 g nước muối có nồng độ 10% thì thu được nước muối có nồng độ là bao nhiêu?

Phương pháp giải

+Tính khối lượng muối trong 350 g nước muối ban đầu

+Tính khối lượng muối sau khi thêm 50 g muối

+Tính khối lượng nước muối sau khi thêm 50 g muối

+Nồng độ dung dịch = khối lượng muối : khối lượng dung dịch . 100%

Lời giải chi tiết

Khối lượng muối trong vào 350 g nước muối có nồng độ 10% là:

350 . 10% = 35 (g)

Khối lượng muối sau khi thêm 50 g muối là:

35 + 50 = 85 (g)

Khối lượng dung dịch sau khi thêm 50 g muối là:

350 + 50 = 400 (g)

Nồng độ phần trăm nước muối sau khi thêm 50 g muối là:

85400.100%=21,25%

Bài 11: Khi mua một chiếc điện thoại di động với giá 3 290 000 đồng, người mua có thể thanh toán toàn bộ số tiền 3 290 000 đồng hoặc trả trước 36% giá bán chiếc điện thoại và trả góp trong 6 tháng, mỗi tháng 360 000 đồng. Hãy cho biết, trả theo cách nào người mua phải trả nhiều tiền hơn?

Phương pháp giải

Tính số tiền phải trả khi trả góp rồi so sánh với giá 3 290 000 đồng

Lời giải chi tiết

Số tiền phải trả khi trả góp là:

3 290 000 . 36% + 6. 360 000 = 3 344 400 (đồng)

Vì 3 344 400 > 3 290 000 nên khi trả góp người mua phải trả nhiều tiền hơn

Bài 12: Một thanh đồng dài 4,6 m. Khi đem thanh đồng này nung nóng thì đồng giãn nở và chiều dài thanh tăng 1,2%. Hãy tính chiều dài thanh đồng sau khi được nung nóng.

Phương pháp giải

Tính chiều dài thanh đồng tăng thêm

Tính chiều dài thanh đồng sau khi được nung nóng.

Lời giải chi tiết

Chiều dài thanh đồng tăng thêm là:

4,6 . 1,2% = 0,0552 (m)

Chiều dài thanh đồng sau khi được nung nóng là:

4,6 + 0,0552 = 4,6552 (m)

Bài 13: Một tảng thịt khi lấy từ ngăn đá ra có cân nặng 2,5 kg. Sau khi rã đông, khối lượng của tảng thịt giảm 7%. Hãy cho biết khối lượng tảng thịt sau khi rã đông?

Phương pháp giải

Tính khối lượng giảm

Tính khối lượng tảng thịt sau khi rã đông

Lời giải chi tiết

Khối lượng của tảng thịt giảm:

2,5 . 7% = 0,175 (kg)

Khối lượng tảng thịt sau khi rã đông là:

2,5 – 0,175 = 2,325(kg)

Bài 14: Sau khi đóng băng, thể tích nước đá tăng 9%. Hãy cho biết đóng băng 275 cm3 nước thành nước đá thì khối nước đá có thể tích là bao nhiêu xentimet khối?

Phương pháp giải

Tính thể tích tăng thêm =  thể tích ban đầu . 9%

Tính thể tích sau khi đóng băng =  thể tích ban đầu + thể tích tăng thêm

Lời giải chi tiết

Thể tích tăng thêm là:

275. 9% = 24,75 (cm3)

Thể tích sau khi đóng băng là:

275 + 24,75 = 299, 75 (cm3)

Bài 15: Biển Chết (Dead Sea) là tên gọi của một hồ nước mặn ở Israel. Nước trong hồ này có độ mặn rất cao, trong mỗi lít nước có chứa tới 350 gam muối. Vì nước mặn như thế nên cá hay các loài thủy sinh vật lớn không thể sống trong nước Biển Chết (đó chính là lí do hồ có tên gọi là “ Dead Sea”). Cũng chính bởi độ mặn mà con người có thể nổi bồng bềnh trong nước Biển Chết. Hãy cho biết nồng độ phần trăm muối trong nước hồ Biển Chết là bao nhiêu.

Phương pháp giải

Đổi lít nước sang gam nước

Tính nồng độ phần trăm muối trong nước hồ Biển Chết

Lời giải chi tiết

Đổi 1 lít nước = 1000 ml nước = 1000 g nước

Nồng độ phần trăm muối trong nước hồ Biển Chết là:

3501000.100%=35%”>3501000.100%=35%