Toán học vecto là một trong những kiến thức hay và khó buộc các bạn học sinh lớp 10 phải học tập và hiểu bản chất vấn đề. Nhằm giúp các bạn học sinh có thêm tư liệu học tập, chúng tôi xin gửi tới bạn đọc Lý thuyết Tích vô hướng của hai vectơ chi tiết -Toán lớp 10. Mời các bạn tham khảo nhé.
Mục lục bài viết
1. Lý thuyết Tích vô hướng của hai vecto chi tiết:
Định nghĩa:


Biểu thức tọa độ tích vô hướng và hệ quả:
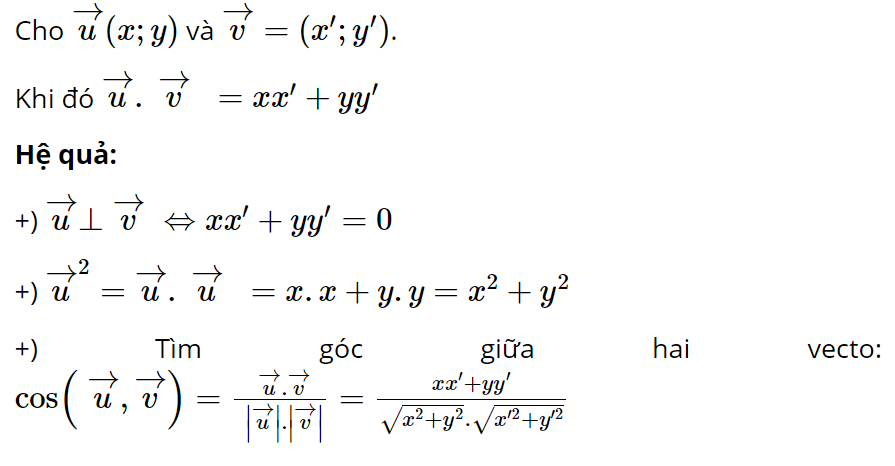
Các tính chất của tích vô hướng vecto:
Người ta chứng minh được các tính chất sau đây của tích vô hướng:
Hệ quả:
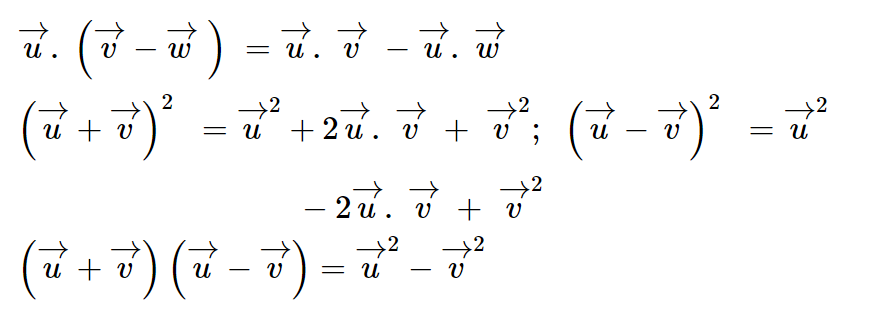
Biểu thức tọa độ của tích vô hướng:

Ứng dụng:
a, Tính độ dài vecto. Độ dài vecto a(a1,a2) được tính theo công thức:

Công thức tính tích vô hướng khi biết độ dài:

b, Góc giữa hai vec tơ: Từ định nghĩa tích vô hướng của hai vec tơ ta suy ra nếu:
* Các trường hợp đặc biệt:

c, Khoảng cách giữa hai điểm: Khoảng cách giữa hai điểm A(xA; yA), B(xB;yB) được tính theo công thức:

2. Cách tiếp cận bài học dành cho học sinh lớp 10 về vecto:
KẾ HOẠCH DẠY HỌC
I. MỤC TIÊU CỦA BÀI:
1. Kiến thức:
+) Nắm được định nghĩa tích vô hướng của hai vectơ, tính chất, ứng dụng, ý nghĩa vật lý và biểu thức tọa độ của nó.
+) Kiến thức : Củng cố các kiến thức về véctơ, hai véctơ bằng nhau, tổng hiệu của hai véctơ, tích của một véctơ với một số, tích vô hướng của hai véctơ, biểu thức tọa độ của các phép toán vectơ.
+) Kĩ năng : Áp dụng các kiến thức đã học để giải quyết một số bài tập về biểu diễn vectơ, chứng minh đẳng thức vectơ, chứng minh ba điểm thẳng hàng, chứng minh hai đường thẳng vuông góc, tìm tọa độ điểm, tọa độ của vectơ… Biểu thị được một số đại lượng trong thực tiễn bằng vectơ. Sử dụng được vectơ và các phép toán trên vectơ để giải thích một số hiện tượng có liên quan đến Vật lí. Vận dụng được kiến thức về vectơ để giải một số bài toán hình học và một số bài toán liên quan đến thực tiễn.
2. Kỹ năng:
Tính được tích vô hướng của hai vectơ bằng định nghĩa và bình phương vô hướng, bằng biểu thức tọa độ cũng như ứng dụng của nó vào việc tính độ dài của đoạn thẳng, góc giữa hai vectơ. Biết được cách chứng minh hai vectơ vuông góc.
3. Thái độ:
Nghiêm túc trong học tập, có tinh thần làm việc nhóm, hỗ trợ nhau trong học tập.
4. Định hướng phát triển năng lực:
Phát huy năng lực tự học, năng lực hợp tác trong học tập, năng lực vận dụng kiến thức khoảng cách vào thực tế như tính góc nhìn tú thực tế, đo đạc khoảng cách giữa ngọn núi, chiều rộng của con sông….
Thực hiện và hoàn thành tốt các nhiệm vụ năm học, giúp học sinh ôn tập tốt các đơn vị kiến thức và có các kĩ năng làm bài.
5. Cách thức tiếp cận:
Dựa vào đặc điểm tình hình của học sinh để đưa ra hệ thống các bài tập phù hợp. Trong một tiết dạy có khoảng 80% số bài tập vừa sức với tất cả học sinh, còn lại 20% số bài tập nâng cao hơn dành cho học sinh khá giỏi.
II. Chuẩn bị của giáo viên và học sinh
1. Giáo viên:
Bảng phụ, thước kẻ, compa, kết quả các hoạt động
2. Học sinh:
Sách giáo khoa, tinh thần sẵn sàng hợp tác trong học tập, trao đổi…
III. Chuỗi các hoạt động học
1. GIỚI THIỆU (HOẠT ĐỘNG TIẾP CẬN BÀI HỌC)
Kiểm tra bài cũ
2. NỘI DUNG BÀI HỌC (HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC)
Hoạt động 1: Góc giữa hai vectơ
a) Mục tiêu:
– HS có cơ hội trải nghiệm, thảo luận về góc giữa hai vectơ.
– Nhận biết khái niệm góc giữa hai vectơ và thực hành tìm góc giữa hai vectơ rèn luyện kĩ năng theo yêu cầu cần đạt.
b) Nội dung: HS thực hiện lần lượt các hoạt động dưới sự điều hành của GV để tiếp nhận kiến thức về góc giữa hai vectơ.
c) Sản phẩm: HS hình thành được kiến thức bài học, hoàn thành được các bài HĐKP1; Ví dụ 1; Thực hành 1.
d) Tổ chức thực hiện:
Bước 1: GV chuyển giao nhiệm vụ:
– GV cho HS thảo luận nhóm bốn thực hiện HĐKP 1.
– GV dẫn dắt, giới thiệu, đặt câu hỏi thêm:
+ Số đo góc IDC cũng được gọi là số đo góc giữa hai vectơ và .
+ GV yêu cầu HS tìm số đo các góc giữa hai vectơ và .
– GV dẫn dắt, giới thiệu góc giữa hai vectơ như trong khung kiến thức:
– GV mời một vài HS đọc khung kiến thức trọng tâm.
– GV nhấn mạnh:
Cách xác định góc giữa hai vectơ không phụ thuộc vào việc chọn điểm O, nên góc giữa hai vectơ
– GV đặt câu hỏi thêm: Khi nào thì góc giữa hai vectơ bằng 0o, bằng 180o?
– GV lưu ý cho HS các Chú ý trong SGK:
+ Từ định nghĩa ta có
+ Góc giữa hai vectơ ngược hướng và khác luôn bằng 180o.
+ Trong trường hợp có ít nhất một trong hai vectơ và là vectơ
– HS đọc Ví dụ 1, GV hướng dẫn, HS tự thực hiện và vở cá nhân sau đó trao đổi cặp đôi kiểm tra chéo đáp án.
– HS áp dụng làm Thực hành 1, thực hành tìm góc giữa hai vectơ để rèn luyện kĩ năng theo yêu cầu..
Bước 2: HS thực hiện nhiệm vụ học tập:
– HS suy nghĩ để trả lời các vấn đề được đưa ra.
– HS suy nghĩ, đọc SGk.
– GV hỗ trợ, quan sát.
Bước 3: Báo cáo kết quả hoạt động, thảo luận:
– Một số HS khác nhận xét, bổ sung cho bạn.
– HS trả lời câu hỏi của GV để xây dựng bài.
Bước 4: Đánh giá kết quả thực hiện:
GV nêu nhận xét, tổng quát lại kiến thức cần nhớ về góc giữa hai vectơ.
Kết quả cần đạt:
1. Góc giữa hai vectơ
Góc với số đo từ 0o đến 180o được gọi là góc giữa hai vectơ và .
Ta kí hiệu góc giữa hai vectơ
Nếu góc là 90o thì ta nói rằng và vuông góc với nhau, kí hiệu
* Chú ý:
– Từ định nghĩa ta có:
– Góc giữa hai vectơ ngược hướng và khác luôn bằng 180o.
– Trong trường hợp có ít nhất một trong hai vectơ và là vectơ
Ví dụ 1: SGK-tr98
Thực hành 1.
Lấy điểm D sao cho AD // BC và AD = BC
3. Những phương pháp giúp học sinh học tốt môn Toán vecto lớp 10:
Véc – tơ là một trong những khái niệm cơ bản trong Toán học đương đại và có ứng dụng không chỉ trong lĩnh vực Toán học mà còn trong nhiều lĩnh vực khác như Vật lí, Kỹ thuật, và nhiều ngành khoa học khác. Trong chương trình học hình học hiện nay, việc hiểu và áp dụng véc – tơ là vô cùng quan trọng. Tuy nhiên, nhiều học sinh gặp khó khăn khi học phần này.
Khi áp dụng phương pháp véc – tơ, nhiều học sinh thường gặp khó khăn, không biết bắt đầu từ đâu và thường mắc sai lầm. Thêm vào đó, việc hiểu rõ hai khái niệm quan trọng về độ dài và định hướng của véc – tơ cũng đôi khi khá phức tạp, do véc – tơ thường không thể thấy bằng mắt, điều này làm cho việc hình dung và hiểu ý nghĩa hình học trở nên khó khăn.
Để thành công trong việc học Toán hình học lớp 10, bạn cần tuân thủ một số nguyên tắc quan trọng:
Hiểu chắc lý thuyết: Để giải quyết bài tập Toán hình học, bạn cần nắm vững kiến thức lý thuyết, định nghĩa, và định lý. Hãy đọc trước bài mới trước khi đến lớp, lắng nghe giảng và ghi chép kỹ lưỡng. Nếu có bất kỳ điểm gì bạn không hiểu, hãy đặt câu hỏi cho thầy cô hoặc bạn bè để nhận được giải đáp đúng lúc.
Làm nhiều bài tập: Sau khi đã nắm vững lý thuyết, bạn cần thực hành bằng cách làm nhiều bài tập. Bắt đầu với các ví dụ trong sách giáo khoa phù hợp với từng phần lý thuyết, sau đó hoàn thành tất cả các bài tập trong sách giáo khoa. Nếu bạn muốn nâng cao kiến thức, hãy thực hiện các bài tập ở các sách tham khảo cao cấp để rèn luyện kỹ năng giải quyết vấn đề.
Lựa chọn sách tham khảo: Trên thị trường có nhiều loại sách tham khảo khác nhau, và việc lựa chọn đúng loại sách rất quan trọng. Hãy ưu tiên lựa chọn các sách từ các nhà xuất bản và tác giả có uy tín. Chọn sách tập trung vào chủ đề bạn đang học, với nội dung tổng hợp kiến thức lý thuyết, ví dụ minh họa rõ ràng và lời giải dễ hiểu. Những cuốn sách tham khảo này sẽ giúp bạn nắm bắt kiến thức Toán hình học lớp 10 một cách hiệu quả
Các bước tìm hiểu bài toán vecto giúp các bạn học sinh học tốt:
Bước 1: Tìm hiểu nội dung bài toán cẩn thận.
Bước 2: Xây dựng kế hoạch giải quyết bài toán.
Bước 3: Thực hiện kế hoạch giải quyết bài toán.
Bước 4: Kiểm tra và nghiên cứu lại lời giải.
Trong quá trình học, học sinh cần nắm vững những khái niệm cơ bản như Véc – tơ, hai Véc – tơ bằng nhau, hai Véc – tơ đối nhau, và nhiều khái niệm khác liên quan. Họ cũng cần hiểu về các quy tắc và tính chất cơ bản như phép cộng, phép trừ, phép nhân Véc – tơ với một số thực, tích vô hướng của hai Véc – tơ, và nhiều quy tắc khác.
Kỹ năng cơ bản khi giải bài toán Véc – tơ bao gồm việc xây dựng Véc – tơ từ thông tin có sẵn, áp dụng các quy tắc hình học và quy tắc ba điểm để xây dựng Véc – tơ tổng, cũng như giải quyết các bài toán thực tế liên quan. Để phát triển kỹ năng này, học sinh cần thực hành giải nhiều bài tập khác nhau, từ dễ đến khó, và sắp xếp chúng một cách hợp lý.




