Dưới đây là bài viết về chủ đề: Lý thuyết Phương trình đường thẳng và các dạng bài ôn tập từ cơ bản đến nâng cao giúp chúng ta hiểu rõ hơn về các thuộc tính và ứng dụng của hàm số trong giải toán, mời bạn đọc theo dõi.
Mục lục bài viết
1. Lý thuyết Phương trình đường thẳng và các dạng bài :
Vecto chỉ phương của đường thẳng
Ta có vector u được gọi là vectơ chỉ phương của đường thẳng ∆ nếu vectơ u ≠ vectơ 0 và giá của vectơ u song song hoặc trùng với ∆. Từ lý thuyết trên ta có thể thấy được một đường thẳng sẽ có vô số vectơ chỉ phương trong mặt phẳng không gian.
Phương trình tham số của đường thẳng
Đường thẳng ∆ đi qua điểm M0(x0, y0) và có vectơ chỉ phương u = (a; b)
Vậy ta có phương trình tham số của đường thẳng ∆ đã cho có dạng:
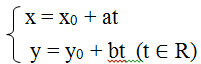
Nhận xét: Nếu đường thẳng ∆ có Vectơ chính phụ = (a; b)
thì có hệ số góc được tính theo công thức:
k = b/a
Véctơ pháp tuyến của đường thẳng:
Ta có vector n được gọi là vectơ chỉ phương của đường thẳng ∆ nếu vectơ n ≠ vectơ 0 và giá của vectơ n vuông góc với đường thẳng ∆. Như vậy, tương tự như vectơ chỉ phương, một đường thẳng sẽ có vô số vectơ chỉ phương.
Mối quan hệ giữa vectơ pháp tuyến và vectơ chỉ phương:
Viết phương trình tổng quát của đường thẳng trên trục tọa động
Đường thẳng ∆ đi qua điểm M0(x0, y0) và có Vectơ pháp tuyến n = (A; B)
=> phương trình tổng quát của đường thẳng ∆ có dạng
A(x – x0) + B(y – y0) = 0 hay Ax + By + C = 0 với C = –Ax0 – By0
Đây là cách viết phương trình tổng quát của đường thằng khi các bạn làm bài tập của các dạng này.
Lưu ý:
+) Nếu đường thẳng ∆ có VTPT n = (A; B) thì có hệ số góc:
k = -a/b
+) Nếu A, B, C đều khác 0 thì ta có thể đưa phương trình tổng quát của đường thẳng về dạng:
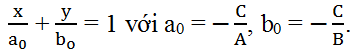
Phương trình trên được gọi là phương trình đường thẳng theo đoạn chắn, đường thẳng này cắt 2 trục tọa độ Ox và Oy lần lượt tại các điểm M(a0; 0) và N(0; b0).
Vị trí tương đối của hai đường thẳng
Xét hai đường thẳng có phương trình tổng quát là
∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0
Tọa độ giao điểm của ∆1 và ∆2 là nghiệm của hệ phương trình:
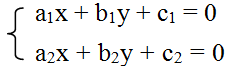
+) Nếu hệ có một nghiệm duy nhất (x0; y0) thì đường thẳng ∆1 cắt ∆2 tại một điểm điểm M0(x0, y0).
+) Nếu hệ trên có vô số nghiệm nghĩa là ∆1 trùng với ∆2.
+) Nếu hệ vô nghiệm thì đường thẳng ∆1 và ∆2 không có điểm chung, hay ∆1 song song với ∆2
Cách 2. Xét tỉ số
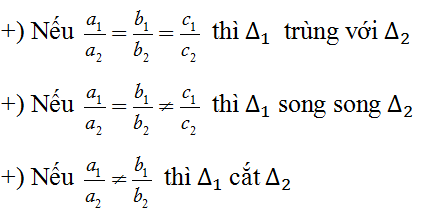
Góc giữa hai đường thẳng
Cho hai đường thẳng
∆1: a1x + b1y + c1 = 0 có VTPT n1 = (a1; b1);
∆2: a2x + b2y + c2 = 0 có VTPT n2 = (a2; b2);
Gọi α là góc tạo bởi giữa hai đường thẳng ∆1 và ∆2
Khi đó ta có:
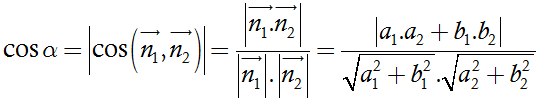
Khoảng cách từ một điểm đến một đường thẳng
Khoảng cách từ điểm M0(x0, y0) đến đường thẳng ∆: ax + by + c = 0 được tính theo công thức như sau:
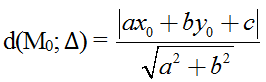
Nhận xét: Cho hai đường thẳng ∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0 giao nhau. Ta tìm phương trình hai đường phân giác của góc tạo bởi hai đường thẳng trên là:
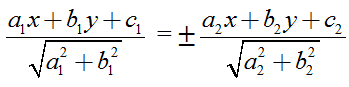
2. Cách làm Phương trình đường thẳng:
Để làm được bài toán này ta thực hiện như sau:
Bước 1. Xác định hàm số y = ax + b biết hệ số góc a và đồ thị của nó đi qua điểm A(m; n)
+ Thay hệ số góc vào hàm số
+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta sẽ tìm được b
Bước 2. Đồ thị của hàm số y = ax + b song song với đường thẳng y = a’x + b’ và đi qua A(m; n)
+ Đồ thị hàm số y = ax + b song song với đường thẳng y = a’x + b’ nên a = a’
+ Thay a = a’ vào hàm số
+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta sẽ tìm được b
Bước 3. Đồ thị của hàm số y = ax + b vuông góc với đường thẳng y = a’x + b’ và đi qua A(m; n)
+ Đồ thị hàm số y = ax + b vuông góc với đường thẳng y = a’x + b’ nên a.a’ = -1 sau đó thay a vừa tìm được vào hàm số
+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta sẽ tìm được b
Bước 4. Đồ thị của hàm số y = ax + b đi qua hai điểm A(m; n) và B(p; q)
+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta được phương trình thứ nhất
+ Vì đồ thị của nó đi qua B(p; q) nên thay x = p và y = q vào hàm số ta được phương trình thứ hai
+ Giải hệ phương trình gồm hai phương trình trên ta sẽ tìm được a và b
Bước 5. Đồ thị của hàm số y = ax + b đi qua A(m; n) và cắt trục hoành tại điểm có hoành độ bằng c
+ Đồ thị hàm số y = ax + b cắt trục hoành tại điểm có hoành độ bằng c nên nó đi qua điểm B(0; c)
+ Bài toán trở thành viết phương trình đường thẳng biết đồ thị hàm số đi qua hai điểm A(m; n) và B(0; c)
Bước 6. Đồ thị của hàm số y = ax + b đi qua A(m; n) và cắt trục tung tại điểm có tung độ bằng c
+ Đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ bằng c nên nó đi qua điểm B(c; 0)
+ Bài toán trở thành viết phương trình đường thẳng biết đồ thị hàm số đi qua hai điểm A(m; n) và B(c; )
3. Bài ôn tập về Phương trình đường thẳng:
Bài 1: Cho đường thẳng d cắt trục Ox, Oy tại hai điểm A(0; 5) và B(6; 0). Viết phương trình tổng quát và phương trình đoạn chắn của đường thẳng d.
Lời giải:
Vì A(0; 5) và B(6; 0) thuộc đường thẳng d nên ta có 
là vectơ chỉ phương của đường thẳng d.
= (6-0;0-5) = (6;-5)
Vectơ pháp tuyến của d là 
(5;6)
Chọn điểm A(0; 5) thuộc đường thẳng d, ta có phương trình tổng quát của đường thẳng d:
5.(x – 0) + 6.(y – 5) = 0
5x + 6y – 30 = 0
Vì đường thẳng d cắt trục Ox, Oy lần lượt tại hai điểm A(0; 5) và B(6; 0) nên ta có phương trình đoạn chắn: 
= 1.
Bài 2: Cho đường thẳng d đi qua hai điểm M(5; 8) và N(3; 1). Viết phương trình tham số và phương trình chính tắc của đường thẳng d.
Lời giải:
Vì M(5; 8) và N(3; 1) thuộc đường thẳng d nên ta có 
là vectơ chỉ phương của đường thẳng d, có = (3 – 5; 1 – 8) = (-2; -7)
Chọn điểm N(3; 1) thuộc đường thẳng d ta có phương trình tham số của đường thẳng d: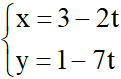 
Chọn điểm M(5; 8) thuộc đường thẳng d ta có phương trình chính tắc của đường thẳng d: 
Bài 3: Xét vị trí tương đối của hai đường thẳng sau:
a) d1: 4x – 10y + 1 = 0 và d2 : x + y + 2 = 0.
b) d3: 12x – 6y + 10 = 0 và d4 : 2x – y + 5 = 0.
c) d5: 8x + 10y – 12 = 0 và d6 : 4x + 5y – 6 = 0.
Lời giải:
a) Xét hai đường thẳng d1: 4x – 10y + 1 = 0 và d2 : x + y + 2 = 0 có:
d1 và d2 cắt nhau.
b) Xét hai đường thẳng d3: 12x – 6y + 10 = 0 và d4 : 2x – y + 5 = 0 có:
= 6 # 
= 2 => d3//d4
c) Xét hai đường thẳng d5: 8x + 10y – 12 = 0 và d6 : 4x + 5y – 6 = 0 có:
= 2 => d5 
d6
Bài 4: Cho hai đường thẳng: d1: x – 2y + 5 = 0 và d2 : 3x – y = 0. Tìm tọa độ giao điểm của d1 và d2.
Lời giải:
Xét tỉ số: 
=> d1 
d2 . Gọi tọa độ giao điểm của d1 và d2 là M(x; y) với x và y là nghiệm của hệ phương trình:
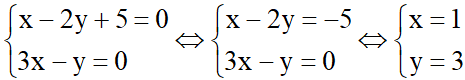
Vậy d1 d2 tại M (1; 3).
