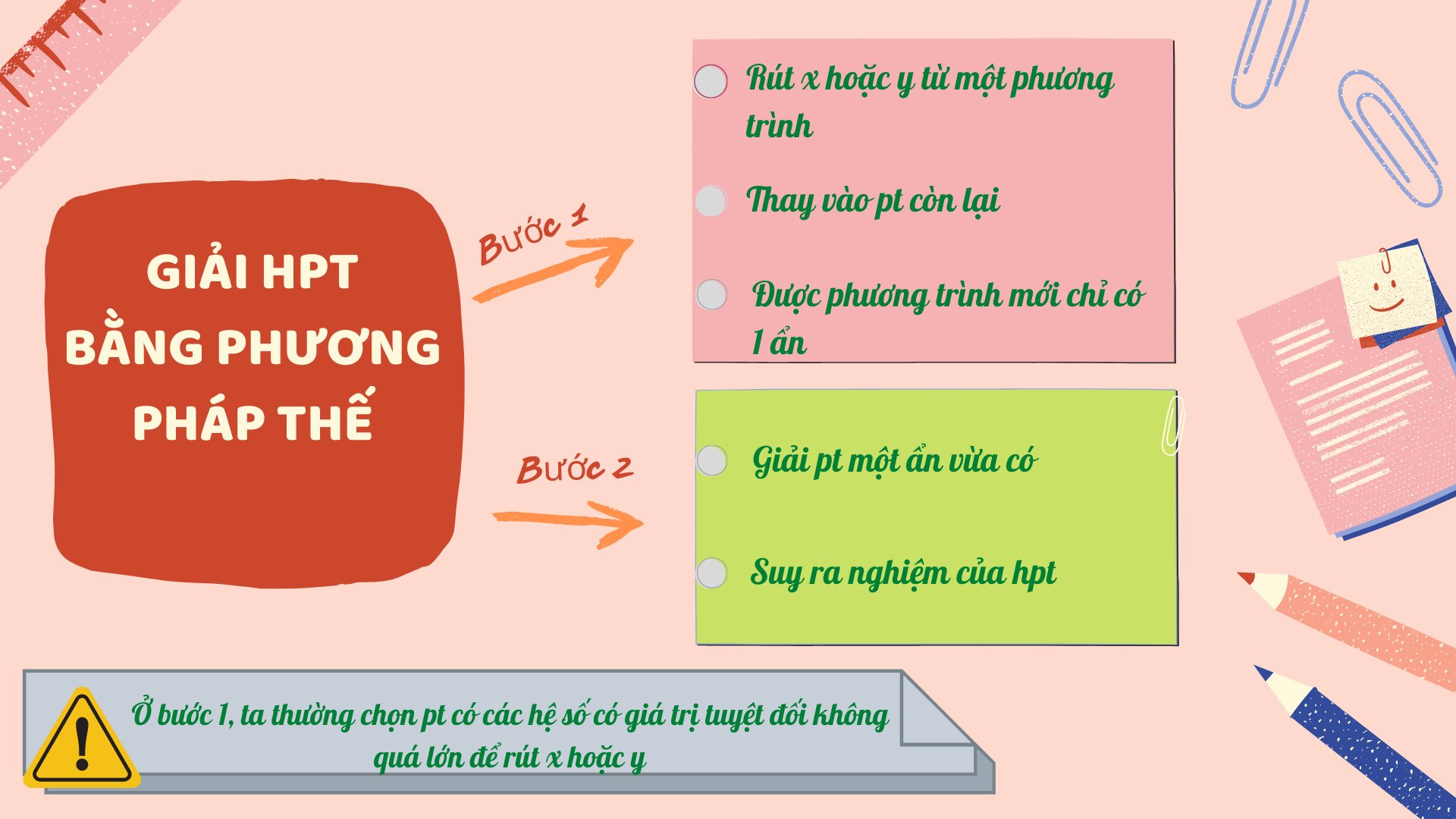
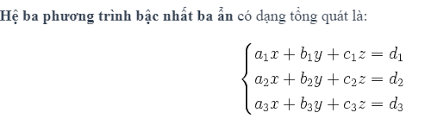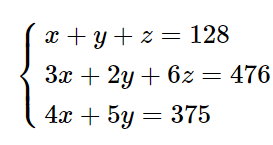Mục lục bài viết
1. Hướng dẫn giải hệ phương trình đối xứng hai ẩn lớp 9 loại 1:
a. Dạng của hệ phương trình
– là một loại hệ phương trình đặc biệt, với đặc điểm là khi hoán đổi giữa hai ẩn x và y trong mỗi phương trình của hệ, thì hệ vẫn giữ nguyên dạng ban đầu. Để hiểu rõ hơn về hệ phương trình đối xứng loại 1 và cách giải, chúng ta có thể xem xét ví dụ sau.
– Ví dụ: Hệ phương trình
Khi thay x bởi y và thay y bởi x thì được hệ
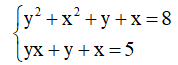
Ta thấy mỗi phương trình của hệ không thay đổi nên hệ đã cho là hệ đối xứng loại 1
b. Cách giải
Bước 1: Biến đổi biểu thức ở hai phương trình của hệ theo tổng và tích của x, y
Bước 2: Đặt 
với điều kiện (S^2 ≥ 4P)
Bước 3: Tìm S, P thỏa mãn điều kiện (S^2 ≥ 4P). Khi đó x, y là nghiệm của phương trình t^2 – Sx + P = 0
Bước 4: Kết luận
Ví dụ: giải hệ phương trình
Giải
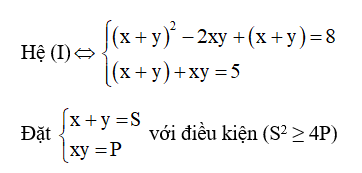
Từ S + P = 5 ⇒ P = 5 – S. Thế vào phương trình S^2 + S -2P = 8 ta được
* Với S = 3 ⇒ P = 5 – 3 = 2 thỏa mãn điều kiện (S^2 ≥ 4P)
Ta có 
, theo Vi-et x, y là nghiệm của phương trình:
Suy ra hệ có hai nghiệm: x = 1 và y = 2, x =2 và y = 1
* Với S = -6 ⇒ P = 5 – (-6) = 11 không thỏa mãn điều kiện (S^2 ≥ 4P) nên loại
Vậy hệ đã cho có hai nghiệm: x = 1 và y = 2, x =2 và y = 1
2. Hướng dẫn giải hệ phương trình đối xứng hai ẩn lớp 9 loại 2:
a. Dạng của hệ phương trình
– Là hai phương trình hai ẩn x và y, trong đó, mỗi phương trình khi hoán đổi giữa x và y sẽ trở thành phương trình kia và ngược lại, nhưng hệ không thay đổi. Điều này có thể được minh họa bằng ví dụ sau:
– Ví dụ: Hệ phương trình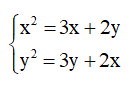 
Khi thay x bởi y và thay y bởi x thì được hệ 
Ta thấ
b. Cách giải
– Bước 1: Trừ vế với vế của hai phương trình cho nhau ta được phương trình dạng
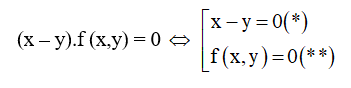
-Bước 2: Kết hợp (*) với 1 phương trình của hệ, kết hợp (**) với 1 phương trình của hệ ta được hai hệ phương trình. Giải hai hệ phương trình đó
-Bước 3: Kết luận
Ví dụ: 
Giải
Lấy (1) – (2) ta được:
Kết hợp x – y = 0 với phương trình (1) ta có hệ:
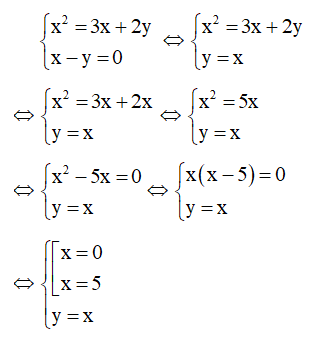
Với x = 0 thì y = x = 0
Với x = 5 thì y = x = 5
Kết hợp x + y – 1 = 0 với phương trình (1) ta có hệ:
Với x = -1 thì y = 1 – x = 1 + 1 = 2
Với x = 2 thì y = 1 – x = 1 – 2 = -1
Vậy hệ phương trình có 4 nghiệm : (0;0), (5;5), (-1;2), (2;-1)
3. Bài tập có đáp án:
Câu 1: Hệ phương trình sau có bao nhiêu nghiệm: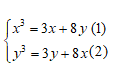 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
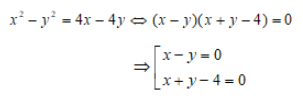
TH1: x = y. Thay x = y vào phương trình (1) ta sẽ có:
x^2 = 3x – x = 0
<=> x^2 – 12x = 0
<=> x (x – 12) = 0
TH2: Ta có phương trình sau:
x + y – 4 = 0. Thay y = 4 – x vào phương trình (1) ta được:
x^2 – 4x + 4 = 0 <=> (x – 2) ^2 = 0 =>x = 2
Với x = 2 ⇒ y = 2. Suy ra hệ có nghiệm là: (2;2)
Vậy hệ phương trình có 2 nghiệm là: (0;0), (2;2).
Chọn đáp án B.
Câu 2: Hệ phương trình sau có bao nhiêu nghiệm: Cách giải hệ phương trình đối xứng loại 2 cực hay | Toán lớp 9
A. 4
B. 2
C. 3
D. 5
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
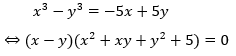
TH1: x – y = 0. Thay x = y vào phương trình (1) ta sẽ có:
x^3 = 3x + 8x = 0
<=> x^3 – 11x = 0
<=> x (x^2 – 11) = 0
TH2: Ta có phương trình như sau:
Chọn đáp án C.
Câu 3: Hệ phương trình dưới đây có bao nhiêu nghiệm: 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Suy ra hệ có 2 nghiệm (2;-1); (-1;2)
Vậy hệ phương trình có 4 nghiệm là:
(0;0), (5;5), (2;-1), (-1;2).
Chọn đáp án đúng là D.
Câu 4: Hệ phương trình sau có bao nhiêu nghiệm: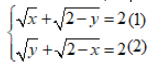 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn chi tiết:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Với x = 1 ⇒ y = 1. Suy ra hệ có nghiệm là: (1; 1),
Vậy hệ phương trình có 1 nghiệm là: (1;1).
Chọn đáp án A.
Câu 5: Hệ phương trình sau có bao nhiêu nghiệm: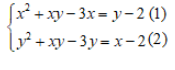 
A. 4
B. 3
C. vô số nghiệm
D. vô nghiệm
Lời giải:
Hướng dẫn chi tiết:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Vậy hệ phương trình có vô số nghiệm là: (x ∈ R, y = 2 – x).
Chọn đáp án C.
Câu 6: Hệ phương trình sau: 
Khẳng định nào sau đây đúng ?
A. Hệ phương trình có vô số nghiệm.
B. Hệ phương trình có 3 nghiệm.
C. Hệ phương trình có 4 nghiệm.
D. Hệ phương trình có 1 nghiệm.
Lời giải:
Hướng dẫn chi tiết:
Đk: x ≠ 0, y ≠ 0
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
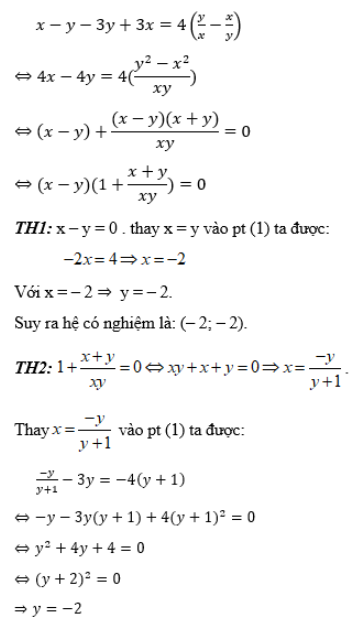
Với y = –2 ⇒ x = –2 ™. Suy ra hệ có nghiệm là: (– 2; – 2).
Vậy hệ phương trình có 1 nghiệm là: (– 2; – 2).
Chọn đáp án D.
Câu 7: Hệ phương trình sau: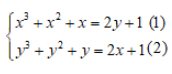 
. Khẳng định nào sau đây đúng ?
A. Hệ phương trình có vô số nghiệm.
B. Hệ phương trình có 2 nghiệm.
C. Hệ phương trình có 4 nghiệm.
D. Hệ phương trình có 3 nghiệm.
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
x3 – y3 + x^2 – y^2 + x – y = 2y – 2x
⇔ (x – y)(x^2 + xy + y^2 ) + (x – y)(x + y) + 3(x – y) = 0
⇔ (x – y)(x^2 + y^2 + xy + x + y + 3) = 0
TH1: x – y = 0 . thay x = y vào pt (1) ta được:
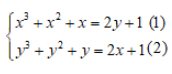
Với x = – 1 ⇒ y = – 1 và x = 1 ⇒ y = 1. Suy ra hệ có 2 nghiệm là: (– 1; – 1), (1;1).
TH2: x^2 + y^2 + xy + x + y + 3 = 0 ⇔ x^2 + (y + 1)x + y^2 + y + 3 = 0 (3)
Ta có: △x = (y + 1)^2 – 4(y^2 + y + 3) = y^2 + 2y + 1 – 4y^2 – 4y – 12 = -(3y^2 + 2y + 11) (*)
Tính: Δy’ = 1 – 33 = -32 < 0. Suy ra pt (*) vô nghiệm.
Suy ra pt (3) vô nghiệm.
Vậy hệ phương trình có 2 nghiệm là: (– 1; – 1), (1;1).
Chọn đáp án B.
Câu 8: Hệ phương trình sau: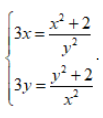 
. Khẳng định nào sau đây đúng?
A. Hệ phương trình vô nghiệm.
B. Hệ phương trình có 2 nghiệm.
C. Hệ phương trình có 1 nghiệm.
D. Hệ phương trình có 3 nghiệm
Lời giải:
Hướng dẫn:
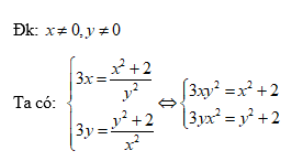
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Từ hệ phương trình ta thấy, x > 0, y > 0 ⇒ x + y + 3xy > 0. Vậy phương trình (3) vô nghiệm.
Vậy hệ phương trình có 1 nghiệm là: (1; 1).
Chọn đáp án C.
Câu 9: Hệ phương trình sau có bao nhiêu nghiệm: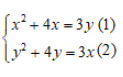 
A. 2
B. 3
C. vô số nghiệm
D. vô nghiệm
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Suy ra phương trình vô nghiệm
Vậy hệ phương trình có 4 nghiệm là: (0;0), (-1;-1)
Chọn đáp án A.
Câu 10: Hệ phương trình sau có bao nhiêu nghiệm: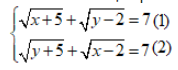 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Vì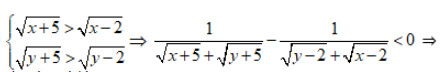 
phương trình vô nghiệm.
Vậy hệ phương trình có 1 nghiệm là: (11;11).
Chọn đáp án A.
THAM KHẢO THÊM:
