Mục lục bài viết
1. Hướng dẫn giải hệ phương trình đặc biệt nâng cao lớp 9:
Giải hệ phương trình bậc nhất hai ẩn
Để giải hệ phương trình bậc nhất hai ẩn, ta có thể tuân theo các bước sau:
– Sắp xếp các biến và hệ số trong hai phương trình theo dạng chuẩn: ax + by = c và dx + ey = f.
– Nhân phương trình thứ nhất với d và phương trình thứ hai với a. Khi đó, ta thu được hệ phương trình mới:
adx + bdy = cd
adx + aey = af
– Trừ phương trình thứ nhất từ phương trình thứ hai để loại bỏ biến x:
(aey – bdy) = af – cd
– Giải phương trình trên để tìm giá trị của y.
– Thay giá trị của y vào phương trình ban đầu để tìm giá trị của x.
– Kiểm tra lại kết quả bằng cách thay giá trị của x và y vào cả hai phương trình ban đầu.
Lưu ý: Trong trường hợp ae – bd = 0, tức là hệ số của y trong hai phương trình bằng nhau, thì hệ phương trình sẽ có vô số nghiệm hoặc không có nghiệm, tùy thuộc vào giá trị của af – cd.
Giải hệ phương trình bậc hai
Để giải hệ phương trình bậc hai, bạn có thể thực hiện các bước sau:
– Đưa hệ phương trình bậc hai về dạng tiêu chuẩn: ax² + bx + c = 0 và dx² + ex + f = 0.
– Tìm nghiệm của từng phương trình một để xác định giá trị của x:
+ Đối với phương trình ax² + bx + c = 0, sử dụng công thức nghiệm của phương trình bậc hai:
x₁ = (-b + √(b² – 4ac)) / (2a)
x₂ = (-b – √(b² – 4ac)) / (2a)
+ Đối với phương trình dx² + ex + f = 0, áp dụng công thức nghiệm của phương trình bậc hai tương tự.
– Để xác minh nghiệm, hãy thay giá trị x vào hệ phương trình gốc để kiểm tra xem chúng thực sự là nghiệm của hệ hay không.
Lưu ý: Trong quá trình giải phương trình bậc hai, bạn cần kiểm tra giá trị của delta (b² – 4ac) để xác định số lượng nghiệm. Nếu delta > 0, phương trình sẽ có hai nghiệm phân biệt. Nếu delta = 0, sẽ có một nghiệm kép, và nếu delta < 0, phương trình sẽ vô nghiệm.
Giải hệ phương trình bằng phương pháp thế
Cách tiến hành: Bắt đầu từ một phương trình trong hệ, chúng ta sẽ tách một biến ra khỏi phương trình đó và sau đó thay thế giá trị của biến này vào phương trình còn lại. Sau khi thực hiện việc giải phương trình còn lại (với chỉ còn một biến), chúng ta sẽ đưa kết quả này trở lại vào phương trình ban đầu.
– Chúng ta sử dụng quy tắc thế biến đổi hệ phương trình ban đầu thành một hệ mới với một phương trình chỉ còn một biến.
– Sau đó, chúng ta giải phương trình một biến này và dùng kết quả để suy ra nghiệm của hệ phương trình.
Giải hệ phương trình bằng phương pháp cộng đại số
Cách tiến hành: Chúng ta bắt đầu bằng việc làm cho các hệ số của biến x hoặc y trong cả hai phương trình trong hệ trở nên bằng nhau. Sau đó, chúng ta cộng hoặc trừ hai vế tương ứng của cả hai phương trình để thu được một phương trình mới. Chúng ta sẽ giải phương trình mới này để tìm ra giá trị của một biến, sau đó thay giá trị này vào một trong hai phương trình ban đầu để tìm biến còn lại.
– Chúng ta nhân cả hai vế của mỗi phương trình trong hệ với một hệ số thích hợp để làm cho giá trị tuyệt đối của hệ số của một biến nào đó trong cả hai phương trình trở nên bằng nhau.
– Bằng cách sử dụng quy tắc cộng đại số, chúng ta thu được một hệ phương trình mới với một phương trình chỉ còn một biến. Giải phương trình một biến này và sau đó sử dụng kết quả để suy ra nghiệm của hệ phương trình.
2. Bài tập vận dụng kèm hướng dẫn lời giải:
Bài 1: Giải các hệ phương trình sau bằng phương pháp thế:
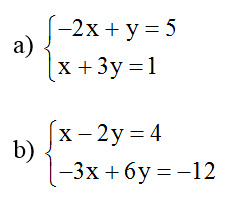
Hướng dẫn giải
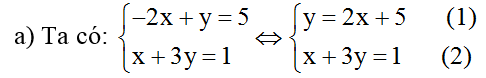
Thế (1) vào (2) ta được: x + 3(2x + 5) = 1
⇔ x + 6x + 15 = 1
⇔ 7x = -14
⇔ x = -2
Thay x = -2 vào (1) ta được y = 2.(-2) + 5 = 1
Vậy hệ phương trình có nghiệm duy nhất (-2;1)

Thế (1) vào (2) ta được: -3(2y + 4) + 6y = -12
⇔ -6y -12 + 6y = -12
⇔ 0y = 0 (luôn đúng)
Vậy hệ phương trình có vô số nghiệm (x;y) thỏa mãn x = 2y +4 và y ∈ R.
Bài 2: Cho hàm số y = ax + b. Xác định a, b để đồ thị hàm số đi qua hai điểm M(-1; 2) và N(√3;-7).
Hướng dẫn giải
Do hàm số y = ax + b có đồ thị đi qua M(-1; 2) nên thay x = -1 và y = 2 vào phương trình ta có: 2 = -a + b (1)
Tương tự, hàm số y = ax + b đi qua N(√3;-7) nên ta có: -7 = √3a + b (2)
Bài 3: Trong mặt phẳng Oxy, viết phương trình đường thẳng AB trong các trường hợp:
a) A(-1; 1) và B(2; 4)
b) A(0; -1) và B(1; 0)
Hướng dẫn giải
Gọi phương trình đường thẳng cần tìm là y=ax+b
Vì đường thẳng đi qua A(-1; 1) nên ta có: 1=-a+b (1)
Vì đường thẳng đi qua B(2;4) nên ta có: 4=2a+b (2)
Từ (1) và (2) => a = 3 và b = 4
Vậ
b, Gọi phương trình đường thẳng cần tìm là y = ax + b
Vì đường thẳng đi qua A(0;-1) nên ta có: -1 = 0.a + b ⇔ b = -1.
Vì đường thẳng đi qua B(1;0) nên ta có: 0 = a + b (1)
Thay b = -1 vào (1) ta được a = 1
Vậy đường thẳng cần tìm là y = x – 1.
Bài 4:
a) Giải hệ phương trình với m = -2.
b) Tìm m để hệ phương trình có nghiệm nguyên.
Hướng dẫn giải

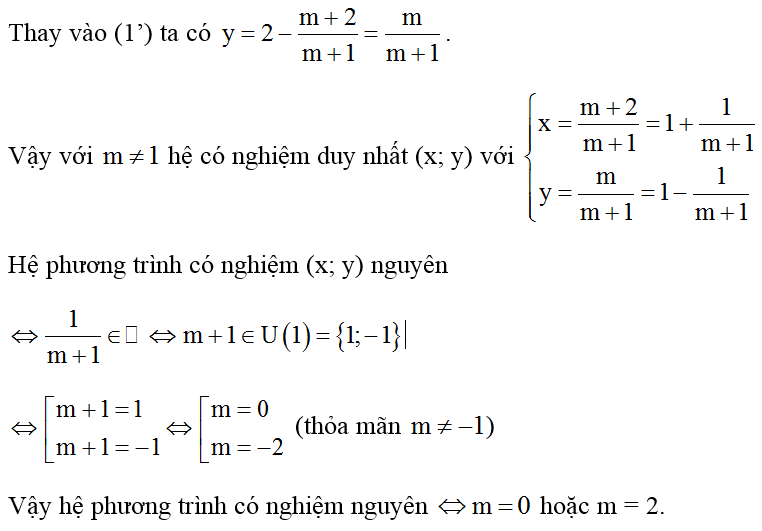
3. Nâng cao khả năng giải hệ phương trình ở lớp 9:
Giải hệ phương trình ở lớp 9 được xem là một phần kiến thức hữu ích và quan trọng trong môn Đại số. Đây là nội dung giúp học sinh hiểu cách giải quyết các loại toán liên quan đến hệ phương trình bậc nhất và bậc hai với hai ẩn số. Để cải thiện khả năng giải hệ phương trình ở lớp 9, có một loạt các bước mà bạn có thể tuân theo để đảm bảo bạn hiểu và ứng dụng kiến thức một cách thành thạo:
– Xây dựng kiến thức cơ bản về đại số và phương trình: Trước khi bắt đầu giải hệ phương trình, điều quan trọng là bạn phải xây dựng một nền tảng vững chắc về đại số và phương trình. Hiểu rõ về biến số, hệ số và cách thức hoạt động của phương trình là bước đầu tiên quan trọng.
– Hiểu rõ các phương pháp giải hệ phương trình: Hệ phương trình có nhiều phương pháp giải khác nhau, chẳng hạn như phương pháp cộng trừ, phương pháp thế, phương pháp khử, và phương pháp đại số đối xứng. Hiểu cách áp dụng mỗi phương pháp này để giải các dạng bài tập khác nhau là một phần quan trọng của quá trình học.
– Luyện tập với nhiều dạng bài tập: Để trở nên thành thạo trong việc giải hệ phương trình, bạn cần thực hành giải nhiều bài tập khác nhau. Bắt đầu từ các bài tập dễ và dần chuyển đến các bài tập phức tạp hơn sẽ giúp bạn phát triển khả năng giải quyết các vấn đề đa dạng.
– Ôn tập và làm bài tập thường xuyên: Để duy trì và củng cố kiến thức, việc ôn tập và làm bài tập thường xuyên là quan trọng. Không chỉ giúp bạn nắm vững kiến thức mà còn giúp bạn thấy thoải mái khi tiếp cận với các bài tập mới.
– Tìm nguồn tài liệu học tập đầy đủ: Cố gắng tìm kiếm các tài liệu học tập về giải hệ phương trình trên internet hoặc sử dụng sách giáo khoa của trường để nắm vững kiến thức. Các nguồn tài liệu này thường cung cấp ví dụ và bài tập bổ sung để bạn luyện tập. Khả năng giải hệ phương trình cần sự kiên nhẫn và thời gian để phát triển. Bằng việc tuân theo các bước trên và không ngừng rèn luyện, bạn sẽ nâng cao kỹ năng giải hệ phương trình một cách hiệu quả.
THAM KHẢO THÊM:




