Hệ phương trình bậc nhất 3 ẩn là dạng kiến thức quan trọng trong chương trình toán học phổ thông và thường xuyên xuất hiện trong các bài thi và kiểm tra cuối kỳ. Sau đây là Giải Toán Ứng dụng của hệ phương trình bậc nhất ba ẩn chi tiết và các kiến thức liên quan, mời các bạn cùng tham khảo!
Mục lục bài viết
1. Câu hỏi giữa bài chuyên đề toán 10:
Hoạt động 1 trang 15 Chuyên đề Toán 10:
Bài toán sản xuất gà giống. Trong trang trại sản xuất gà giống, việc lựa chọn tỉ lệ giữa gà trống và gà mái rất quan trọng. Nếu quá nhiều gà trống thì không hiệu quả kinh tế, nếu ít gà trống quá thì ảnh hưởng đến hiệu quả sản xuất gà giống. Các nghiên cứu chỉ ra rằng tỉ lệ giữa gà trống và gà mái để sản xuất gà giống hiệu quả nhất là 1:10,5. Một đàn gà trường thành có tồng số 3 000 con, trong đó tỉ lệ giữa gà trống và gà mái là 5:3. Cần chuyền bao nhiêu gà trống cho mục đích nuôi lấy thịt để hiệu quả cao nhất?
Gọi số gà trống trong đàn gà là x, số gà mái trong đàn gà là y, số gà trống cần chuyển sang mục đích nuôi lấy thịt là z.
a) Điều kiện của x, y và z là gì?
b) Từ giả thiết của bài toán, hãy tìm ba phương trình bậc nhất ràng buộc x, y và z, từ đó có một hệ phương trình bậc nhất ba ẩn.
c) Giải hệ phương trình bậc nhất thu được. Từ đó đưa ra câu trả lời cho bài toán.
Lời giải:
a) Điều kiện của x, y và z là x, y, z là các số tự nhiên nhỏ hơn 3000.
b) Từ giả thiết của bài toán, ta có:
x + y = 3000 (1)
x : y = 5 : 3 hay 5x = 3y hay 5x – 3y = 0 (2)
(x – z) : y = 1 : 10,5 hay x – z = 10,5y hay x – 10,5y – z = 0 (3)
Vậy ta có hệ phương trình:
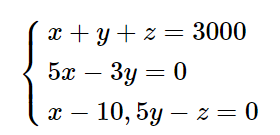
c) Giải hệ phương trình thu được ở câu b) ta được x = SAI ĐỀ!
2. Câu hỏi chuyên đề cung – cầu:
Hoạt động 2 trang 18 Chuyên đề Toán 10:
Kí hiệu x, y, z lần lượt là giá của 1 kg thịt lợn, 1 kg thịt bò và 1 kg thịt gà, ở đây x, y, z > 0 và đơn vị là nghìn đồng. Kí hiệu:
QS1 là lượng thịt lợn mà người bán chấp thuận bán với giá x.
QS2 là lượng thịt bò mà người bán chấp thuận bán với giá y.
QS3 là lượng thịt gà mà người bán chấp thuận bán với giá z.
QD1 là lượng thịt lợn mà người mua chấp thuận mua với giá x.
QD2 là lượng thịt bò mà người mua chấp thuận mua với giá y.
QD3 là lượng thịt gà mà người mua chấp thuận mua với giá z.
a) Mức giá thịt lợn x, thịt bò y và thịt gà z phải thoả mãn điều kiện gì để người bán và người mua cùng hài lòng, tức là mức giá hợp lí nhất?
b) Viết hệ phương trình ràng buộc giữa x, y, z để người bán và người mua cùng hài lòng.
Trong kinh tế học người ta gọi :
– Các hàm QS1, QS2 và QS3 phụ thuộc vào ba biến giá x, y, z là hàm cung (supply function);
– Các hàm QD1, QD2 và QD3 phụ thuộc vào ba biến giá x, y, z là hàm cầu (demand function);
– Hệ phương trình QS1=QD1QS2=QD2QS3=QD3″> gọi là hệ phương trình cân bằng cung – cầu.
Lời giải:
a) Mức giá thịt lợn x, thịt bò y và thịt gà z phải thoả mãn các điều kiện:
– Lượng thịt lợn mà người bán chấp thuận bán với giá x bằng lượng thịt lợn mà người mua chấp thuận mua với giá x.
– Lượng thịt bò mà người bán chấp thuận bán với giá y bằng lượng thịt bò mà người mua chấp thuận mua với giá y.
– Lượng thịt gà mà người bán chấp thuận bán với giá z bằng lượng thịt gà mà người mua chấp thuận mua với giá z.
b) Hệ phương trình ràng buộc giữa x, y, z để người bán và người mua cùng hài lòng: 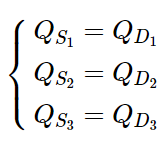
3. Bài tập kèm lời giải:
Bài 1.8 trang 20 Chuyên đề Toán 10: Em Hà so sánh tuổi của mình với chị Mai và anh Nam. Tuổi của anh Nam gấp ba lần tuổi của em Hà. Cách đây bảy năm tuổi của chị Mai bằng nửa số tuổi của anh Nam. Ba năm nữa tuổi của anh Nam bằng tổng số tuổi của chị Mai và em Hà. Hỏi tuổi của mỗi người là bao nhiêu?
Lời giải:
Gọi tuổi hiện nay của em Hà, chị Mai, anh Nam lần lượt là x, y, z.
Theo đề bài ta có:
– Tuổi của anh Nam gấp ba lần tuổi của em Hà, suy ra z = 3x hay 3x – z = 0 (1).
– Cách đây bảy năm tuổi của chị Mai bằng nửa số tuổi của anh Nam, suy ra (y – 7) = 1212(z – 7) hay 2y – z = 7 (2).
– Ba năm nữa tuổi của anh Nam bằng tổng số tuổi của chị Mai và em Hà, suy ra (z + 3) = (x + 3) + (y + 3) hay x + y – z = –3 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
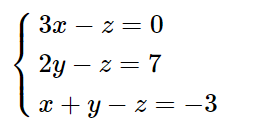
Giải hệ này ta được x = 13, y = 23, z = 39.
Vậy tuổi hiện nay của em Hà, chị Mai, anh Nam lần lượt là 13, 23, 39.
Bài 1.9 trang 20 Chuyên đề Toán 10: Bác Việt có 330740 nghìn đồng, bác chia số tiền này thành ba phần và đem đầu tư vào ba hình thức : Phần thứ nhất bác đầu tư vào chứng khoán với lãi thu được 4% một năm; phần thứ hai bác mua vàng thu lãi 5% một năm và phần thứ ba bác gửi tiết kiệm với lăii suất 6% một năm. Sau một năm, kể cả gốc và lãi bác thu được ba món tiền bằng nhau. Hỏi tổng số tiền cả gốc và lãi bác thu được sau một năm là bao nhiêu?
Lời giải:
Gọi số tiền bác Việt đầu tư vào chứng khoán, mua vàng, gửi tiết kiệm lần lượt là x, y, z (nghìn đồng).
Theo đề bài ta có:
– Tổng số tiền là 330740 nghìn đồng, suy ra x + y + z = 330740 (1).
– Số tiền kể cả gốc lẫn lãi bác Việt thu được từ ba khoản là x + 4%x, y + 5%y, z + 6%z. Vì bác thu được ba món tiền bằng nhau nên x + 4%x = y + 5%y = z + 6%z
⇒ 104%x = 105%y = 106%z
⇒ 104x – 105y = 0 (2) và 105y – 106z = 0 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
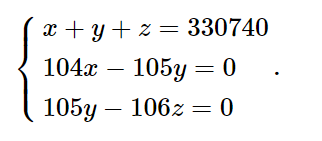
Giải hệ này ta được x = 111300, y = 110240, z = 109200.
Vậy số tiền bác Việt đầu tư vào chứng khoán, mua vàng, gửi tiết kiệm lần lượt là 111300 nghìn đồng, 110240 nghìn đồng, 109200 nghìn đồng.
Bài 1.10 trang 20 Chuyên đề Toán 10: Một tuyến cáp treo có ba loại vé sau đây: vé đi lên giá 250 nghìn đồng; vé đi xuống giá 200 nghìn đồng và vé hai chiều giá 400 nghìn đồng. Một ngày nhà ga cáp treo thu được tổng số tiền là 251 triệu đồng. Tìm số vé bán ra mỗi loại, biết rằng nhân viên quản lí cáp treo đếm được 680 lượt người đi lên và 520 lượt người đi xuống.
Lời giải:
Gọi số vé bán ra loại đi lên, đi xuống và hai chiều lần lượt là x, y, z.
Theo đề bài ta có:
– Nhà ga cáp treo thu được tổng số tiền là 251 triệu đồng, suy ra 250000x + 200000y + 400000z = 251000000 hay 250x + 200y + 400z = 251000 (1).
– Có 680 lượt người đi lên, suy ra x + z = 680 (2).
– Có 520 lượt người đi xuống, suy ra y + z = 520 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
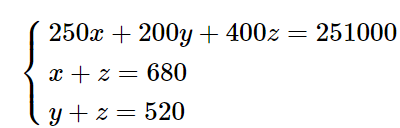
Giải hệ này ta được x = 220, y = 40, z = 460.
Vậy số vé bán ra loại đi lên, đi xuống và hai chiều lần lượt là 220, 60, 460.
Bài 1.11 trang 20 Chuyên đề Toán 10: Ba lớp 10A, 10B, 10C của một trường trung học phồ thông gồm 128 em cùng tham gia lao động trồng cây. Tính trung bình, mỗi em lớp 10A trồng được 3 cây xoan và 4 cây bạch đàn; mỗi em lớp 10B trồng được 2 cây xoan và 5 cây bạch đàn; mối em lớp 10 C trồng được 6 cây xoan. Cả ba lớp trồng được tổng cộng 476 cây xoan và 375 cây bạch đàn. Hỏi mỗi lớp có bao nhiêu em?
Lời giải:
Gọi số học sinh ba lớp 10A, 10B, 10C lần lượt là x, y, z.
Theo đề bài ta có:
– Ba lớp có 128 học sinh, suy ra x + y + z = 128 (1).
– Cả ba lớp trồng được tổng cộng 476 cây xoan, suy ra 3x + 2y + 6z = 476 (2).
Cả ba lớp trồng được tổng cộng 375 cây bạch đàn, suy ra 4x + 5y = 375 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
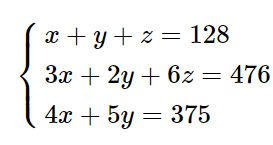
Giải hệ này ta được x = 40, y = 43, z = 45.
Vậy số học sinh ba lớp 10A, 10B, 10C lần lượt là 40, 43, 45 học sinh.
THAM KHẢO THÊM:




