Mục lục bài viết
1. Lý thuyết giải hệ phương trình bằng phương pháp thế Toán 9 Bài 3:
1.1. Một số lý thuyết về cách giải hệ phương trình bằng phương pháp thế:
– Nói chung muốn giải một hệ phương trình hai ẩn, ta tìm cách biến đổi hệ phương trình đã cho để được một hệ phương trình mới tương đương, trong đó một phương trình của nó chỉ còn một ẩn. Một trong các cách giải là áp dụng quy tắc sau gọi là quy tắc thế.
– Quy tắc thế là dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương. Quy tắc thế gồm hai bước được tóm tắt như sau:
+ Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn)
+ Bước 2: Dùng phương trình mới ấy để thay thế cho phương trình thứ hai trong hệ (phương trình thứ nhất cũng thường được thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia có được ở bước 1).
Ví dụ 1:Xét hệ phương trình: Xét hệ phương trình
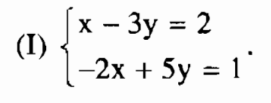
Việc áp dụng quy tắc thế đối với hệ (I) như sau:
Bước 1: Từ phương trình thứ nhất, biểu diễn x theo y ta có: x = 3y +2 (*).
Lấy kết quả này thế vào chỗ của x trong phương trình thứ hai thì ta được:
-2(3y+2) + 5y = 1
Bước 2: Dùng phương trình vừa có, thay thế cho phương trình thứ hai của hệ và dùng (*) thay thế cho phương trình thứ nhất, ta được hệ phương trình:
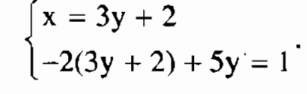
Vậy hệ (I) có nghiệm duy nhất là (-13, -5).
Sau khi đã áp dụng quy tắc thế, ta thấy ngay có thể giải hệ (I) như sau:
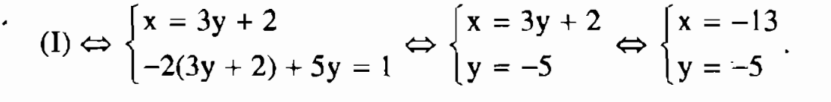
Cách giải hệ như trên gọi là giải hệ phương trình bằng phương pháp thế.
– Chú ý: Nếu trong quá trình giải hệ phương trình bằng phương pháp thế, ta thấy xuất hiện phương trình có các hệ số của cả hai ẩn đều bằng 0 thì hệ phương trình đã cho có thể có vô số nghiệm hoặc vô nghiệm.
– Ví dụ số 2: giải hệ phương trình sau:
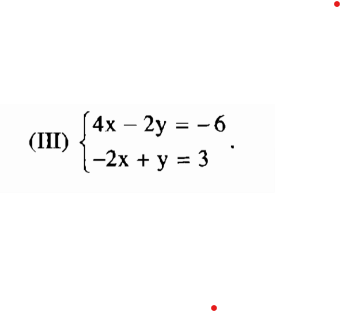
Lời giải minh họa:
+ Biểu diễn y theo x từ phương trình thứ hai, ta được: y = 2x+3.
+ Thế y trong phương trình đầu bởi 2x + 3, ta có:
4x – 2(2x+3) = -6 ó 0x = 0
Vậ
– Tóm tắt cách giửi hệ phương trình bằng phương pháp thế:
+ Dùng quy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới, trong đó có một phương trình một ẩn.
+ Ta giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ đã cho.
– Một số lưu ý khi giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế:
+ Trước khi cộng các vế của hai phương trình trong hệ lại với nhau, ta có thể nhân hai vế của mỗi phương trình đó với một số thích hợp (nếu cần)
+ Nếu hệ số của hai ẩn trong hệ đều bằng 0 thì hệ phương trình đó có thể vô nghiệm hoặc có vô số nghiệm.
+ Bên cạnh hai phương pháp trên, ta có thể dùng quy tắc đặt ẩn phụ
+ Tùy vào các dữ kiện đề bài và kiến thức của bản thân để chọn cách giải phù hợp.
– Để giải hệ phương trình bằng phương pháp thế, ta cần thực hiện các bước sau:
Bước 1: Xác định số lượng phương trình và số lượng ẩn trong hệ phương trình.
Bước 2: Chọn một phương trình trong hệ làm phương trình tiêu biểu. Phương trình tiêu biểu thường được chọn dựa trên độ phức tạp của phép tính hoặc sự thích hợp với từng trường hợp cụ thể.
Bước 3: Giải phương trình tiêu biểu để tìm ra giá trị của một ẩn (giả sử là x) dựa trên các ẩn khác trong phương trình. Sau đó, thay thế giá trị này vào các phương trình khác trong hệ.
Bước 4: Lặp lại bước 3 cho các ẩn còn lại trong hệ, cho đến khi tìm được giá trị của tất cả các ẩn.
Bước 5: Kiểm tra lại giá trị của các ẩn bằng cách thay thế vào tất cả các phương trình trong hệ, đảm bảo tất cả các phương trình đều vẫn đúng. Nếu có phương trình nào không đúng, có thể xảy ra lỗi trong quá trình giải.
Bước 6: Viết lại kết quả cuối cùng, gồm giá trị của tất cả các ẩn, và kiểm tra lại kết quả với bộ đề bài ban đầu.
1.2. Hướng dẫn giải các câu hỏi trong phần lý thuyết:
Câu hỏi số 1: giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ):
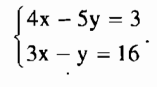
Bước 1: Từ phương trình thứ 2, biểu diễn y theo x, ta có: y = 3x – 16 (*). Lấy kết quả này thế vào chỗ của y ở phương trình thứ nhất thì ta được:
4x – 5(3x – 16) = 3.
Bước 2: Dùng phương trình vừa có, thay thế cho phương trình thứ nhất của hệ và dùng (*) thay thế cho phương trình phương trình thứ hai, ta được hệ phương trình:
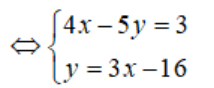
Sau khi đã áp dụng quy tắc thế, ta thấy ngay có thể giải hệ như sau:
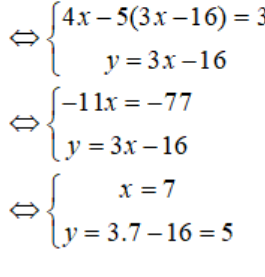
Vậy hệ phương trình đã cho có nghiệm duy nhẩ là (7;5).
Câu hỏi số 2: Bằng minh họa hình học, hãy giải thích tại sao hệ (III) có vô số nghiệm:
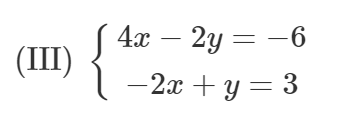
Lời giải minh họa cho câu hỏi số 2:
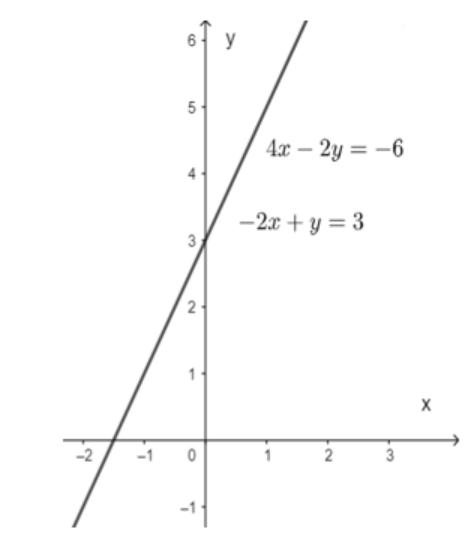
Hai đường thẳng trên trùng nhau nên hệ phương trình (III) có vô số nghiệm
Câu hỏi số 3: Bằng minh họa hình học và bằng phương pháp thế, chứng tỏ hệ (IV) vô nghiệm:
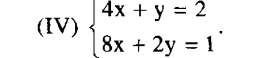
– Bằng phương pháp minh họa hình học:
+ Chuyển đổi hai phương trình bậc nhất hai ẩn về dạng y= ax+b.
+ Sau đó, vẽ phương trình hai đường thẳng đó. Nếu hai đường cắt nhau thì hệ đã cho có 1 nghiệm duy nhất, hai đường thẳng trùng nhau thì hệ phương trình đã cho có vô số nghiệm, nếu hai đường thẳng song song với nhau thì hệ đã cho vô nghiệm.
Hai đường thẳng trên song song với nhau nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm
* Bằng phương pháp thế:
+ Bước 1: Từ phương trình thứ nhất, biểu diễn y theo x, ta có: y = -4x +2 (*). Lấy kết quả này thế vào chỗ của y ở phương trình thứ hai thì ta được:
8x +2(-4x+2) = 1
+ Bước 2: Dùng phương trình vừa có, thay thế cho phương trình thứ nhất của hệ và dùng (*) thay thế cho phương trình phương trình thứ hai, ta được hệ phương trình:
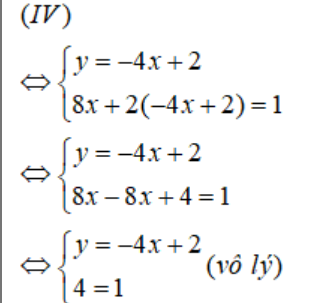
Vậy hệ phương trình (IV) vô nghiệm.
2. Hướng dẫn phần bài tập giải hệ phương trình bằng phương pháp thế Toán 9 Bài 3 tập 2:
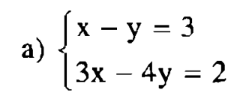
2.1. Câu hỏi số 12 trang 15 Toán 9 Bài 3 tập 2:
– Bước 1: Từ phương trình thứ nhất, biểu diễn x theo y, ta có x = y + 3 (*).
Lấy kết quả này thế vào chỗ của x trong phương trình thứ hai ta được:
3(y+3) – 4y = 2
– Bước 2: Từ hệ phương trình vừa có, thay thế cho phương trình thứ hai của hệ và dùng (*) thay thế cho phương trình thứ nhất, ta được hệ phương trình:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7..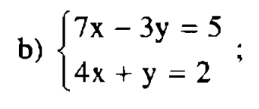
– Bước 1: Từ phương trình thứ hai, biểu diễn y theo x, ta có y = 4x – 2 (*).
Lấy kết quả này thế vào chỗ của x trong phương trình thứ nhất ta được:
7x – 3(4x-2) = 5
– Bước 2: Dùng phương trình vừa có, thay thế cho phương trình thứ nhất của hệ và dùng (*) thay thế cho phương trình thứ hai, ta được hệ phương trình:
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 <=> x = 11/9.
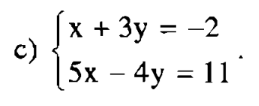
– Bước 1: Từ phương trình thứ nhất, biểu diễn x theo y, ta có x = -3y – 2 (*).
Lấy kết quả này thế vào chỗ của x trong phương trình thứ hai ta được:
5x – 4(-3y-2) = 11
– Bước 2: Dùng phương trình vừa có, thay thế cho phương trình thứ hai của hệ và dùng (*) thay thế cho phương trình thứ nhất, ta được hệ phương trình:
Thế x = -3y – 2 vào phương trình (2) ta được :
5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21.
2.2. Câu hỏi số 13 trang 15 Toán 9 Bài 3 tập 2:
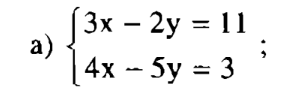
– Bước 1: Từ phương trình thứ nhất, biểu diễn y theo x, ta có y = (3x – 11)/2 (*).
Lấy kết quả này thế vào chỗ của x trong phương trình thứ hai ta được:
4x – 5(3x-11)/2 = 3
– Bước 2: Dùng phương trình vừa có, thay thế cho phương trình thứ hai của hệ và dùng (*) thay thế cho phương trình thứ nhất, ta được hệ phương trình:
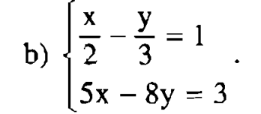
– Bước 1: Từ phương trình thứ hai, biểu diễn x theo y, ta có x = (8y +3)/5 (*).
Lấy kết quả này thế vào chỗ của x trong phương trình thứ nhất ta được:
(8y+3)/10 – y/3 = 1
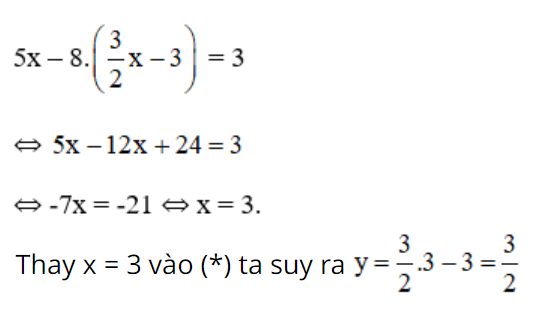
– Bước 2: Dùng phương trình vừa có, thay thế cho phương trình thứ hai của hệ và dùng (*) thay thế cho phương trình thứ nhất, ta được hệ phương trình:
2.3. Câu hỏi số 14 trang 15 Toán 9 Bài 3 tập 2:

Vậy đã cho có nghiệm duy nhất là : 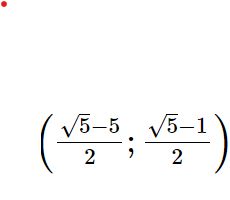
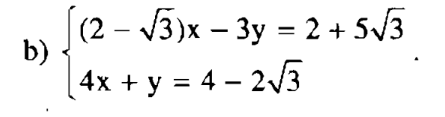
Từ (2) ta rút ra được y = -4x + 4 – 2 căn 3 (*)
Thế (*) vào phương trình (1) ta được:

3. Một số bài tập thêm về giải hệ phương trình bằng phương pháp thế Toán 9:
Bạn hãy giải hệ phương trình sau trong mỗi trường hợp:
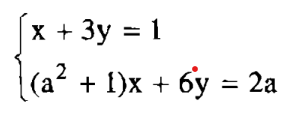
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được :
(a2 + 1).(1 – 3y) + 6y = 2a
⇔ a2 + 1 – 3(a2 + 1)y + 6y = 2a
⇔ a2 +1- 2a = 3a2.y – 6y + 3y
⇔ ( a- 1)2 = 3a2y – 3y
⇔ 3(a2 – 1).y = (a – 1)2 (**)
+ a= -1 thì phương trình (**) trở thành : 0y = 4
Phương trình trên vô nghiệm
Vậy hệ phương trình khi a = -1 vô nghiệm.
+ a = 1, phương trình (**) trở thành: 0y = 0
Phương trình nghiệm đúng với mọi y.
Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1-3y, y) (y thuộc R).
THAM KHẢO THÊM:




