Đường tròn nội tiếp tam giác là gì? Nêu cách xác định?

1. Đường tròn nội tiếp tam giác là gì?

Khái niệm về đường tròn và đường tròn nội tiếp tam giác không chỉ là những khái niệm cơ bản trong hình học mà còn là nền tảng cho nhiều bài toán trong toán học. Để hiểu rõ hơn về chúng, hãy đi vào chi tiết.

Đầu tiên, đường tròn là một tập hợp của tất cả các điểm trên một mặt phẳng sao cho khoảng cách từ mỗi điểm đến một điểm cố định được gọi là tâm của đường tròn bằng một giá trị cố định, gọi là bán kính. Trong đó, điểm được chọn làm tâm của đường tròn được gọi là O và khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn được gọi là bán kính, thường được ký hiệu là r. Tóm lại, một đường tròn có thể được biểu diễn bằng cặp (O; r).

Một khái niệm quan trọng khác là đường tròn nội tiếp tam giác. Đường tròn nội tiếp tam giác là một đường tròn tiếp xúc với các cạnh của một tam giác hoặc nói cách khác là đường tròn nội tiếp tam giác cũng được gọi là tam giác ngoại tiếp đường tròn.

Khi nói về đường tròn nội tiếp tam giác, chúng ta liên tưởng ngay đến hình ảnh của một đường tròn tiếp xúc với các cạnh của một tam giác. Điều này có nghĩa là đường tròn này chạm vào các cạnh của tam giác từ bên trong, tạo ra một liên kết mạnh mẽ giữa các thành phần hình học trong bài toán. Đường tròn nội tiếp tam giác cung cấp một cách tiếp cận hiệu quả để xác định các đặc tính của tam giác thông qua các thuộc tính của đường tròn và ngược lại.

Trong toán học, việc nắm vững các khái niệm này không chỉ giúp chúng ta hiểu rõ hơn về cơ bản của hình học mà còn mở ra cánh cửa cho nhiều ứng dụng và bài toán phức tạp hơn trong tương lai.

Tính chất của đường tròn nội tiếp tam giác

Tính chất của đường tròn nội tiếp tam giác là một khía cạnh quan trọng và thú vị trong hình học, với nhiều đặc điểm đáng chú ý:

– Mỗi tam giác chỉ có duy nhất 1 đường tròn nội tiếp:

Điều này có nghĩa là cho mỗi tam giác, chỉ có một đường tròn có thể được vẽ sao cho nó tiếp xúc với tất cả các cạnh của tam giác đó. Điều này có thể được chứng minh bằng cách sử dụng tính chất của các góc và các cạnh của tam giác, cùng với tính chất của đường tròn và đường thẳng.

– Bán kính của đường tròn nội tiếp tam giác chính bằng khoảng cách từ tâm hạ vuông góc xuống ba cạnh của tam giác:

Bán kính của đường tròn nội tiếp tam giác là một khía cạnh đặc biệt. Nó chính bằng với khoảng cách từ tâm của đường tròn đến điểm tiếp xúc của đường tròn với một trong các cạnh của tam giác và điểm tiếp xúc này thường nằm ở trung điểm của cạnh tương ứng.

– Trong tam giác đều, tâm đường tròn nội tiếp và đường tròn ngoại tiếp trùng nhau:

Đây là một điểm đặc biệt và đáng chú ý. Trong một tam giác đều, tâm của đường tròn nội tiếp và tâm của đường tròn ngoại tiếp là cùng một điểm. Điều này tạo ra một sự liên kết đặc biệt giữa các khái niệm này và tạo ra một sự tương quan độc đáo trong hình học tam giác.

Những tính chất này không chỉ là các định lý quan trọng trong hình học mà còn có ứng dụng rộng rãi trong giải các bài toán và ứng dụng thực tế. Việc hiểu rõ và áp dụng chúng giúp ta khám phá và thú vị hơn trong việc nghiên cứu về hình học và toán học.

2. Cách xác định Đường tròn nội tiếp tam giác:

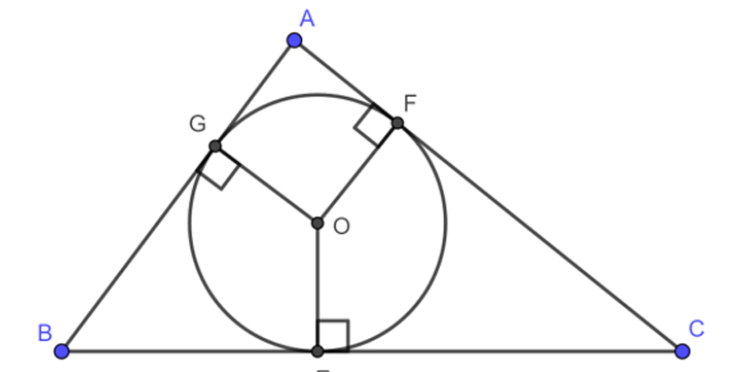
Để xác định tâm của đường tròn nội tiếp tam giác, ta cần thực hiện một loạt các bước cụ thể và chính xác. Dưới đây là phương pháp chi tiết để thực hiện điều này:

– Bước 1: Vẽ tam giác và các cạnh của nó

Bắt đầu bằng việc vẽ tam giác và đảm bảo rằng các đỉnh và cạnh của tam giác được xác định chính xác trên mặt phẳng.

– Bước 2: Xác định các giao điểm của các đường phân giác tam giác

Đường phân giác của một góc trong tam giác là đường thẳng đi qua gốc của góc đó và chia góc thành hai phần bằng nhau. Để xác định các giao điểm của các đường phân giác, ta vẽ các đường này từ mỗi góc của tam giác và chia mỗi góc thành hai phần bằng nhau, sau đó xác định điểm giao điểm của chúng.

– Bước 3: Kẻ đường thẳng nối các giao điểm của các đường phân giác

Sau khi đã xác định các điểm giao điểm của các đường phân giác, ta kết nối chúng bằng các đoạn thẳng để tạo thành một đường thẳng mới. Đường thẳng này sẽ chứa tâm của đường tròn nội tiếp tam giác.

– Bước 4: Xác định tâm đường tròn nội tiếp tam giác

Tâm của đường tròn nội tiếp tam giác chính là điểm giao điểm của các đường phân giác. Điều này có nghĩa là tâm của đường tròn nội tiếp sẽ là điểm mà các đường phân giác gặp nhau.

Lưu ý:

Trong trường hợp tam giác không đều, các đường phân giác của các góc trong tam giác có thể không gặp nhau tại cùng một điểm, do đó không thể áp dụng phương pháp trên để xác định tâm của đường tròn nội tiếp. Trong trường hợp này, ta cần sử dụng các phương pháp khác, như sử dụng trung điểm của các cạnh hoặc tính toán trên các đỉnh và góc của tam giác để tìm ra tâm của đường tròn nội tiếp.

– Các trường hợp đặc biệt

Có một số trường hợp đặc biệt trong việc xác định đường tròn nội tiếp tam giác:

+ Tam giác vuông: Trong trường hợp này, đường tròn nội tiếp sẽ đi qua đỉnh vuông và điểm chính giữa của cạnh huyền.

+ Tam giác cân: Trong tam giác cân, đường tròn nội tiếp sẽ đi qua trung điểm của cạnh đáy và giao điểm của các đường phân giác.

+ Tam giác đều: Trong tam giác đều, tâm của đường tròn nội tiếp trùng với tâm của tam giác và bán kính của đường tròn là một phần của độ dài cạnh.

Việc này không chỉ giúp ta hiểu rõ về cấu trúc và tính chất của tam giác mà còn có thể ứng dụng trong giải các bài toán hình học phức tạp.

3. Bài tập liên quan kèm lời giải:

Bài 1

a) Vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).

Vẽ hình minh họa

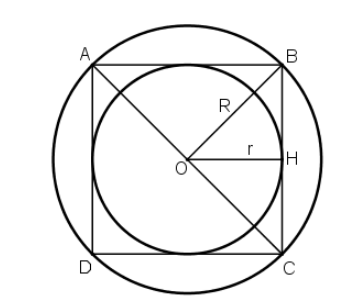
a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.

b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).

c) Vẽ OH ⊥ BC.

⇒ OH là khoảng cách từ từ tâm O đến BC

Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)

⇒ O là tâm đường tròn nội tiếp hình vuông ABCD

OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.

Tam giác vuông OBC có OH là đường trung tuyến ⇒ OH = 1/2 BC=BH

Xét tam giác vuông OHB có: r2 + r2 = OB2 = 22 ⇒ 2r2 = 4 ⇒ r2 = 2 ⇒ r = √2(cm)

Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

Bài 2

a) Vẽ tam giác đều ABC cạnh a = 3cm.

b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.

c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.

d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).

GIẢI

Vẽ hình

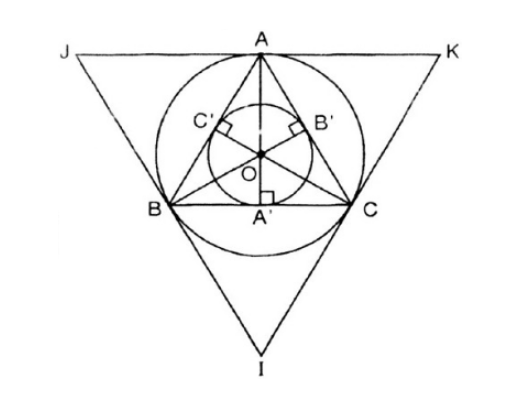
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa).

+ Dựng đoạn thẳng AB = 3cm .

+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b) Gọi A’;B’;C’ lần lượt là trung điểm của BC;AC;AB.

Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác AA’;BB’;CC’ của tam giác đều ABC).

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực cắt nhau tại O.

Vẽ đường tròn tâm O, bán kính R=OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.

Tính AA’:

GIẢI

Xét tam giác AA’C vuông tại A’ có AC=3;A’C=3/2, theo định lý Pytago ta có

AC^2=AA’^2+A’C^2 =>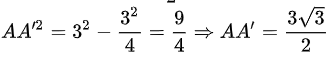

Theo cách dựng ta có O cũng là trọng tâm tam giác ABC nên OA=2/3AA’

Ta có bán kính đường tròn ngoại tiếp tam giác ABC là R= OA = 2/3AA’ = .

c) Do tam giác ABC là tam giác đều các trung điểm A’; B’; C’ của các cạnh BC; CA; AB đồng thời là chân đường phân giác hạ từ A, B, C đến BC, AC, AB.

Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A’, B’, C’ của các cạnh.

Hay đường tròn (O; r) là đường tròn tâm O; bán kính r=OA’ = OB’ = OC’.

Ta có:

d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).