Khái niệm hình tròn là kiến thức trọng tâm của Toán học lớp 3, phần kiến thức rất hay có trong các đề thi giữa kì hay cuối kì của các em. Vậy cụ thể hình tròn là gì, đường kinh là gì, bán kinh là gì, tâm đường tròn như nào?… Bài viết dưới đây của chúng minh sẽ giúp bạn giải đáp nhé!
Mục lục bài viết
1. Giới thiệu hình tròn?
Trong cuộc sống của chúng ta thì hình tròn là một hình rất là phổ biến nó xuất hiện ở khắp mọi nơi từ các vật dụng con người sử dụng hàng ngày cho đến các công trình mang tầm kiến trúc hiện đại,… Tuy nhiên, hầu hết chúng ta chỉ tiếp xúc đến hình tròn qua quan sát bằng mắt thường chứ chưa tìm hiểu và hiểu một cách cặn kẽ theo chiều hướng toán học. Vậy nếu trong toán học thì hình tròn sẽ được thể hiện như thế nào?
Hình tròn là một vùng trên mặt phẳng nằm bên trong đường tròn. Tâm, bán kính và chu vi của hình tròn chính là tâm và bán kính của đường tròn bao quanh nó.
Đường tròn là đường bao quanh hình tròn. Đường tròn hay còn gọi là chu vi của hình tròn. Đường tròn không có diện tích. Điểm nằm ở chính giữa của đường tròn chính là Tâm của đường tròn đó.
Đường kính của hình tròn là đoạn thẳng nối hai điểm bất kỳ trên đường tròn và đi qua tâm đường tròn đó.
Bán kính hình tròn chính là đoạn thẳng đi qua tâm và cắt đường tròn tại một điểm có nửa đường kính.
Một số Ví dụ về hình tròn: Mặt đồng hồ hình tròn, mặt đĩa hình tròn, thớt hình tròn, miệng bát hình tròn, miệng chậu hình tròn…
Từ đó ta rút ra nhận xét: Trong một hình tròn: Tâm O chính là trung điểm của đường kính AB. Độ dài của đường kính sẽ gấp hai lần độ dài của bán kinh. Hình tròn có một tâm và vô số bán kính và đường kính.
Vậy cách để vẽ một hình tròn sẽ theo các bước sau đây:
Để vẽ một hình tròn bán kính 2cm:
Bước 1: Chúng ta mở rộng compa và đo trên thước kẻ với khoảng cách là 2 cm
Bước 2: Đánh dấu tâm O của hình tròn
Bước 3: Đặt đầu có đỉnh nhọn của compa vào đúng tâm O, quay đầu bút chì một vòng theo chiều kim đồng hồ
2. Định nghĩa hình tròn:
Như chúng ta đã biết trong hình học, hình tròn là một diện tích trong mặt phẳng giới hạn bởi một đường tròn. Một đường tròn được gọi là đóng nếu nó chứa đường tròn tạo thành ranh giới của nó và mở nếu ngược lại. Hay theo một cách định nghĩa khác: Hình tròn là hình gồm các điểm nằm trên và nằm trong đường tròn.
Tâm, bán kính và chu vi của một hình tròn là tâm và bán kính của chính đường tròn bao quanh nó.
Như vậy, hình tròn là một diện tích trên mặt phẳng nằm bên trong đường tròn. Tâm, bán kính và chu vi của một hình tròn là tâm và bán kính của đường tròn bao quanh nó. Một hình tròn được gọi là đóng hoặc mở tùy theo công việc mà nó chứa hoặc không chứa đường trơn biên.
Định nghĩa đường tròn là gì?
Trong hình học phẳng, đường tròn (hay vòng tròn) là tập hợp tất cả các điểm trên một mặt phẳng, cách đều một điểm cho trước một khoảng nào đó. Điểm trước đó được gọi là tâm của đường tròn và khoảng đã cho được gọi là bán kính của đường tròn.
Đường tròn tâm O bán kính R được kí hiệu là (O; R).
Đường tròn là một hình khép kín đơn giản chia mặt phẳng thành hai phần: Phần bên trong và phần bên ngoài. Trong khi ranh giới “vòng tròn” của hình, “vòng tròn” bao gồm cả ranh giới và bên trong.
Như vậy, Đường tròn là khoảng trống chứa tất cả các điểm trên một mặt phẳng, cách đều một điểm cho trước một khoảng cho trước. Điểm gọi trước là tâm của đường tròn, khoảng cách đã cho là bán kính của đường tròn. Nửa hình tròn còn được gọi là hình bán nguyệt
Tính chất của hình tròn là gì?
Đường tròn là hình có diện tích lớn nhất với chu vi cho trước.
Đường tròn có tính đối xứng cao: mỗi đường đi qua tâm tạo thành một phần đối của gương và nó có phần quay. Nhóm đối xứng của đường tròn là nhóm trực tâm O(2,R). Nhóm xoay là nhóm hình tròn T (“nhóm hình tròn”).
Tất cả các hình tròn đều giống nhau.
Chu vi của hình tròn tỉ lệ với bán kính bằng hằng số 2π.
Diện tích của hình tròn tỉ lệ với bình phương bán kính theo hằng số π.
Đường tròn có tâm trùng gốc và bán kính bằng 1 gọi là đường tròn đơn vị.
Đường tròn lớn của cấu hình đơn vị là đường tròn Riemann.
Qua ba điểm không thẳng hàng tồn tại đúng một đường tròn đi qua cả ba điểm đó.
Trong hệ tọa độ Descarter, ta có thể xác định được phương trình tâm và bán kính của đường tròn khi biết tọa độ của 3 điểm. Xem các đường ngoại vi.
3. Đường kính là gì?
Đường kính hình tròn: chính là đoạn thẳng đi qua tâm đường tròn và cắt đường tròn tại hai điểm. Đường kính hình trơn được kí hiệu là: d
Tinh chất của đường kinh là gì?
Đường kính là trường hợp đặc biệt của dây cung đi qua tâm đường tròn. Độ dài đường kính hình tròn gấp 2 lần bán kính hình tròn.
Đường kính là trường hợp đặc biệt của dây cung đi qua tâm đường tròn.
Đường kính là đoạn thẳng dài nhất đi qua hình tròn và chia hình tròn thành hai nửa bằng nhau.
Độ dài đường kính của hình tròn bán kính gấp 2 lần bán kính hình tròn đó.
Vậy làm thế nào để tinh được đường kính hình tròn?
Nếu bạn biết số đo bán kính của hình tròn, hãy nhân đôi nó để có đường kính Nếu bạn biết chu vi của hình tròn, hãy chia nó cho π để có đường kính Nếu bạn biết diện tích của hình tròn, hãy chia giá trị này cho π rồi lấy căn chia cho hai kết quả để tính bán kính của hình tròn, sau đó nhân bán kính với 2 để tìm đường kính.
4. Tìm hiểu về bán kính hình tròn:
Bán kính của hình tròn là khoảng cách từ tâm của hình tròn đến hình tròn.
Kí hiệu bán kính: r hoặc R
Cách tính bán kính hình tròn: Nếu biết chiều dài của đường kính, hãy chia chiều dài của đường kính cho 2 để có được chiều dài của bán kính. Nếu biết chu vi hình tròn, hãy chia chu vi cho 2π để được độ dài bán kính. Nếu bạn biết cách chia một hình tròn, hãy lấy phép chia này cho π sau đó lấy căn bậc hai để tăng độ dài bán kính.
5. Tâm đường tròn là gì?
Tâm của đường tròn là điểm chính giữa của đường tròn. Tâm của đường tròn cách tất cả các điểm trên đường tròn một khoảng bằng nhau. Từ điểm này đến các điểm trên đường tròn đều có các đoạn thẳng bằng nhau; Chúng ta gọi nó là bán kính. Nếu một đường thẳng đi qua tâm của đường tròn và cắt đường tròn tại hai điểm thì đoạn thẳng tạo thành từ hai điểm đó là đường kính của đường tròn
Tìm tâm đường tròn bằng cách vẽ hình Nếu chỉ là bài toán đơn giản về tìm tâm đường tròn, học sinh có thể sử dụng các cách sau để xác định tâm đường tròn: 1. Dùng compa để vẽ đường tròn: tâm của đường thẳng: Đường tròn của đường tròn là điểm đặt trụ la bàn. 2. Sử dụng dây cung của đường tròn: Vẽ hai dây cung song song và có độ dài bằng nhau gọi là AB và CD (Dây cung là đoạn thẳng nối hai điểm trên đường tròn). Nối A với D và B với C sao cho hai đoạn thẳng AD cắt BC tại điểm O. O là tâm của đường tròn 3. Vẽ hai đường tròn cắt nhau: Trình tự các bước vẽ hai đường tròn cắt nhau chính xác là định tâm của hình bao gồm: Vẽ dây nối 2 điểm trên đường tròn. Sử dụng thước kẻ để vẽ một đường bên trong vòng tròn, từ bên này sang bên kia. Vị trí của các điểm được chọn là không quan trọng. Gọi hai điểm này là A và B .
Dùng compa vẽ hai đường tròn cắt nhau. Hai vòng tròn này phải có cùng kích thước, lấy điểm A là tâm của một vòng tròn và điểm B là tâm của vòng tròn kia. Vẽ sao cho hai đường tròn này cắt nhau.
Vẽ một đường thẳng đứng qua hai giai đoạn của các vòng tròn. Sẽ có một điểm ở trên và dưới của các đường tròn giao nhau. Dùng thước kẻ để đảm bảo đường thẳng đi chính xác qua các điểm này. Gọi C và D là hai giao điểm của đường thẳng vừa vẽ và đường tròn thứ nhất. Vẽ hai đường viền mới. sử dụng la bàn vẽ hai đường kính có bán kính bằng nhau: một đường tròn có tâm là điểm C và đường tròn kia có tâm là điểm D. Như trên, hai đường tròn này phải giao nhau. C và D là giao điểm của đường thẳng đứng và đường tròn tâm.
Vẽ một đường đi qua hai giao điểm của các đường mới. Đường ngang này sẽ cắt qua các phần chồng chéo của hai đường mới. Đường ngang này sẽ cắt qua các phần chồng chéo của hai vòng tròn mới.
Giao điểm của hai đường kính chính là tâm của đường tròn ban đầu.
6. Bài tập về Hình tròn:
Câu 1. Tìm chu vi và diện tích hình tròn có:
a) r = 5cm ; r = 0,8cm ; r = 4/5 dm.
b) d = 5,2m ; d = 1,2m ; d = 3/5 dm.
Câu 2. Tính đường kính hình tròn có chu vi: C = 12,56cm; C = 18,84dm; C = 2,826m.
Câu 3. Tính diện tích hình tròn có chu vi: C = 6,908 m; C = 25,12dm; C = 16,956cm.
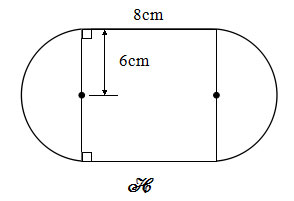
Câu 4. Diện tích hình H đã cho là tổng diện tích hình chữ nhật và hai nửa hình tròn. Tìm diện tích hình H
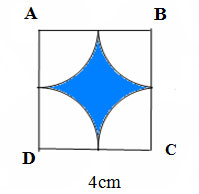
Câu 5. Cho hình vuông ABCD có cạnh 4cm. Tính diện tích phần tô đậm của hình vuông ABCD (xem hình vẽ)