Dưới đây là bài viết về: Đề thi giữa học kì 2 Toán 7 năm 2023 - 2024 có đáp án cùng với đó là đề cương ôn tập giúp các em chuẩn bị sẵn sàng khi làm bài thi trực tiếp, mời bạn theo dõi.
Mục lục bài viết
1. Đề cương ôn thi giữa học kì 2 Toán 7 năm 2023 – 2024:
I. Đại số:
– Tỉ lệ thức và dãy tỉ số bằng nhau: Tỉ lệ thức là một quan hệ giữa các số, trong đó hai số được so sánh với nhau. Tỉ số là kết quả của phép chia giữa hai số. Nếu tỉ lệ thức giữa hai bộ số là bằng nhau, tức là hai tỉ số của chúng cũng bằng nhau, ta có quan hệ “tỉ lệ thức và dãy tỉ số bằng nhau”.
– Giải toán về đại lượng tỉ lệ: Đây là loại toán liên quan đến việc giải quyết các vấn đề liên quan đến tỉ lệ giữa các đại lượng. Ví dụ, có thể yêu cầu tính tỉ lệ giữa các đại lượng khác nhau, tìm giá trị của một đại lượng dựa trên tỉ lệ của các đại lượng khác, hay giải quyết các bài toán về tỉ lệ phần trăm, tỉ lệ hỗn hợp, tỉ lệ tăng/giảm, và nhiều loại bài toán khác.
II. Hình học:
– Quan hệ giữa đường vuông góc và đường xiên: Đường vuông góc là một đường có góc giữa nó và một đường khác là 90 độ. Đường xiên là đường nối hai điểm không nằm trên cùng một đường thẳng trong một hình học nào đó. Quan hệ giữa đường vuông góc và đường xiên là khi một đường xiên cắt qua một đường vuông góc, nó sẽ tạo thành hai góc vuông bằng nhau.
– Các đường đồng quy của tam giác: Đường đồng quy của tam giác là những đường đi qua các đỉnh của tam giác mà khi nối các đỉnh của tam giác với các điểm cắt này thì các đoạn thẳng này đồng quy, tức là cắt nhau tại một điểm duy nhất hoặc chạm vào một điểm duy nhất trên cung của đường đồng quy. Các đường đồng quy của tam giác bao gồm đường cao, đường trung trực, đường phân giác, đường trung bình, và đường đồng quy của trực tâm.
– Giải bài toán có nội dung hình học và vận dụng giải quyết vấn đề thực tiễn liên quan đến hình học:
+ Ví dụ về bài toán hình học có vận dụng thực tiễn là bài toán về tính diện tích của một khu đất hoặc một diện tích bất kỳ, dựa trên các thông tin hình học như độ dài, độ rộng của khu đất, hoặc các kích thước của các đối tượng trong không gian thực tế.
+ Ví dụ, giả sử bạn cần tính diện tích của một khu đất hình chữ nhật để biết được số lượng vật liệu cần thiết để xây dựng trên đó. Bạn có thể sử dụng kiến thức về hình học để tính toán diện tích của khu đất đó, trong đó chiều dài và chiều rộng của khu đất sẽ là đại lượng được sử dụng trong bài toán. Bạn có thể áp dụng công thức tính diện tích của hình chữ nhật là Diện tích = Chiều dài x Chiều rộng để giải quyết bài toán này.
+ Ví dụ cụ thể về việc vận dụng giải quyết vấn đề thực tiễn liên quan đến hình học có thể là trong lĩnh vực kiến trúc. Giả sử bạn đang thiết kế một công trình xây dựng và cần tính toán lượng vật liệu cần thiết để xây dựng một mô hình của công trình đó. Bạn có thể sử dụng kiến thức về hình học để tính toán các thông số như diện tích sàn, diện tích tường, chiều cao của công trình, v.v.
Ngoài ra, còn nhiều bài toán hình học khác có thể được áp dụng vào các vấn đề thực tiễn như tính diện tích của một vườn trồng cây, tính thể tích của một hộp, tính độ dài của đường ống nước, tính tỷ lệ các thành phần trong một hỗn hợp, v.v. Việc vận dụng giải quyết các vấn đề thực tiễn liên quan đến hình học có thể giúp giải quyết các vấn đề thực tế trong nhiều lĩnh vực như kiến trúc, xây dựng, địa lý, công nghệ, khoa học môi trường, v.v.
2. Đề thi giữa học kì 2 Toán 7 năm 2023 – 2024 có đáp án:
2.1 Đề thi:
PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên ta được
A. 12,5 : 34,5;
B. 29 : 65;
C. 25 : 69;
D. 1 : 3.
Câu 2. Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
A. –6;
B. 0;
C. –9;
D. –1.
Câu 3. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
A. –32;
B. 32;
C. –2;
D. 2.
Câu 4. Cho hình vẽ sau:
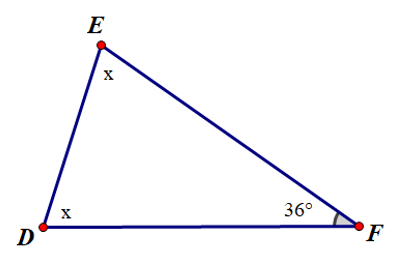
Số đo x là
A. 18°;
B. 72°;
C. 36°;
D. Không xác định được.
Câu 5. Hai tam giác bằng nhau là
A. Hai tam giác có ba cặp cạnh tương ứng bằng nhau;
B. Hai tam giác có ba cặp góc tương ứng bằng nhau;
C. Hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau;
D. Hai tam giác có hai cạnh bằng nhau.
Câu 6. Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là
A. 50°;
B. 40°;
C. 140°;
D. 100°.
Câu 7. Cho tam giác MNP có: MN < MP, MD ⊥ NP. Khẳng định nào sau đây là đúng?
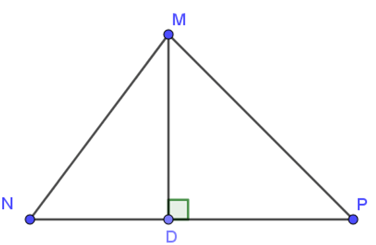
A. DN = DP;
B. MN = MP;
C. MD > MN;
D. MD < MP.
Câu 8. Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
A. Trung trực;
B. Giao điểm;
C. Trọng tâm;
D. Trung điểm.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Tìm số hữu tỉ x trong các tỉ lệ thức sau:
c)
Bài 2. (2,0 điểm)
a. Tìm hai số a, b biết rằng 2a = 5b và 3a + 4b = 46
b. Tìm ba số a, b, c biết rằng a : b : c = 2 : 4 : 5 và a + b – c = 3
Bài 3. (1,5 điểm) Trong đợt quyên góp sách ủng hộ các bạn vùng cao, số sách mà ba lớp 7A, 7B, 7C quyên góp được tỉ lệ với ba số 5; 6; 8. Tính số sách cả ba lớp đã quyên góp, biết số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là 24 quyển.
Bài 4. (3,0 điểm)
Cho tam giác ABC (AB < AC) M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho AM = EM.
a. Chứng minh: ΔAMB = ΔMCE
b. Từ A kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Chứng minh: CE = BD
c. Tam giác AMD là tam giác gì? Vì sao?
2.2. Đáp án:
I. Trắc nghiệm
1. C | 2. A | 3. A | 4.B | 5. C | 6. D | 7. D | 8. D |
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
Vậy
Vậy
c.
3(x + 11) = 2(14 – x)
3x + 33 = 28 – 2x
3x + 2x = 28 – 33
5x = –5
x = –1
Vậy x = –1.
Bài 2. (1,5 điểm)
a) Ta có: 2a = 5b
Lại có:
=> 3a = 2. 15 = 30 => a = 10
4b = 2. 8 = 16 => b = 4.
b) a : b : c = 2 : 4 : 5
=> a = 2. 3 = 6
b = 4. 3 = 12
c = 5. 3 = 15
Bài 3. (1,5 điểm)
Gọi số sách 3 lớp 7A, 7B, 7C quyên góp được là x, y, z (quyển) ()
Vì số sách mà ba lớp 7A,7B,7C quyên góp được tỉ lệ với ba số 5;6;8 nên
Mà số sách lớp 7C quyên góp nhiều hơn số sách của lớp 7A quyên góp là 24 quyển nên z – x = 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Vậy số sách 3 lớp 7A,7B,7C quyên góp được lần lượt là 40 quyển; 48 quyển và 64 quyển.
Bài 4. (3,0 điểm)
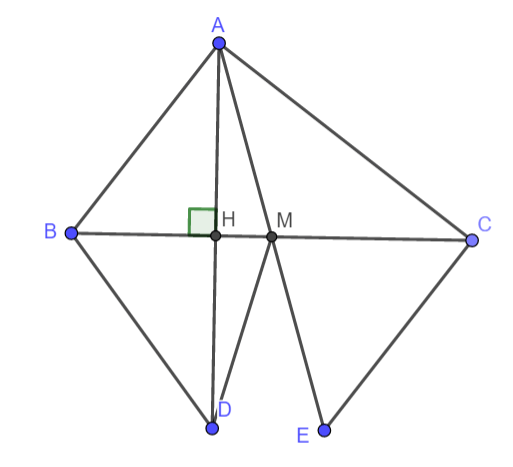
a. Xét tam giác ABM và tam giác MEC có:
BM = MC (M là trung điểm BC)
(đối đỉnh)
AM = ME (gt)
=> ΔAMB = ΔMCE (c – g – c)
b. Xét tam giác ABH vuông tại H và tam giác BHD vuông tại H có:
BH là cạnh chung
AH = DH (gt)
=> ΔABH = ΔBDH
=> AB = BD (1)
Ta lại có: ΔAMB = ΔMCE (cmt) => AB = CE (2)
Từ (1) và (2) suy ra CE = BD
c. Từ câu b ta dễ dàng suy ra MA = MD
Vậy tam giác AMD là tam giác cân tại M.
3. Ma trận đề thi giữa học kì 2 Toán 7 năm 2023 – 2024 có đáp án:
Ma trận đề thi giữa kì 2 Toán 7
TT | Chủ đề | Nội dung/Đơn vị kiến thức | Mức độ đánh giá | Tổng % điểm | |||||||
Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | ||||||||
TNKQ | TL | TNKQ | TL | TNKQ | TL | TNKQ | TL | ||||
1 | Tỉ lệ thức và đại lượng tỉ lệ (12 tiết) | 1. Tỉ lệ thức và dãy tỉ số bằng nhau | 6 (1,5đ) |
|
|
|
|
|
| 1 (1đ) | 25 |
2. Giải toán về đại lượng tỉ lệ |
|
|
| 2 (2đ) |
|
|
|
| 20 | ||
2
| Quan hệ giữa các yếu tố trong một tam giác (13 tiết) | 1. Quan hệ giữa đường vuông góc và đường xiên. Các đường đồng quy của tam giác. | 6 (1,5đ) |
|
| 1 (2đ) |
|
|
|
|
35 |
2. Giải bài toán có nội dung hình học và vận dụng giải quyết vấn đề thực tiễn liên quan đến hình học. |
|
|
|
|
| 1 (2đ) |
|
|
20 | ||
Tổng | 12 (3đ) |
|
| 3 (4đ) |
| 1 (2đ) |
| 1 (1đ) |
| ||
Tỉ lệ % | 30% | 40% | 20% | 10% | 100 | ||||||
Tỉ lệ chung | 70% | 30% | 100 | ||||||||




