Chuyển phương trình tham số sang phương trình tổng quát

1. Chuyển phương trình tham số sang phương trình tổng quát:

Để chuyển từ phương trình tham số sang phương trình tổng quát của một đường thẳng, ta thực hiện các bước sau một cách cẩn thận và chi tiết:

Bước 1: Xác định hai điểm thuộc đường thẳng. Chọn hai điểm trên đường thẳng và gán chúng là A có tọa độ (x1, y1) và B có tọa độ (x2, y2).

Bước 2: Tính toán độ dài và hướng của đoạn thẳng AB. Để tính độ dài của đoạn thẳng AB, ta sử dụng công thức khoảng cách giữa hai điểm trong không gian hai chiều:

AB = √((x2 – x1)^2 + (y2 – y1)^2)

Sau đó, để xác định hướng của đoạn thẳng AB, ta sử dụng các hệ số cosin và sin của góc giữa đoạn thẳng và trục Ox:

cosθ = (x2 – x1)/AB

sinθ = (y2 – y1)/AB

Bước 3: Viết phương trình tham số của đường thẳng. Sử dụng hướng và độ dài đã tính ở bước trước, chúng ta có thể viết phương trình tham số của đường thẳng dưới dạng:

x = x1 + t(x2 – x1)

y = y1 + t(y2 – y1)

Ở đây, t là tham số của phương trình, cho phép chúng ta di chuyển dọc theo đường thẳng.

Bước 4: Chuyển đổi phương trình tham số thành phương trình tổng quát. Để làm điều này, ta cần loại bỏ tham số t bằng cách giải hệ phương trình đồng thời của hai phương trình x = x1 + t(x2 – x1) và y = y1 + t(y2 – y1) để tìm ra giá trị của x và y. Sau đó, chúng ta sẽ thu được phương trình tổng quát của đường thẳng dưới dạng: ax+by+c=0

Trong đó:

a = y2 – y1

b = -(x2 – x1)

c = x2y1 – x1y2

Ví dụ, để minh họa quá trình này, giả sử chúng ta có đường thẳng AB với điểm A có tọa độ (-1, 3) và điểm B có tọa độ (4, 7). Sau khi tính toán, ta có:

AB = √((4 – (-1))^2 + (7 – 3)^2) = √(25 + 16) = √41

cosθ = (4 – (-1))/√41 = 5/√41

sinθ = (7 – 3)/√41 = 4/√41

Sau đó, ta viết phương trình tham số của đường thẳng AB:

x = -1 + 5/√41 t

y = 3 + 4/√41 t

Cuối cùng, chúng ta chuyển đổi phương trình tham số thành phương trình tổng quát của đường thẳng AB:

a = y2 – y1 = 7 – 3 = 4

b = -(x2 – x1) = -((4) – (-1)) = -5

c = x2y1 – x1y2 = (4)(3) – (-1)(7) = -4

Vậy phương trình tổng quát của đường thẳng AB là: 4x – 5y – 4 = 0.

 2. Ví dụ minh họa về Chuyển phương trình tham số sang phương trình tổng quát:

Ví dụ 1: Cho đường thẳng d: 2x – 3y + 6 = 0. Viết phương trình đường thẳng d dưới dạng tham số?

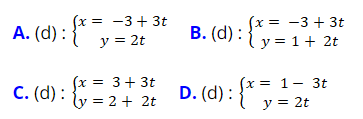
Lời giải

+ Đường thẳng d: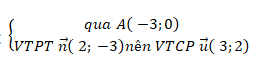 

⇒ Phương trình tham số của đường thẳng d:

Chọn A.

Ví dụ 2: Cho đường thẳng d: . Viết phương trình tổng quát của đường thẳng d.

A. x + 2y – 1 = 0   B. x – 2y + 3 = 0

C. 2x + y – 7 = 0   D. 2x – y + 7 = 0

Lời giải

+ Đường thẳng d:

⇒ Phương trình tham số của đường thẳng d:

2(x -3) + 1(y-1) = 0 hay 2x + y -7 = 0.

Chọn A.

Ví dụ 3: Cho đường thẳng ( d) : 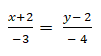. Viết phương trình đường thẳng d dạng tổng quát?

A. 4x – 3y + 2 = 0    B. 4x – 3y + 14 = 0    C. 3x + 4y – 2 = 0    D. Đáp án khác

Lời giải

Đường thẳng d:

⇒ Phương trình tổng quát của đường thẳng d:

4( x + 2) – 3( y – 2) = 0 hay 4x – 3y + 14 = 0

Chọn B.

Ví dụ 4: Cho đường thẳng d: 3x – y + 6 = 0 .Viết phương trình đường thẳng d dưới dạng chính tắc?

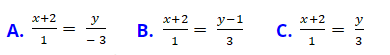D. Không có phương trình chính tắc

Lời giải

Đường thẳng d: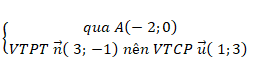

⇒ Phương trình chính tắc của đường thẳng d:

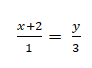
Chọn C.

Ví dụ 5: Cho đường thẳng d: 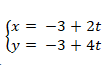Viết phương trình đường thẳng d dưới dạng chính tắc?

Lời giải

Đường thẳng d:

⇒ Phương trình chính tắc của đường thẳng d:

Chọn A.

Ví dụ 6: Cho đường thẳng ( d): 2x – y + 6 = 0. Viết phương trình đường thẳng d dạng chính tắc?

Lời giaỉ

Đường thẳng d:

⇒ Phương trình chính tắc của đường thẳng d: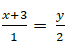

Chọn B

Ví dụ 7: Cho đường thẳng d: C.Viết phương trình đường thẳng d dưới dạng tham số?

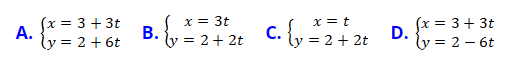
Lời giải

Đường thẳng d:

⇒ Phương trình tham số của đường thẳng d: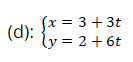

(d): Cách chuyển dạng phương trình đường thẳng: tổng quát sang tham số, chính tắc

Chọn A.

Ví dụ 8: Cho tam giác ABC có M , N và P lần lượt là trung điểm của AB; BC và AC. Viết phương trình chính tắc và tổng quát của đường thẳng AB biết M(0; -2); N( -2; 3) và P( 2; 1)?

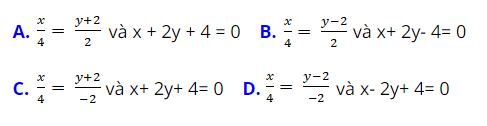
Lời giải

+ Do N và P lần lượt là trung điểm của BC và AC

⇒ NP là đường trung bình của tam giác BAC.

⇒ NP// AB.

+ Đường thẳng AB :

⇒ Phương trình chính tắc của AB:  x/4 = (y+2)/ (-2)

Phương trình tổng quát của AB: 1( x – 0) + 2(y + 2) = 0 hay x + 2y + 4 = 0.

Chọn C.

3. Bài tập vận dụng liên quan có đáp án:

Bài 1: Cho đường thẳng d: 3x – 2y + 1 = 0. Viết phương trình tham số của đường thẳng d.

Lời giải:

Biết đường thẳng d: 3x – 2y + 1 = 0

Ta có:

Điểm A(1; 2) thuộc đường thẳng d do 3.1 – 2.2 + 1 = 0

Vectơ pháp tuyến của d là  →n=( 3 ; − 2)⇒ Vectơ chỉ phương của d là: →u=(2;3)

Phương trình tham số của đường thẳng d là: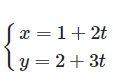

Bài 2: Cho đường thẳng d: 4x + 4 = 0. Viết phương trình tham số của đường thẳng d.

Lời giải:

Biết đường thẳng d: 4x + 4 = 0

Ta có:

Điểm B(-1; 3) thuộc đường thẳng d do 4.(-1) + 4 = 0

(có thể lấy tung độ bất kì vì phương trình đường thẳng d không phụ thuộc tung độ y)

Vectơ pháp tuyến của d là  →n=(4;0)⇒ Vectơ chỉ phương của d là: →u=(0;−4)

Phương trình tham số của đường thẳng d là: 

Bài 3: Cho đường thẳng d: . Viết phương trình tổng quát của đường thẳng d.

Lời giải:

Biết đường thẳng d: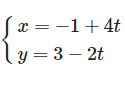 

Ta có:

Điểm C(-1; 3) thuộc vào đường thẳng d dựa vào phương trình tham số. (cho t = 0 thay vào phương trình tham số của d, ta tìm được tọa độ C)

Vectơ chỉ phương của d là  →u = (4 ; −2)⇒Vectơ pháp tuyến của d là → n = (2 ; 4)

Phương trình tổng quát của d là:

2 (x + 1) + 4 (y – 3)  = 0

⇔⇔ 2x + 4y – 10 = 0

⇔⇔x + 2y – 5 = 0

Bài 4: Cho đường thẳng d: – 2x – 3y + 6 = 0 .Viết phương trình đường thẳng d dưới dạng chính tắc?

A.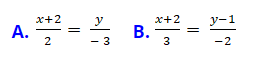    

C. 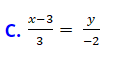    D. Không có phương trình chính tắc

Lời giải:

Đáp án: C

Đường thẳng d: 

⇒ Phương trình chính tắc của đường thẳng d:

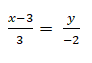
Bài 5: Cho đường thẳng d: 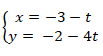 . Viết phương trình đường thẳng d dưới dạng chính tắc?

Lời giải:

Đáp án: A

Đường thẳng d: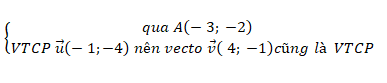 

⇒ Phương trình chính tắc của đường thẳng d:

(x+3)/4 = (y+2)/1

Câu 6: Cho đường thẳng ( d): -2x + 3y + 6 = 0. Viết phương trình đường thẳng d dạng chính tắc?

Lời giải:D

Đáp án: B

Đường thẳng d: 

⇒ Phương trình chính tắc của đường thẳng d:

(x-3)/3 = y/2

Câu 7: Cho đường thẳng d: (x-10)/10 = (y=10)/10 .Viết phương trình đường thẳng d dưới dạng tham số?

Lời giải:

Đáp án: A

Đường thẳng d: 

⇒ Phương trình tham số của đường thẳng (d):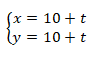 

Câu 8: Cho đường thẳng d: x / 2 + y / (-3) = 1. Viết phương trình đường thẳng d dạng chính tắc?

A. (x + 1) / 2 = (y + 1) / (-3)   B. (x + 1) / 2 = (y + 1) / 2    C. ( x – 2) / 2 = y / (-3)    D. (x – 2) / 2 = y / 3

Lời giải:

Đáp án: D

+ Ta đưa đường thẳng d về dạng tổng quát :

x / 2 + y / (-3) = 1 ⇔ – 3x + 2y + 6 = 0

+ Đường thẳng d đi qua M( 2;0) và VTPT n→( -3;2) nên một VTCP u→( 2; 3) .

⇒ Phương trình đường thẳng d dạng chính tắc : (x – 2) / 2 = y / 3

THAM KHẢO THÊM:

• Xác định tham số, cách tìm m để hàm số liên tục cực hay
• Viết phương trình tổng quát của đường thẳng Ox và Oy