Cho tam giác ABC – Các bài toán hình lớp 7 về tam giác

1. Lý thuyết về hình tam giác toán lớp 7:

a, Hình tam giác ABC có:

– Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.

– Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C.

– Ba góc là:

Góc đỉnh A, cạnh AB và AC (gọi tắt là góc A);

Góc đỉnh B, cạnh BA và BC (gọi tắt là góc B);

Góc đỉnh C, cạnh AC và CB (gọi tắt là góc C).

b) Đáy và đường cao

c, Chu vi hình tam giác

Công thức tính chu vi hình tam giác thường: P = a + b + c

Trong đó:

P là chu vi tam giác.

a, b, c là 3 cạnh của hình tam giác đó.

d, Diện tích hình tam giác

Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2

(S là diện tích, a là độ dài đáy, h là chiều cao)

Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho 2.

Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là 13cm và chiều cao là 8cm.

Phương pháp giải: Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2.

Cách giải:

Diện tích hình tam giác đó là:

13 x 8 : 2 = 52 (cm2)

Đáp số: 52cm2

d, Dấu hiệu phân biệt hình tam giác:

Tam giác vuông sẽ có một góc vuông.

Tam giác có hai góc nhọn bù nhau là tam giác vuông.

Tam giác có đường trung tuyến bằng một nửa cạnh đó là tam giác vuông.

Tam giác có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh còn lại là tam giác vuông.

Nếu một tam giác nội tiếp trong một đường tròn có một cạnh là đường kính thì tam giác đó vuông.

2. Cho tam giác ABC – Các bài toán hình lớp 7 về tam giác:

Câu 1. Cho tam giác ABC vuông ở A(AB < AC), đường cao AH, biết AB = 6cm. Đường trung trực của BC cắt các đường thẳng AB, AC, BC theo thứ tự ở D, E và F biết DE = 5cm, EF = 4cm. Chứng minh:

a) Tam giác FEC đồng dạng với tam giác FBD

b) Tam giác AED đồng dạng với tam giác HAC

c) Tính BC, AH, AC

Hướng dẫn giải

a. Ta có:

Mà

Xét tam giác ABC vuông tại A ta có:

(Pitago)

Xét tam giác CAH vuông tại H và tam giác CBA vuông tại A có:

 Góc ECF chung

Bài 2:

Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC.

a) Chứng minh tam giác BEM bằng tam giác CFM

b) Chứng minh AM vuông góc với EF

c) Từ B kẻ đường thẳng vuông góc với AB tại B từ C kẻ đường vuông góc với AC tại C, 2 đường thẳng này cắt nhau tại D. Chứng minh rằng 3 điểm A, M, D thẳng hàng.

Hướng dẫn giải

a. Xét tam giác BEM và CFM ta có:

BM = CM (vì AM là trung tuyến ứng với BC)

(vì tam giác ABC cân ở A)

(cạnh huyền – góc nhọn)

b. Từ câu a ta có

Ta có: AE = AB – BE

Lại có: AF = AC – CF

Mà AB = AC, BE = CF

Vậy AE = AF

Trong một tam giác cân đường trung tuyến đồng thời là đường phân giác, đường trung trực, …. Nên AM là phân giác góc A

Xét tam giác AEI và tam giác AFI ta có:

AI là cạnh chung

AE = AF

Vậy AM vuông góc với FE

c. Theo câu a ta có

Vậy M thuộc phân giác góc A (1)

Xét tam giác vuông ABD và ACD có

AD là cạnh chung

(Cạnh huyền – góc nhọn)

Suy ra DB = DC nên D thuộc tia phân giác góc A (2)

Từ (1) và (2) ta có A, D, M thẳng hàng

Bài 3:

Cho ΔABC. Gọi I là 1 điểm trên cạnh BC. Qua I kẻ đường thẳng song song với cạnh AC cắt AB tại M. Qua I kẻ đường thẳng song song với cạnh AB cắt AC tại N.

a, Gọi O là trung điểm của cạnh AI. Chứng minh rằng ba điểm M, N, O thẳng hàng

b, Kẻ MH, NK, AD vuông góc với BC lần lượt tại H, K, D. Chứng minh rằng MH + NK = AD

c, Tìm vị trí của I để MN // BC

Bài 4. Cho tam giác ABC cân tại A có hai đường cao AH và BI cắt nhau tạo O và AB = 5cm, BC = 6cm. Tia BI cắt đường phân giác ngoài của góc A tại M

a) Tính AH?

b) Chứng tỏ: AM^2 = OM.MI

c) Tam giác MAB ~ tam giác AOB

d) IA.MB = 5.IM

Hướng dẫn giải

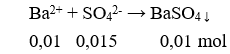
a. Xét tam giác AHC vuông, áp dụng định lí Pitago ta dễ dàng tính được AH = 4

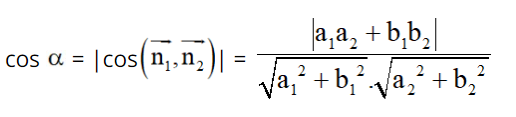
Xét tam giác BOA và tam giác BAM có:

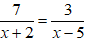
Bài 5. Cho tam giác DEF vuông tại D, đường cao DH và DE = 6cm, EF = 9cm.

a. Chứng minh: Tâm giác DEF đồng dạng tam giác HED.

b. Chứng minh: DF^2 = FH.EF.

c. Qua D kẻ đường thẳng a, từ E dựng EP và từ F dựng FQ vuông góc với a (P, Q thuộc a). Chứng minh:

Hướng dẫn giải

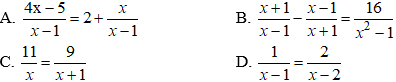
Bài 6.

Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm và AH là đường cao

a. Chứng minh tam giác HBA đồng dạng với tam giác ABC.

b. Chứng minh: AB² = HB . BC

c. Kẻ tia phân giác góc A cắt BC tại I. Tính độ dài cạnh BI.

Hướng dẫn giải:

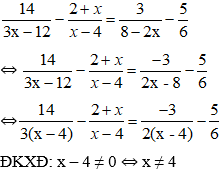
a, Xét tam giác HBA và tam giác ABC: góc B chung H = A = 90 => tg HBA đồng dạng ABC.

b, Vì tam giác BHA đồng dạng tg ABC: => AB/HB = BC/AB => đpcm.

c, Áp dụng tính chất tia phân giác:

=>AB/AC = BI/IC => BI/AB = IC/AC

Áp dụng tính chất dãy tỉ số bằng nhau:

BI/AB = IC/AC = BI + IC/AB + AC = BC/AB + AC = 10/6 + 8 = 5/7

Suy ra:

BI = 5/7.6 = 4,3

IC = 5/7.8 = 5,7

Bài 7

Cho tam giác ABC vuông tại góc A, đường cao AH (H thuộc BC) và phân giác BE của ABC (E thuộc AC) cắt nhau tại I. Chứng minh:

a. IH.AB = IA.BH

b. Tam giác BHA bằng tam giác BAC,

c. IH/IA = AE/EC

d. Tam giác AIE cân

Hướng dẫn giải

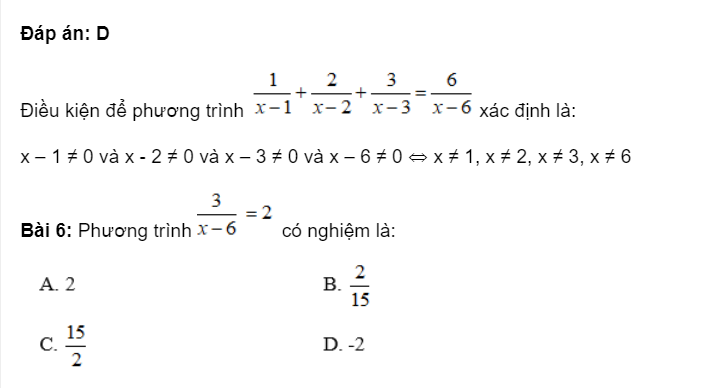
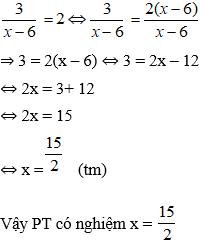
c. Ta có:

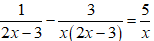
d. Ta có:

3. Bài tập tự luyện:

Bài 1: Cho tam giác ABC cân tại A (góc A <90 độ). Kẻ BD vuông góc với AC, CE vuông góc với AB (E thuộc cạnh AB, D thuộc cạnh AC)

a) Chứng minh ∆ABD = ∆ACE

b) Gọi I là giao điểm của BD và CE. Chứng minh AI là tia phân giác của góc CAB

c) Chứng minh 2IB > BC

Bài 2: Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm.

a. Chứng minh rằng tam giác ABC là tam giác vuông tại A.

b. Vẽ phân giác BE của góc B (E thuộc AC), từ E kẻ EP vuông góc với BC (P thuộc BC). Chứng minh EA = EP.

Bài 3: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính khoảng cách từ trọng tâm G của tam giác ABC đến các đỉnh của tam giác.

Bài 4: Cho tam giác ABC vuông tại A. Biết AB = 6cm, AC = 8cm. Đường thẳng đi qua trung điểm M của BC và vuông góc với BC cắt AC tại N.

a. Tính độ dài cạnh BC.

b. Chứng minh góc CBN bằng góc NCB.

c. Trên tia đối của tia NB lấy điểm F sao cho NF = NC. Chứng minh rằng tam giác BEC vuông.

Bài 5: Cho tam giác ABC vuông tại A, biết AB = 5cm, BC = 13cm.

a. Tính AC.

b. Kẻ AH vuông góc với BC. Tính AH, BH, CH.

c. Gọi M là trung điểm BC. Tính AM.

d. Trên tia đối tia MA lấy E sao cho ME = MA. Chứng minh BE = AC và BE // AC.