Xác định vị trí tương đối của hai đường thẳng là một trong những khái niệm quan trọng trong toán học. Để hiểu rõ hơn về khái niệm này, trong bài viết dưới đây hãy cùng chúng tôi tìm hiểu cách xác định vị trí tương đối của hai đường thẳng chuẩn nhất.
Mục lục bài viết
1. Xác định vị trí tương đối của hai đường thẳng trong trường hợp a1.b1.c1 ≠ 0:
Cho hai đường thẳng d1: a1x + b1y + c1 = 0 và d2: a2x + b2y + c2 = 0. Xét vị trí tương đối của hai đường thẳng d1 và d2: Áp dụng trong trường hợp a1.b1.c1 ≠ 0: Nếu 
thì d1 ≡ d2. Nếu 
thì d1 // d2. Nếu 
thì d1 cắt d2.
2. Xác định vị trí tương đối của hai đường thẳng dựa vào số điểm chung của hai đường thẳng:
Cho hai đường thẳng d1: a1x + b1y + c1 = 0 và d2: a2x + b2y + c2 = 0. Xét vị trí tương đối của hai đường thẳng d1 và d2: Dựa vào số điểm chung của hai đường thẳng trên ta suy ra vị trí tương đối của hai đường thẳng: Giao điểm của hai đường thẳng d1 và d2( nếu có) là nghiệm hệ phương trình: 
Khi xét vị trí tương đối của hai đường thẳng d1 và d2, chúng ta có một số trường hợp khác nhau:
– Nếu hai đường thẳng cắt nhau tại một điểm duy nhất, ta nói rằng chúng có giao điểm. Điều này xảy ra khi hệ phương trình tương ứng với hai đường thẳng có một nghiệm duy nhất. Trong trường hợp này, ta có thể tìm được giá trị của x và y khi giải hệ phương trình.
– Nếu hai đường thẳng trùng nhau, tức là các điểm trên hai đường thẳng hoàn toàn trùng nhau và không có điểm nào riêng biệt. Khi giải hệ phương trình tương ứng, ta thu được vô số nghiệm. Điều này có nghĩa là mọi giá trị của x và y đều là nghiệm của hệ phương trình.
– Nếu hai đường thẳng song song, tức là chúng không cắt nhau và không có điểm chung nào. Trong trường hợp này, hệ phương trình tương ứng không có nghiệm.
Vì vậy, bằng cách xem xét số điểm chung và giải hệ phương trình tương ứng, chúng ta có thể xác định vị trí tương đối của hai đường thẳng d1 và d2.
3. Bài tập vận dụng liên quan:
Câu 1. Xét vị trí tương đối của hai đường thẳng d1: 3x – 2y – 6 = 0 và d2: 6x – 2y – 8 = 0. A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau. Đáp án: D.
Câu 2. Xét vị trí tương đối của hai đường thẳng d1: 
= 1 và d2: 3x + 4y – 10 = 0. A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau. Đáp án: C.
Câu 3. Đường thẳng nào sau đây song song với đường thẳng 2x + 3y – 1 = 0? A. 4x + 6y + 10 = 0 . B. 3x – 2y + 1 = 0 C. 2x – 3y + 1 = 0. D. 4x + 6y – 2 = 0 Đáp án: A.
Câu 4. Với giá trị nào của m thì hai đường thẳng a: 3x + 4y + 10 = 0 và b: (2m – 1)x + m2y + 10 = 0 trùng nhau? A. m = ± 2 B. m = ± 1 C. m = 2 D. m = -2 Đáp án: C
Câu 5. Với giá trị nào của m thì hai đường thẳng (a) : 2x + y + 4 – m = 0 và ( b) : (m + 3)x + y + 2m – 1 = 0 song song? A. m = 1 B. m = -1 C. m = 2 D. m = 3 Đáp án: B.
Câu 6: Xét vị trí tương đối của hai đường thẳng (a): 2x – 3y + 2 = 0 và (b): y – 2 = 0. A. Cắt nhau nhưng không vuông góc B. Song song C. Trùng nhau D. Vuông góc Đáp án: A.
Câu 7. Với giá trị nào của m thì hai đường thẳng ( a) : ( m- 3)x + 2y + m2 – 1 = 0 và (b): – x + my + m2 – 2m + 1 = 0 cắt nhau? A. m ≠ 1. B. m ≠ 1 và m ≠ 2 C. m ≠ 2 D. m ≠ 1 hoặc m ≠ 2 Đáp án: B.
Câu 8. Tìm tọa độ giao điểm của đường thẳng (a): 2x + 4y – 10 = 0 và trục hoành. A.(0;2) B. (0; 5) C. (2;0) D. (5;0) Đáp án: D.
Câu 9. Nếu ba đường thẳng (a): 2x + y- 4 = 0; (b) : 5x – 2y + 3 = 0 và (c): mx + 3y – 2 = 0 đồng quy thì m nhận giá trị nào sau đây? A. 12/5 B. – 12/5 C. 12 D. – 12 Đáp án: D.
Câu 10. Với giá trị nào của m thì ba đường thẳng (a): 3x – 4y + 15 = 0; (b): 5x + 2y – 1 = 0 và (c):mx – 4y + 15 = 0 đồng quy? A. m = -5 B. m = 5 C. m = 3 D. m = -3 Đáp án: C.
Câu 11: Xác định vị trí tương đối của 2 đường thẳng sau đây: (a) : x – 2y + 1 = 0 và (b): – 3x + 6y – 1 = 0 A. Song song. B. Trùng nhau. C. Vuông góc nhau. D. Cắt nhau. Đáp án: A
Câu 12: Đường thẳng (a) :3x – 2y – 7 = 0 cắt đường thẳng nào sau đây? A. ( d1) : 3x + 2y = 0 B. (d2) : 3x – 2y = 0 C. (d3): -3x + 2y – 7 = 0 D. (d4): 6x – 4y – 14 = 0 Đáp án: A
Câu 13: Hai đường thẳng (a): 4x + 3y – 18 = 0 và (b) : 3x + 5y – 19 = 0 cắt nhau tại điểm có toạ độ: A. (3; 2) B. ( -3; 2) C. ( 3; -2) D. (-3; -2) Đáp án: A
Câu 14: Phương trình nào sau đây biểu diễn đường thẳng không song song với đường thẳng d: y = 2x – 1 A. 2x – y + 5 = 0 B. 2x – y – 5 = 0 C. – 2x + y = 0 D. 2x + y – 5 = 0 Đáp án: D
Câu 15: Hai đường thẳng (a) : mx + y = m + 1 và (b): x + my = 2 song song khi và chỉ khi: A. m = 2 B. m = ± 1 C. m = -1 D. m = 1 Đáp án: C
Câu 16: Tìm tất cả các giá trị của m để hai đường thẳng (a): 2x – 3my + 10 = 0 và ( b) : mx + 4y + 1 = 0 cắt nhau. A. 1 < m < 10 B. m = 1 C. Không có m. D. Với mọi m. Đáp án: D
Câu 17: Với giá trị nào của m thì hai đường thẳng (a): mx + y – 19 = 0 và (b): ( m – 1).x + (m + 1).y – 20 = 0 vuông góc? A. Với mọi m. B. m = 2 C. Không có m. D. m = 1 Đáp án: C
Câu 18: Với giá trị nào của m thì hai đường thẳng ( a): 3mx + 2y + 6 = 0 và (b) : (m2 + 2)x + 2my + 6 = 0 cắt nhau? A. m ≠ ±3 B. m ≠ ±2 C. mọi m D. m ≠ ±1. Đáp án: D
Câu 19: Tìm tọa độ giao điểm của hai đường thẳng (a) 7x – 3y – 1 = 0 và (b): x + 2 = 0. A. (-2; 5) B. (-2; -5) C. (-2; -4) D. (-4; 3) Đáp án: B
Câu 20: Trong mặt phẳng với hệ tọa độ Oxy, cho ba đường thẳng lần lượt có phương trình (a) : 3x – 4y + 15 = 0, ( b): 5x + 2y – 1 = 0 và (c) : mx – (2m – 1)y + 9m – 13 = 0. Tìm tất cả các giá trị của tham số m để ba đường thẳng đã cho cùng đi qua một điểm. A. m =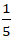 
B. m= -5 C. m= – 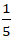D. m= 5 Đáp án: D
Câu 21: Cho 3 đường thẳng d1 : 2x + y – 1 = 0 ; d2 : x + 2y + 1 = 0 và d3 : mx – y – 7 = 0. Để ba đường thẳng này đồng qui thì giá trị thích hợp của m là: A. m= -6 B. m = 6 C. m = -5 D. m = 5 Đáp án: B
Câu 22. Xét vị trí tương đối của hai đường thẳng d1: x- 2y+ 1= 0 và d2: -3x + 6y- 10= 0 A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau. Đáp án: B.
Câu 25. Xác định vị trí tương đối của hai đường thẳng ∆1: 7x + 2y – 1 = 0 và ∆2: 
A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau. Đáp án: D.
Câu 26. Xét vị trí tương đối của hai đường thẳng d1: 
và d2: 3x + 2y – 14 = 0. A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau. Đáp án: A
Câu 27. Đường thẳng nào sau đây có đúng một điểm chung với đường thẳng d:
? A. 7x + 3y – 1 = 0 B. 7x + 3y + 1 = 0 C. 3x – 7y + 2018 = 0 D. 7x + 3y + 10 = 0 Đáp án: C.
Câu 28: Xét vị trí tương đối của hai đường thẳng d1: 
và d2: 5x + 2y – 14 = 0. A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau. Đáp án: B.
Câu 29. Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng (a):x + 3y – 1 = 0; (b):x – 3y – 5 = 0 và vuông góc với đường thẳng (c):2x – y + 7 = 0. A. 3x + 6y – 5 = 0. B. 6x + 12y – 5 = 0. C. 6x + 12y + 7 = 0 . D. x + 2y + 10 = 0. Đáp án: A.
