Bài toán tính góc giữa đường thẳng và mặt phẳng là một dạng toán học thuộc chương trình Toán 11. Dưới đây là bài viết về Phương pháp tính góc giữa đường thẳng và mặt phẳng siêu hay, mời các bạn học sinh cùng theo dõi.
Mục lục bài viết
1. Phương pháp tính góc giữa đường thẳng và mặt phẳng dễ hiểu:
Để xác định góc giữa đường thẳng a và mặt phẳng (α) ta thực hiện theo các bước sau:

+ Bước 1: Tìm giao điểm O của đường thẳng a và (α)
+ Bước 2: Dựng hình chiếu A’ của một điểm A ∈ a xuống (α)
+ Bước 3: Góc ∠AOA’ = φ chính là góc giữa đường thẳng a và (α)
Lưu ý:
– Để dựng hình chiếu A’ của điểm A trên (α) ta chọn một đường thẳng b ⊥ (α) khi đó AA’ // b.
– Để tính góc φ ta sử dụng hệ thức lượng trong tam giác vuông OAA’.
2. Ví dụ minh họa về cách tính góc giữa đường thẳng và mặt phẳng:
Ví dụ 1: Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
A. Góc giữa AC và (BCD) là góc ACB
B. Góc giữa AD và (ABC) là góc ADB
C. Góc giữa AC và (ABD) là góc ACB
D. Góc giữa CD và (ABD) là góc CBD
Hướng dẫn giải

Chọn A.

Ví dụ 2: Cho tam giác ABC vuông cân tại A và BC = a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho SA = (√6)a/2 . Tính số đo góc giữa đường thẳng SA và (ABC) .
A. 30° B. 45° C. 60° D. 90°
Hướng dẫn giải

Chọn D
Từ giả thiết suy ra:
SA ⊥ (ABC) ⇒ (SA, (ABC)) = 90°
Ví dụ 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).
A. 30° B. 45° C. 60° D. 75°
Hướng dẫn giải

Chọn C
Gọi H là trung điểm của BC suy ra
AH = BH = CH = (1/2)BC = a/2

Ví dụ 4: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD) . Biết SA = a(√6)/3. Tính góc giữa SC và (ABCD) .
A. 30° B. 45° C. 60° D.90°
Hướng dẫn giải

Chọn A

Ví dụ 5: Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)
A. 60° B.90° C. 45° D. 30°
Hướng dẫn giải
Do H là hình chiếu của S lên mặt phẳng ( ABC) nên SH ⊥ (ABC)
Vậy AH là hình chiếu của SH lên mp(ABC)
⇒ (SA, (ABC)) = (SA, AH) = ∠ SAH
Ta có: SH ⊥ (ABC) ⇒ SH ⊥ AH
Mà: ΔABC = ΔSBC ⇒ SH = AH
Vậy tam giác SAH vuông cân tại H ⇒ SAH = 45°
Chọn C
Ví dụ 6: Cho hình thoi ABCD có tâm O, AC = 2a ; BD = 2AC . Lấy điểm S không thuộc (ABCD) sao cho SO ⊥ (ABCD) . Biết tan(SBO) = 1/2. Tính số đo của góc giữa SC và ( ABCD)
A. 30° B.45° C. 60° D. 90°
Hướng dẫn giải

Chọn B

3. Bài tập vận dụng kèm lời giải:
Câu 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điể BC . Biết SB = a. Tính số đo của góc giữa SA và (ABC)
A. 30° B.45° C. 60° D. 75°
Lời giải:

Gọi M là trung điểm BC.
Tam giác ABC vuông đường trung tuyến AM nên:
AM = BM = a/2, SB = a
Có SM ⊥ (ABC) nên AM là hình chiếu của SA lên mp(ABC)
⇒ ( SA,(ABC)) = (SA, AM) = ∠SAM
Áp dụng định lý Pytago

Xét tam giác SAM có
tan(SAM) = SM/AM = √3 ⇒ ∠SAM = 60°
Vậy chọn C
Câu 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy và SA = a. Góc giữa đường thẳng SC và mặt phẳng (SAB) là α, khi đó tanα nhận giá trị nào trong các giá trị sau?
Lời giải:


Câu 3: Cho hình chóp S. ABC có SA ⊥ (ABC) và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm tam giác ABC và tam giác SBC. Số đo góc tạo bởi SC và (BHK) là:
A. 45° B. 120° C. 90° D. 65°
Lời giải:
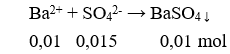
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với mp( ABCD). Gọi α là góc giữa BD và mp(SAD) . Chọn khẳng định đúng trong các khẳng định sau?
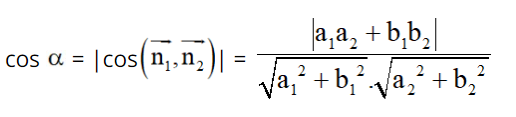
Lời giải:
Gọi I là trung điểm AS.
+ Ta chứng minh AD ⊥ (SAB):
Do AD ⊥ AB và AD ⊥ SH ( vì SH ⊥ (ABCD)
⇒ AD ⊥ (SAB) nên AD ⊥ BI.
Lại có: BI ⊥ SA
⇒ BI ⊥ (SAD)
⇒ góc giữa BD và (SAD) là góc ∠IDB
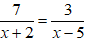
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = a√6. Gọi α là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau ?
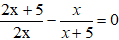
Lời giải:
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên (ABCD)
⇒ Góc giữa giữa SC và mp(ABCD) bằng góc giữa SC và AC
⇒ α = ∠SCA
Xét tam giác SAC vuông tại A có:

Chọn D
Câu 6: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi α là góc giữa AC’ và mp(A’BCD’). Chọn khẳng định đúng trong các khẳng định sau?
Lời giải:
Câu 6: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Trung tuyến SI của tam giác đều SAB vuông góc với đáy (ABCD) của hình chóp. Chứng minh hai đường thẳng SC và SD tạo với mặt phẳng (SAB) hai góc bằng nhau. Tính góc giữa đường thẳng CM và mặt phẳng (SAB), trong đó M là trung điểm SD.
Lời giải: Hai đường thẳng SC và SD cùng tạo với mặt phẳng (SAB) góc 45∘. Hình chiếu của điểm C lên mặt phẳng (SAB) là B. Hình chiếu của điểm M lên mặt phẳng (SAB) là trung điểm N của SA. Góc giữa đường thẳng CM và mặt phẳng (SAB) bằng 30∘
Câu 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tâm O và SO vuông góc với đáy. Gọi M,N lần lượt là trung điểm của các cạnh SA và BC. Biết góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng 60∘. Tính độ dài MN và SO. Tính góc giữa đường thẳng MN và mặt phẳng (SBD).
Lời giải: Gọi H là trung điểm của AO thì MH song song với SO nên H là hình chóp vuông góc của M lên mặt phẳng (ABCD)… Đáp số MN=a10√2,SO=a30√2;sin(MN,(SBD))=15√
Câu 8: Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
1. Góc giữa AC và (BCD) là góc ACB
2. Góc giữa AD và (ABC) là góc ADB
3. Góc giữa AC và (ABD) là góc ACB
4. Góc giữa CD và (ABD) là góc CBD
Hướng dẫn giải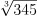
Chọn đáp án A.
Câu 9: Cho tam giác ABC vuông cân tại A và BC = a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho SA = √6 a/2 . Tính số đo góc giữa đường thẳng SA và (ABC) .
A. 30° B. 45° C. 60° D. 90°
Tam giác ABC vuông cân tại A
Từ giả thiết suy ra:
SA ⊥ (ABC) ⇒ (SA, (ABC)) = 90°
Chọn đáp án D.
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).
A. 30° B. 45° C. 60° D. 75°
Hướng dẫn giải

Câu 11: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD) . Biết SA = a(√6)/3. Tính góc giữa SC và (ABCD) .
A. 30° B. 45° C. 60° D.90°
Hướng dẫn giải