Bài viết Cách tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ với phương pháp giải chi tiết giúp các bạn học sinh ôn tập, biết cách làm bài tập Cách tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ. Mời các bạn học sinh tham khảo trong bài viết dưới đây
Mục lục bài viết
1. Cách tính độ dài vecto đơn giản, chính xác nhất:
Độ dài vecto:
– Định nghĩa: mỗi vecto đều có một độ dài đó bằng là khoảng cách giữa hai điểm đầu và điểm cuối của vecto đó. Độ dài của veco a được ký hiệu là: ![]()
Do đó đối với các vecto ![]() ,… thì ta có:
,… thì ta có:
![]() = AB = BA
= AB = BA
![]() = PQ = QP
= PQ = QP
– Phương pháp: muốn tính độ dài vecto ta tính độ dài cách giữa điểm đầu và điểm cuối của vecto:
– Trong toạ độ : Cho ![]() ( a1; a2)
( a1; a2)
Độ dài vecto: ![]() là
là ![]() =
= ![]()
Khoảng cách giữa hai điểm trong hệ toạ độ:
Áp dụng công thức:
Trong mặt phẳng toạ độ thì khoảng cách giữa hai điểm M (xM; yM) và N(xN; yN) là:
MN = ![]() =
= ![]()
2. Ứng dụng của công thức tính độ dài của vectơ trong thực tế:
Công thức tính độ dài của vectơ là một công thức quan trọng trong toán học và có ứng dụng rộng rãi trong thực tế.
Ứng dụng đầu tiên của công thức tính độ dài của vectơ là trong hình học. Khi chúng ta biết tọa độ hai điểm trên mặt phẳng, ta có thể sử dụng công thức để tính khoảng cách giữa hai điểm đó. Điều này rất hữu ích trong thiết kế hình học, định vị GPS và bản đồ.
Ứng dụng thứ hai của công thức tính độ dài của vectơ là trong vật lý. Trong cơ học, chúng ta có thể sử dụng công thức này để tính độ dài của các vật thể di chuyển trong không gian. Ví dụ, trong động học chuyển động, ta có thể tính được khoảng cách mà một vật di chuyển trong quá trình chuyển động.
Ngoài ra, công thức tính độ dài của vectơ cũng được áp dụng trong các lĩnh vực khác như điện tử, tin học và kỹ thuật. Trong viễn thông, công thức này được sử dụng để tính độ dài của tín hiệu truyền thông. Trong tin học, công thức này được sử dụng để tính độ dài của chuỗi ký tự hoặc mã hóa. Trong kỹ thuật, công thức này có thể được sử dụng để tính độ dài của các vật liệu, đo đạc và xác định vị trí.
Tóm lại, công thức tính độ dài của vectơ có nhiều ứng dụng trong thực tế, từ hình học đến vật lý, từ điện tử đến kỹ thuật. Hiểu và áp dụng công thức này giúp chúng ta giải quyết nhiều vấn đề thực tế một cách nhanh chóng và chính xác.
3. Các dạng bài tính độ dài vecto:
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ ![]() =(4;1) và
=(4;1) và ![]() =(1;4). Tính độ dài vectơ
=(1;4). Tính độ dài vectơ ![]()
Hướng dẫn giải:
Ta có:
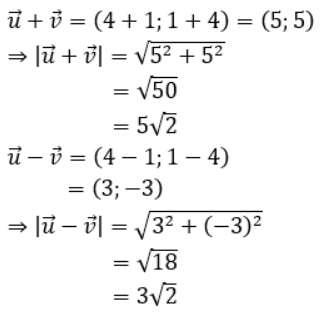
Ví dụ 2: Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M(1; -2) và N (-3; 4).

Hướng dẫn giải:

Đáp án D
Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4), B(3; 2), C(5; 4). Chu vi P của tam giác đã cho.
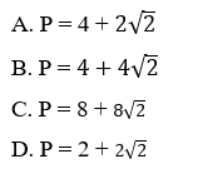
Hướng dẫn giải:

Đáp án B
Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-1; 1), B(0; 2), C(3; 1) và D(0; -2). Khẳng định nào sau đây là đúng?
A. Tứ giác ABCD là hình bình hành
B. Tứ giác ABCD là hình thoi
C. Tứ giác ABCD là hình thang cân
D. Tứ giác ABCD không nội tiếp được đường tròn
Hướng dẫn giải:

Từ (1) và (2) suy ra ABCD là hình thang cân (hình thang có hai đường chéo bằng nhau là hình thang cân).
Đáp án C
Ví dụ 5: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;3) và B(4;2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B.
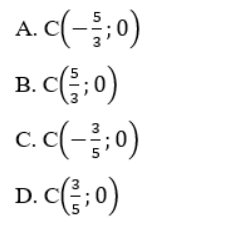
Hướng dẫn giải:

Đáp án B
3. Bài tập tự luyện tập:
Câu 1: Trong mặt phẳng toạ độ Oxy cho hai vecto ta có vecto v = ( 4; 1) và vecto u = (1 ; 4). Tính độ dài vecto u + vecto v ; vecto u + vecto v
Câu 2: Trong mặt phẳng toạ độ Oxy có hai điểm M ( 1; -2) và N ( -3 ; 4) , hãy tính khoảng cách giữa hai điểm
A. MN = 4
B. MN = 6
C. MN = 3 căn 6
D. MN = 2 căn 13
Câu 3: Trong mặt phẳng toạ độ Oxy cho tam giác ABC có A (1; 4) ; B (3 ; 2) ; C ( 5 ; 4). Tính chu vi của tam giác đã cho
A. P = 4 + 2 căn 2
B. P = 4 + 4 căn 2
C. P = 8 + 8 căn 2
D. P = 2 + 2 căn 2
Câu 4: Trong mặt phẳng toạ độ Oxy cho hai điểm A(1 ; 3) và B ( 4;2 ). Tìm toạ độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B
Câu 5: Trong mặt phẳng toạ độ Oxy cho bốn điểm A ( -1 ; 1) , B ( 0;2) , C (3 ; 1) và D (0; -2). Khẳng định nào sau đây là đúng?
A. tứ giác ABCD là hình bình hành
B. tứ giác ABCD là hình thoi
C. tứ giác ABCD là hình thang cân
D. tứ giác ABCD không nội tiếp đường tròn
Câu 6: TRong mặt phẳng toạ độ Oxy cho hai điểm A (1;3) và B (4;2). Tìm toạ độ điểm C thuộc trục hoàng sao cho C cách đều hai điểm A và B
A. C (-5/3; 0)
B. C (5/3; 0)
C. ( -3/5 ; 0)
D. (3/5 ; 0)
Câu 7: Cho hình bình hành ABCD có tâm O. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA.
a. Các cặp vecto sau đây có cùng phương không: vecto AB và vecto MB ; vecto QM và vecto BD ; vecto AD và vecto MC
b. tìm các vecto cùng hướng, ngược hướng với vecto MN
c. tìm các vecto lần lượt bằng với các vecto OB
Câu 8: Cho tam giác ABC . Hãy dựng các điểm M, N sao cho vecto AM = vecto BC, vecto An = vecto CB. Nhận xét gì về hai vecto AM và vecto AN và 3 điểm A, M , N
Câu 9: Cho hình thang ABCD có đáy là AB và CD, AB = 2 CD, từu C vẽ vecto CI = vecto DA
a. chứng minh I là trung điểm của AB và vecto AI = vecto CB
b. chứng minh vecto AI = vecto IB = vecto DC
Câu 10: cho tam giác đều ABC có cạnh AB = a , kẻ đường cao AH
a. gọi E, F là hai điểm trên cạnh BC sao cho BE = FE = FC tính tổng vecto u = vecto AB + vecto EA + vecto AC + vecto FA
b. Xác định vecto AH + BH . Tính độ dài vecto AH + vecto BH theo a
Câu 11: Cho tứ giác ABCD , gọi E và F lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của EF. M là điểm tuỳ ý. Hãy chúng minh
A. vecto AD + vecto BC = 2 vecto EF
B. vecto OA + vecto OB + vecto OC + vecto OD = vecto 0
C. vecto AB + vecto AC + vecto AD = 4 vecto AO
D. vecto MA + vecto MB + vecto MC + vecto MD = 4 vecto MO
Câu 12: cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O.
a. chứng minh tứ giác BHCD là hình bình hành, suy ra vecto HA + vecto HB + vecto HC = 2 vecto HO
b. chứng minh vecto OA + vecto OB + vecto OC = vecto OH
c. Gọi G là trọng tâm của tam giác ABC. chứng minh vecto OH = 3 vecto OG. từ đó có kết luận gì về ba điểm O, H, G
Câu 13: cho hình thoi ABCD tâm O, cạnh bằng 4a, BD = 4a, gọi I là trung điểm của OC
a. tính độ dài các vecto BO + vecto BC – 2 vecto CI , vecto AB – vecto BC
b. tìm M trên CD sao cho vecto MO + vecto MC + 2 vecto IA có độ dài ngắn nhất
Câu 14: cho tam giác ABC
a. xác định điểm M sao cho vecto AM = vecto BC
b. xác định điểm N sao cho vecto BN = -2 vecto AC
Câu 15: cho tam giác ABC, gọi I là điểm trên cạnh BC sao cho 2 CI = 3 BI. Gọi F là điểm trên cạnh BC kéo dài sao cho 5 FB = 2 FC
a. phân tích vecto AI, vecto AF theo vecto AB, vecto AC
b. gọi G là trọng tâm của tam giác ABC. tính độ dài của vecto AG theo vecto AI và vecto AF




