Có nhiều dạng bài tìm tập xác định của hàm số lượng giác và mỗi dạng bài tập lại có phương pháp giải khác nhau. Trong bài viết dưới đây hãy cùng chúng tôi tìm hiểu cách tìm tập xác định của hàm số lượng giác chuẩn nhất.
Mục lục bài viết
1. Cách tìm tập xác định của hàm số lượng giác chuẩn nhất:
Dưới đây là một số dạng bài tập và phương pháp giải trong hàm số lượng giác:
Dạng 1. Tìm tập xác định của hàm số lượng giác:
Phương pháp giải:
Để tìm tập xác định của hàm số lượng giác, chúng ta có một số phương pháp sau đây:
– Phương pháp xác định tập xác định, tập giá trị của hàm số lượng giác khi g(x) ≠ 0.
– Phương pháp xác định tập xác định, tập giá trị của hàm số lượng giác khi f(x) ≥ 0.
– Phương pháp xác định tập xác định, tập giá trị của hàm số lượng giác khi g(x) > 0.
Điều kiện xác định cho y = tan[u(x)] là u(x) ≠ Phương pháp xác định, tập giá trị của hàm số lượng giác + kπ, với k ∈ Z.
Điều kiện xác định cho y = cot[u(x)] là u(x) ≠ kπ, với k ∈ Z.
Điều kiện xác định cho sin x khác 0 là x khác kπ, với k ∈ Z.
Điều kiện xác định cho cos x khác 0 là x khác Phương pháp xác định, tập giá trị của hàm số lượng giác + kπ, với k ∈ Z.
Vậy, tập xác định của hàm số lượng giác được xác định bằng phương pháp tìm tập xác định, tập giá trị của hàm số lượng giác.
Bên cạnh đó, chúng ta cũng có thể sử dụng phương pháp khác như tìm điểm phân giác của hàm số lượng giác để xác định tập xác định. Điểm phân giác là các giá trị của biến số mà hàm số không xác định tại đó và tạo ra “nhảy” giá trị của hàm số.
Dạng 2. Tìm tập giá trị của hàm số lượng giác:
Phương pháp giải:
Để tìm tập giá trị của hàm số lượng giác, chúng ta có thể sử dụng tính bị chặn của hàm số lượng giác. Tập giá trị của hàm số lượng giác là tập các giá trị mà hàm số có thể nhận được. Điều này có thể được xác định bằng cách xem xét các giới hạn của hàm số.
Đặc biệt, khi giới hạn của hàm số tiến đến ±∞, tập giá trị của hàm số sẽ bao gồm tất cả các giá trị thực.
Để tìm tập giá trị của hàm số lượng giác, chúng ta cũng có thể sử dụng phương pháp khác như vẽ đồ thị của hàm số và xác định các điểm cực trị và điểm yên ngựa của hàm số. Các điểm cực trị và điểm yên ngựa sẽ giúp chúng ta xác định các giá trị cao nhất, thấp nhất và các giá trị địa phương của hàm số.
Dạng 3. Tìm m để hàm số lượng giác có tập xác định là R:
Phương pháp giải:
Để hàm số lượng giác có tập xác định là R, chúng ta có một số phương pháp sau đây:
– Nếu m ≥ f(x) ∀x ∈ [a,b], thì m ≥ phương pháp tìm tập xác định, tập giá trị của hàm số lượng giác.
– Nếu m > f(x) ∀x ∈ [a,b], thì m > phương pháp tìm tập xác định, tập giá trị của hàm số lượng giác.
– Nếu m ≤ f(x) ∀x ∈ [a,b], thì m ≤ phương pháp tìm tập xác định, tập giá trị của hàm số lượng giác.
– Nếu m < f(x) ∀x ∈ [a,b], thì m < phương pháp tìm tập xác định, tập giá trị của hàm số lượng giác.
Ngoài ra, chúng ta cũng có thể sử dụng đồ thị hàm số để xác định tập giá trị của hàm số lượng giác. Bằng cách vẽ đồ thị và xem xét hình dạng của hàm số, chúng ta có thể xác định được các giá trị mà hàm số có thể nhận được.
Hy vọng những thông tin trên giúp bạn hiểu rõ hơn về các dạng bài tập và phương pháp giải trong hàm số lượng giác. Hãy áp dụng những kiến thức này vào việc giải quyết các bài tập của bạn. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại hỏi để được giải đáp thêm. Chúc bạn thành công và tiến bộ trong học tập!
2. Mẹo làm bài tập tìm tập xác định của hàm số lượng giác chính xác:
Dưới đây là một số mẹo khi làm bài tập tìm tập xác định của hàm số lượng giác:
– Đầu tiên, hãy đọc đề bài một cách kỹ lưỡng và xác định rõ hàm số lượng giác mà bạn đang cần tìm tập xác định.
– Tiếp theo, hãy xác định các giới hạn và điều kiện để hàm số lượng giác tồn tại. Bạn cần tìm hiểu về các quy tắc và ràng buộc liên quan đến hàm số lượng giác, chẳng hạn như giới hạn của các hàm số liên quan và các điều kiện tồn tại của chúng.
– Sau đó, hãy giải phương trình hoặc bất phương trình để tìm tập xác định của hàm số lượng giác. Điều này có thể yêu cầu bạn áp dụng các phép toán và quy tắc chuyển đổi để giải quyết các phương trình phức tạp hoặc bất phương trình.
– Cuối cùng, hãy kiểm tra kết quả và đảm bảo rằng tập xác định mà bạn đã tìm được phù hợp với hàm số lượng giác. Điều này có thể bao gồm việc kiểm tra lại các ràng buộc và sử dụng các kiến thức về biến đổi hàm số để đảm bảo tính hợp lệ của tập xác định.
Hy vọng những mẹo này sẽ giúp bạn khi làm bài tập về tìm tập xác định của hàm số lượng giác.
3. Bài tập vận dụng liên quan:
Bài 1: Cho hàm số y = tanx – cotx. Khoảng mà hàm số xác định là:

Đáp án: D
Bài 2: Hãy chỉ ra hàm số chẵn trong các hàm số sau:
A.y = sinx
B.y= sinx + cotx
C.y= sin(π/2-x)
D.y= sinx.cos2x
Đáp án: C
Bài 3: Hãy chỉ ra hàm số lẻ trong các hàm số sau:
A.y= cos2x.cos(π/2-x)
B.y= sin2xcosx
C.y= sinx – cosx
D.y= xsinx
Đáp án: A
Bài 4: Hàm số nào sau đây không có tính chẵn, lẻ?
A.y= cos2xcos(π/2-x)
B.y= sin2x.cosx
C.y= sinx – cosx
D.y= x.sinx
Lời giải:
Đáp án: C
Bài 5: Hàm số y = tanx xác định trong tập nào sau đây?

Đáp án: A
Bài 6: Cho hàm số y= 2sin(x/2), hãy chỉ ra mệnh đề sai trong bốn mệnh đề sau:
A. Hàm số đã cho là hàm số lẻ.
B. Hàm số đã cho có giá trị lớn nhất bằng 2.
C. Hàm số đã cho có chu kì 4π.
D. Trong ba mệnh đề trên có ít nhất một mệnh đề sai.
Lời giải:
Đáp án: A
Bài 7: Hãy chỉ ra hàm số tuần hoàn trong các hàm số sau:

Đáp án: B
Bài 8: Hàm số sau có tập xác định là:
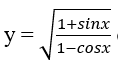
A.R\{kπ,k ∈ Z}
B.R
C.R\{k2π,k ∈ Z}
D.R\{π/2+k2π, k ∈ Z}
Đáp án: C
Bài 9: Chu kì của hàm số y = tan (x/2) là:
A.2π
B.4π
C.π
D.π/2
Đáp án: A
Bài 10: Tìm tập xác định D của hàm số y = (sinx + 2)/ (sinx.cos2x)

Đáp án: A
Bài 11: Chu kì của hàm số y = sin5x là:
A.2π
B.5π
C.10π
D.2π/5
Đáp án: D
Bài 12: Chu kì của hàm số y = sin (x/3) là
A.2π
B.6π
C.π/3
D. 2π/3
Đáp án: B
Bài 13: Hàm số sau có tập xác định:
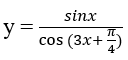
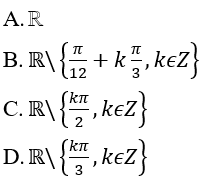
Đáp án: B
Bài 14: Tìm tập giá trị của hàm số sau:
![]()
A. D = [0,+∞) B. D = ∅
C. D = R D. D = [1,√3]
Đáp án: D
Bài 15: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. y = cosx + (sinx)2
B. y = sin x + cosx
C. y = -cosx
D. y = sinx.cos3x
Đáp án: D
Bài 16: Chu kì của hàm số y = cos(x/2) + sinx là:
A.0
B.2π
C.4π
D.6π
Đáp án: C
Bài 17: Tập xác định D của hàm số sau là
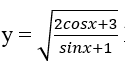

Đáp án: B
Bài 18: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sinx
B. y = cosx
C. y = tan x
D. y = cotx
Đáp án: B
Bài 19: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
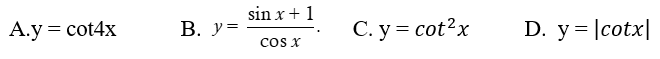
Đáp án: A
Bài 20: Giá trị nhỏ nhất của hàm số y = 2 + sinxcosx là:
A.1
B.3/2
C.2
D.Một số khác
Đáp án: B
Bài 21: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?

Đáp án: B
Bài 22: Giá trị lớn nhất của hàm số y = 3sinx + 4cosx là:
A.3
B.4
C.5
D.7
Đáp án: C
Bài 23: Tìm tập giá trị của hàm số sau: y = 2017/sinx
A. D = R\ {0}
B. D = [-2017,2017]
C. D = R
D. D = (-∞,-2017] ∪ [2017,+∞)
Đáp án: D
Bài 24: Hàm số y = 1/(sinx-cosx) có tập xác định là:
A. ℝ\{kπ,k ∈ Z}
B. ℝ\{k2π,k ∈ Z}
C. ℝ\{π/2+kπ,k ∈ Z}
D. ℝ\{π/4+kπ,k ∈ Z}
Đáp án: D
Bài 25: Hàm số sau có tập xác định là:
![]()
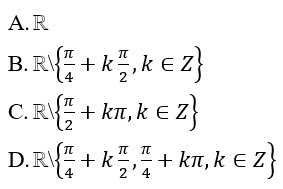
Đáp án: B
Bài 26: Tập xác định của hàm số y = sin√x là:
A.ℝ
B.ℝ\{0}
C.[0;+∞)
D.(0;- ∞)
Đáp án: C
Bài 27: Hàm số y = 2sinxcosx + cos2x có giá trị lớn nhất là
A.3
B.2√2
C.2
D.√2
Đáp án: D
Bài 28: Hàm số y = 2cos2x – 1 là hàm tuần hoàn với chu kì:
A.T = π.
B.T = 2π.
C.T = π2
D.T = π/2.
Đáp án: A
Bài 29: Tìm tập xác định của hàm số sau: y = 2017/sinx
A. D = R
B. D = R\ {kπ, k ∈ Z}
C. D = R\{0}
D. D = R\ {π/2+kπ, k ∈ Z}
Đáp án: B




