Với nội dung Cách tìm tập xác định của hàm số kèm Bài tập vận dụng sau đây sẽ giúp học sinh nắm vững lý thuyết, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 10. Cùng tham khảo nhé.
Mục lục bài viết
1. Cách tìm tập xác định của hàm số:
*Phương pháp giải:
Tập xác định của hàm số y = f(x) là tập các giá trị của x sao cho biểu thức f(x) có nghĩa. Như vậy, để tìm tập xác định chúng ta cần tìm điều kiện xác định của biểu thức f(x). Biểu thức f(x) thường là một số dạng sau:
+) f(x)= 
. Khi đó f(x) có nghĩa khi và chỉ khi B(x)#0 .
+) f(x)=
. Khi đó f(x) có nghĩa khi và chỉ khi A(x)
0 .
+) f(x)=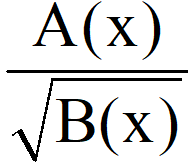 
. Khi đó f(x) có nghĩa khi và chỉ khi B(x) > 0.
+) f(x)=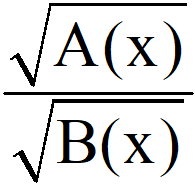
. Khi đó f(x) có nghĩa khi và chỉ khi A(x) và B(x) > 0.
*Ví dụ minh họa:
Ví dụ 1: Tìm tập xác định của các hàm số sau:
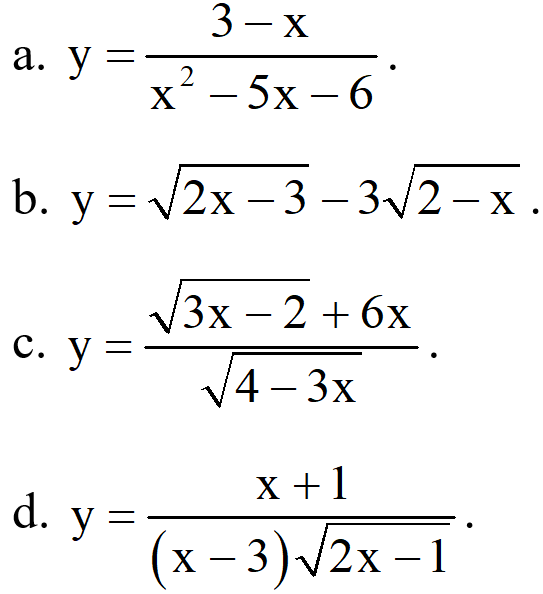
Lời giải:
a. Điều kiện xác định của hàm số là: x2 – 5x – 6#0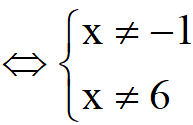 
.
Vậy tập xác định của hàm số đã cho là: D= R{-1;6}.
b. Điều kiện xác định của hàm số là:
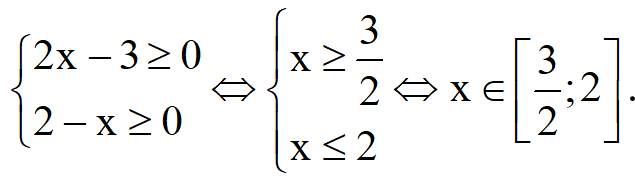
Vậy tập xác định của hàm số đã cho là: D=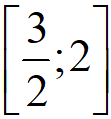 
c. Điều kiện xác định của hàm số là: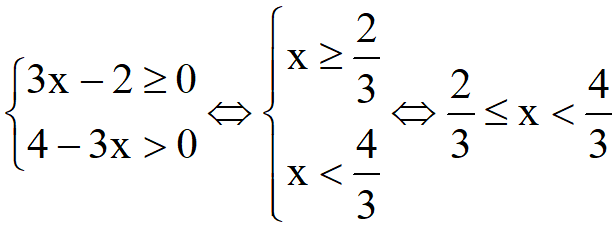 
Vậy tập xác định của hàm số đã cho là D= 
.
d. Điều kiện xác định của hàm số là: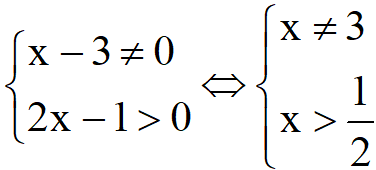
Vậy tập xác định của hàm số đã cho là: D=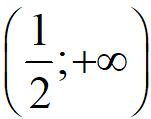 
{3}.
Ví dụ 2: Tìm tập hợp tất cả các giá trị của m để:
a. y=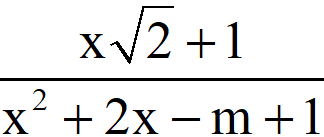 
có tập xác định là R .
b. y= (x-2) 
xác định trên khoảng (1:+ 
)
Lời giải:
a. Hàm số có tập xác định là R khi
x2 + 2x – m + 1#0 , 
x
Phương trình bậc hai x2 + 2x – m + 1 = 0 vô nghiệm
= 22 – 4(-m+1) = 4 + 4m – 4 < 0 m<0
Vậy với m < 0 thì hàm số đã cho có tập xác định là R
b. Điều kiện xác định của hàm số là: 3x – m -1 0
.
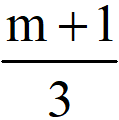Suy ra tập xác định của hàm số là: D=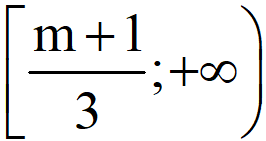 
Để hàm số xác định trên (1;+ ) thì
(1;+ ) 1 m+1
3 
m 2
Vậy với m 2 thì hàm số đã cho xác định trên khoảng (1;+ ).
2. Bài tập tự luận:
Câu 1: Tìm tất cả các giá trị của tham số m để hàm số y= 
xác định trên đoạn [3; 5].
Lời giải:
Điều kiện xác định của hàm số là x – 2m – 1#0 x#2m+1
Hàm số xác định trên đoạn [3; 5] 2m+1 
[3;5] 
.
Vậy với m < 1 hoặc m > 2 thì hàm số đã cho xác định trên đoạn [3; 5]
Câu 2: Có bao nhiêu giá trị nguyên của x thuộc tập xác định của hàm số 
?
Lời giải:
Tập xác định: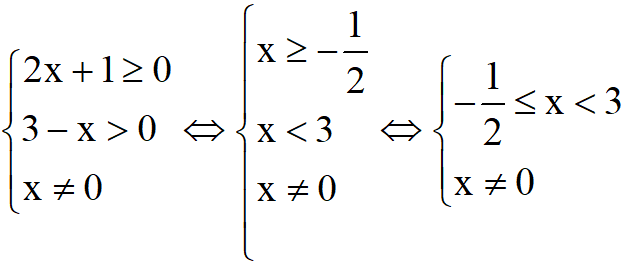
Do x nguyên nên x 
{1;2}
Câu 3: Xét tính chẵn, lẻ của hàm số: y = f(x) =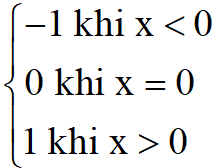
Hướng dẫn:
Tập xác định: D=(- ;0)
(0:+)=R
+ Khi x < 0 thì -x > 0 
f(-x) = 1 = -f(x).
+ Khi x > 0 thì -x < 0 f(-x) = -1 = -f(x) .
+ Khi x=0 thì f(-0) = f(0) = 0= -f(0).
Suy ra với mọi x R thì f(-x) = -f(x).
Vậy hàm số đã cho là hàm số lẻ.
Câu 4: Cho hàm số f(x)=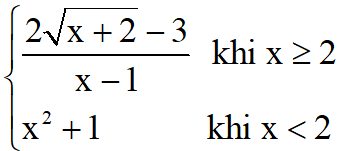 
.Tính f(-2)+f(2).
Lời giải:
Ta có: f(2)=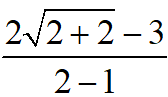
=1, f(-2) = (-2)2 +1 =5
Suy ra: f(-2) + f(2) = 6
Câu 5: Xét tính đơn điệu của hàm số y=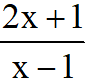
.
Lời giải:
Tập xác định: D=R{1}.
+) Lấy x1 ; x2 (-
;1) sao cho x1 < x2. Xét:
y1-y2=
=
Với x1 ; x2 
(- ;1) và x1 < x2, ta có:
x1 – x2 >0; x1 – 1<0; x2 – 1<0 
y1-y2 >0 
y1>y2
Do đó hàm số nghịch biến trên (- ;1) (1)
+) Lấy x1 ; x2 (1;+ ) sao cho x1 < x2 .Xét:
y1-y2= 
Với x1 ; x2 (1;+ ) và x1 < x2, ta có:
x1 – x2 >0; x1 – 1>0; x2 – 1>0 y1-y2 >0 y1>y2
Do đó hàm số nghịch biến trên (1;+ ) (2)
Từ (1) và (2) suy ra hàm số nghịch biến trên D.
Câu 6: Tìm tập xác định của hàm số: y= 
?
Lời giải:
Hàm số y= xác định khi và chỉ khi
0 (luôn đúng x R)
Vậy tập xác định của hàm số là R.
Câu 7: Xét tính chẵn, lẻ của hàm số y=f(x) = 3×4 – 4×2 + 3 .
Lời giải:
Tập xác định D=R .
Ta có
Do đó hàm số y = f(x) là hàm số chẵn.
Câu 8: Cho hàm số: f(x)= 
. Tính f(0), f(2). f(-2).
Lời giải:
Ta có: f(0)=
=0, f(2)= 
=
(do x 
0 ) và f(-2)= 
= 
(do x < 0).
Câu 9: Tìm tập xác định của hàm số y= 
Lời giải:
Hàm số đã cho xác định khi 
Vậy tập xác định của hàm số là D=[-1;+ 
){2}.
Câu 10: Tìm m để hàm số y= 
xác định trên R.
Hướng dẫn:
Hàm số y=
xác định trên R khi phương trình x2 – 2x -3 – m =0 vô nghiệm
Hay 
=m+4<0
m < -4.
3. Bài tập trắc nghiệm:
Câu 1: Tập xác định của hàm số y= x4 – 2018×2 – 2019 là:
A. (-1+ 
).
B. (- ;0).
C. (0;+ ).
D. (- ;+ ) .
Lời giải:
Chọn D.
Hàm số là hàm đa thức nên xác định với mọi số thực x.
Câu 2: Tập xác định của hàm số y= 
-x là:
A. (-
;4].
B. [4;+ ).
C. [0; 4].
D. [0;+ ).
Hướng dẫn :
Chọn A.
Điều kiện xác định của hàm số là 8-2x
0
x 
4, nên tập xác định là (- ;4).
Câu 3: Cho hàm số y=x2. Chọn mệnh đề đúng.
A. Hàm số trên là hàm chẵn.
B. Hàm số trên vừa chẵn vừa lẻ.
C. Hàm số trên là hàm số lẻ.
D. Hàm số trên không chẵn không lẻ.
Lời giải:
Chọn A.
Đặt f(x)=x2.
Tập xác định D=R.
Ta có 
x 
D
-x D và f(-x) = (-x)2 = x2 = f(x) .
Vậy hàm số trên là hàm số chẵn.
Câu 4: Cho hàm số y=f(x)=
Mệnh đề nào sau đây sai?
A. Hàm số y = f(x) có tập xác định là R .
B. Đồ thị hàm số y = f(x) nhận trục tung làm trục đối xứng.
C. Hàm số y = f(x) là hàm số chẵn.
D. Đồ thị hàm số y = f(x) nhận gốc tọa độ làm tâm đối xứng.
Lời giải:
Chọn D.
Tập xác định của hàm số là R.
x Rthì -x
R, ta có:
f(-x) =
=f(x)
Hàm số đã cho là hàm số chẵn, đồ thị nhận trục tung làm trục đối xứng. Do vậy các phương án A, B, C đều đúng. Đáp án D sai.
Câu 5: Chọn khẳng định đúng?
A. Hàm số y = f(x) được gọi là nghịch biến trên K nếu
x1;x2 
K, 
x1
B. Hàm số y = f(x) được gọi là đồng biến trên K nếu
x1;x2 K, x1 f(x1) 
f(x2)
C. Hàm số y = f(x) được gọi là đồng biến trên K nếu
x1;x2 K, x1 f(x1)>f(x2)
D. Hàm số y = f(x) được gọi là đồng biến trên K nếu
x1;x2 K, x1f(x1)
Lời giải:
Chọn D.
Lí thuyết định nghĩa hàm số đồng biến, nghịch biến.
Câu 6: Xét sự biến thiên của hàm số f(x)=
trên khoảng (0;+ 
) . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (0;+ ).
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng (0;+ ).
C. Hàm số đồng biến trên khoảng (0;+ ).
D. Hàm số không đồng biến, không nghịch biến trên khoảng (0;+ ).
Lời giải:
Chọn A.
x1;x2 (0;+ ), x1#x2, ta có:
f(x2)-f(x1)= 
Vậy hàm số nghịch biến trên khoảng (0;+ ).
Câu 7: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng (0; 3).
B. Hàm số đồng biến trên khoảng (- ;1).
C. Hàm số nghịch biến trên khoảng (0; 2).
D. Hàm số đồng biến trên khoảng (- ;3).
Lời giải:
Chọn C.
Trên khoảng (0; 2), đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Câu 8: Cho hàm số y= x3 – 3x + 2. Điểm nào sau đây thuộc đồ thị hàm số đã cho?
A. (-2; 0).
B. (1; 1).
C. (-2; -12).
D. (1; -1).
Lời giải:
Chọn A.
Thay tọa độ điểm vào hàm số ta thấy chỉ có điểm (-2; 0) thỏa mãn.
