Mục lục bài viết
1. Cách tìm số phức liên hợp cực hay, chi tiết:
Cho số phức z = a + bi. Ta gọi số phức liên hợp của z là ![]() = a – bi.
= a – bi.
Kết quả: ∀ z ∈ C ta có:

Z là số thực khi z = ![]()
Z là số thuần ảo khi z = –![]()
Ví dụ minh họa
Ví dụ 1: Cho số phức z = 1 + 3i Tìm số phức ![]()
A. ![]() = 1 – 3i. B.
= 1 – 3i. B. ![]() = 3 – i. C.
= 3 – i. C. ![]() = 3 + i. D.
= 3 + i. D.![]() = 1 + 3i.
= 1 + 3i.
Hướng dẫn:
Với z = 1 + 3i thì ![]() = 1 – 3i
= 1 – 3i
Chọn A.
Ví dụ 2: Cho số phức z = -2 – 5i Tìm phần thực a và phần ảo b của số phức ![]() .
.
A. a = -2 ; b = 5 B. a = -2; b = -5 C. a = -5; b = 2 D. a = -5; b = -2
Hướng dẫn:
z = a + bi => ![]() = a – bi
= a – bi
Nên ![]() = -2 + 5i vậy. Phần thực bằng a = -2 và phần ảo b = 5
= -2 + 5i vậy. Phần thực bằng a = -2 và phần ảo b = 5
Chọn A.
Ví dụ 3:Tìm số phức liên hợp của số phức 
Hướng dẫn:

Chọn B.
Ví dụ 4:Tìm số phức z thỏa mãn z – (2 + 3i)![]() = 1 – 9i .
= 1 – 9i .
A. z = -3 – i. B. z = -2 – i. C. z = 2 – i . D. z = 2 + i.
Hướng dẫn:
Gọi z = a + bi
z – (2 + 3i)![]() = 1 – 9i <=> a + bi – 2a + 2bi – 3ai – 3b = i – 9i
= 1 – 9i <=> a + bi – 2a + 2bi – 3ai – 3b = i – 9i
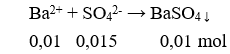
Vậy z = 2 – i
Chọn C.
Ví dụ 5:Cho số phức z = 3 + 4i. Tìm phần thực a và phần ảo b của số phức ![]() .
.
A. a = 3; b = 4 B. a = 3; b = -4 C. a = 4; b = 3 D. a = 4; b = -3
Hướng dẫn:
z = a + bi => ![]() = a – bi
= a – bi
vậy ![]() = 3 – 4i
= 3 – 4i
= >Phần thực a = 3 và phần ảo bằng b = -4
Chọn B.
Ví dụ 6:Cho số phức ![]() = 4 – 3i . Tìm phần thực và phần ảo của số phức z.
= 4 – 3i . Tìm phần thực và phần ảo của số phức z.
A. a = 3 ; b = 4 B. a = 3; b = -4 C. a = 4; b = 3 D. a = 4; b = -3
Hướng dẫn:
z = a + bi => ![]() = a – bi
= a – bi
vậy z = 4 + 3i
=> Phần thực a = 4 và phần ảo b = 3
Chọn C.
Ví dụ 7:Tìm số phức liên hợp của số phức 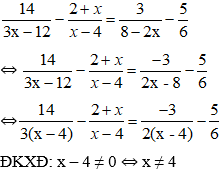
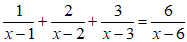
Hướng dẫn:
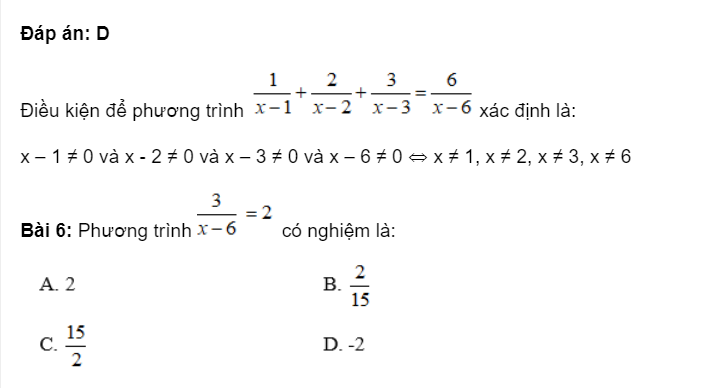
Chọn C.
Ví dụ 8:Tìm phần ảo b của số phức z thỏa mãn z + 2![]() = (2 – i)2(1 – i)
= (2 – i)2(1 – i)
A. b = 13 B.b = -13 C. b = -9 D. b = 9
Hướng dẫn:
Đặt z = x + yi
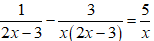
Chọn A.
Ví dụ 9:Tìm số phức iz + 2![]() = -1 – 8i thỏa mãn .
= -1 – 8i thỏa mãn .
A. z = 7 + 7i B. z = 5 – 2i. C. z = 2 + 5i. D. z = 1 – 2i.
Hướng dẫn:
Gọi z = a + bi khi đó ![]() = a – bi
= a – bi
Ta có: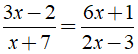
Vậy z = 2 + 5i
2. Số phức là gì?
Số phức là số được viết dưới dạng a + bi trong đó a, b là số thực và
, trong đó a và b là các số thức i là đơn vị ảo,
hay
. Trong biểu thức này, số a gọi là phần thực, b gọi là phần ảo của số phức.
Ngoài ra, số phức còn có thể biểu diễn trên mặt phẳng phức với trục hoành là trục số thực và trục tung chính là trục số ảo. Do đó một số phức a+ bi được xác định bằng một điểm có tọa độ (a,b). Theo đó một số phức nếu có phần thực bằng 0 thì gọi là số thuần ảo (hay số ảo), nếu có phần ảo bằng không thì trở thành số thực R.
3. Ứng dụng của số phức:
3.1. Số phức trong hình học và lượng giác:
Theo như khái niệm về số phức thì i chính là sự quay và chuyển hướng 90 độ nên số phức có một vai trò quan trọng trong việc giải các bài tập hình học phẳng và bài tập lượng giác. Các em chỉ cần áp dụng kiến thức số phức thì hoàn toàn có thể giải được các bài toán hình phẳng cũng như xử lý gọn các công thức lượng giác phức tạp.
Ngoài ra, số phức còn được ứng dụng vào giải các dạng bài tập liên quan khác như: phân tích đa thức ra thừa số, tính toán trong các bài tập về tích phân
3.2. Số phức trong các môn học khác và trong đời sống:
Khi các em học về số phức thì có thể dễ dàng nhận thấy số phức không chỉ được ứng dụng nhiều trong toán học mà còn cả trong vật lý. Các em có thể dễ dàng nhận thấy vật lý có liên quan rất nhiều đến đến hình học và nhiều đại lượng đo hướng mà nói về hướng là phải nói đến số phức. Vì như các em đã biết trong số phức thì phần số ảo i chính là đại diện cho sự quay 90 độ.
Ngoài ra, trong vật lý phần nguyên tử và khái niệm hàm sóng người ta cũng dùng số phức để để mô tả vật chất biến đổi theo thời gian. Việc sử dụng số phức trong vật lý sẽ giúp em biểu diễn thuận lợi hơn so với dùng số thực rất nhiều. Vì vậy, hãy ứng dụng tối đa phần kiến thức này trong quá trình học tập cũng như trong cuộc sống nhé!
4. Tổng hợp các khái niệm liên quan đến số phức:
Để có thể áp dụng làm các bài tập về số phức thì em cần nắm được các khái niệm liên quan đến số phức như sau:
4.1. Số phức liên hợp:
Định nghĩa: Số phức liên hợp có dạng: Z= a+ bi, số phức Z¯=a+bi được gọi là số phức liên hợp của Z.
4.2. Số phức nghịch đảo:
Có thể nói, số phức nghịch đảo, hay nghịch đảo của số phức Z (kí hiệu là
Ta có thể chứng minh:
Số phức dạng nghịch đảo của Z = a+bi là số phức
Số nghịch đảo của Z = a+bi # 0 là số
4.3. Số phức thuần ảo:
Định nghĩa: Số phức thuần ảo là khi phần thực a = 0 thì Z = bi thuộc R. Khi đó Z được gọi là số thuần ảo
4.4. Modun số phức:
Modun của số phức Z = a+bi là độ dài của vectơ u(a,b) biểu diễn số phức đó
Theo một định nghĩa khác thì số phức modun Z = a+bi (a,b∈R) là căn bậc hai số học của a2+b2
Ví dụ: 3+ 4i = 25 ⇒ 3+ 4i= 5
Ta dễ dàng nhận thấy trị tuyệt đối của số thực cũng chính là modun của số thực đó. Do đó đôi khi ta cũng có thể gọi modun của số phức là trị tuyệt đối của số phức. Modun số phức có công thức như sau:
Ký hiệu: |z| = a2+b2 + |z1z2| = |z1|.|z2| + ||z1||z2||≤|z1|+|z2| + z1/z2 = z1z2¯/|z2|2
Về mặt hình học, mỗi số phức Z = a+bi (a,b∈R ) được biểu diễn bởi một điểm M(z)= (a,b) trên mặt phẳng O_{xy} và ngược lại. Khi đó modun của Z được biểu diễn bởi độ dài đoạn thẳng OM(z). Rõ ràng, modun của z là một số thực không âm và nó chỉ bằng 0 khi Z=0.
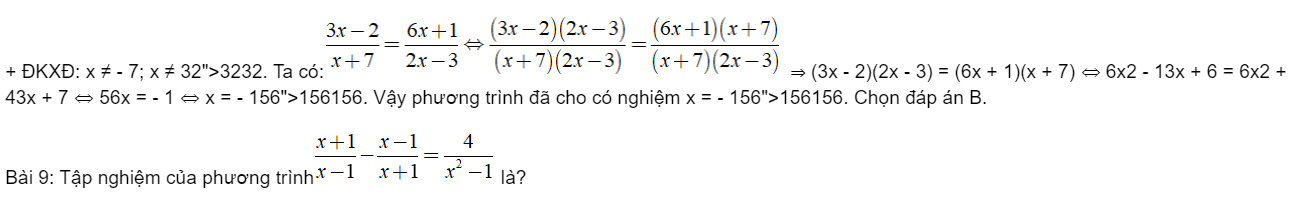
4.5. Argument của số phức:
Để hiểu về Argument của số phức giả sử ta có M(z) là điểm biểu diễn số phức z. Arg (z) là góc định hướng giữa chiều dương của trục thực và tia OM(z) thỏa mãn −n
Vậy nên rõ ràng nếu z=a+bi(a,b∈R) thì Arg(z)=Arctan(b/a)
5. Bài tập vận dụng:
Bài 1: Cho số phức z = 1 + 3i Tìm số phức ![]()
A. ![]() = 1 – 3i. B.
= 1 – 3i. B. ![]() = 3 – i. C.
= 3 – i. C. ![]() = 3 + i. D.
= 3 + i. D.![]() = 1 + 3i.
= 1 + 3i.
Lời giải:
Với z = 1 + 3i thì ![]() = 1 – 3i.
= 1 – 3i.
Chọn A.
Bài 2: Cho số phức z = -2 – 5i Tìm phần thực a và phần ảo b của số phức ![]() .
.
A. a = -2 ; b = 5 B. a = -2; b = -5 C. a = -5; b = 2 D. a = -5; b = -2
Lời giải:
z = a + bi => ![]() = a – bi
= a – bi
Nên ![]() = -2 + 5i vậy. Phần thực bằng a = -2 và phần ảo b = 5
= -2 + 5i vậy. Phần thực bằng a = -2 và phần ảo b = 5
Chọn A.
Bài 3:Tìm số phức liên hợp của số phức 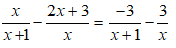
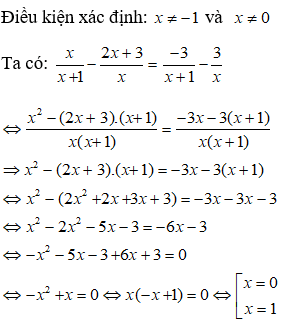
Lời giải:
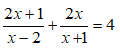
Chọn B.
Bài 4:Tìm số phức z thỏa mãn z – (2 + 3i)![]() = 1 – 9i .
= 1 – 9i .
A. z = -3 – i. B. z = -2 – i. C. z = 2 – i . D. z = 2 + i.
Lời giải:
Gọi z = a + bi
z – (2 + 3i)![]() = 1 – 9i <=> a + bi – 2a + 2bi – 3ai – 3b = i – 9i
= 1 – 9i <=> a + bi – 2a + 2bi – 3ai – 3b = i – 9i
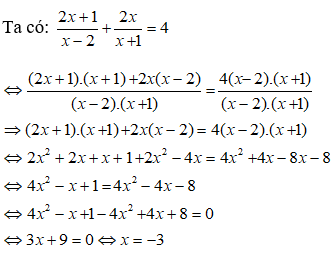
Vậy z = 2 – i
Chọn C.
Bài 5:Cho số phức z = 3 + 4i. Tìm phần thực a và phần ảo b của số phức ![]() .
.
A. a = 3; b = 4 B. a = 3; b = -4 C. a = 4; b = 3 D. a = 4; b = -3
Lời giải:
z = a + bi => ![]() = a – bi
= a – bi
vậy ![]() = 3 – 4i
= 3 – 4i
= >Phần thực a = 3 và phần ảo bằng b = -4
Chọn B.
Bài 6:Cho số phức ![]() = 4 – 3i . Tìm phần thực và phần ảo của số phức z.
= 4 – 3i . Tìm phần thực và phần ảo của số phức z.
A. a = 3 ; b = 4 B. a = 3; b = -4 C. a = 4; b = 3 D. a = 4; b = -3
Lời giải:
z = a + bi => ![]() = a – bi
= a – bi
vậy z = 4 + 3i
=> Phần thực a = 4 và phần ảo b = 3
Chọn C.




