Sơ đồ Hoocne là một thuật toán được biểu diễn dưới dạng sơ đồ cho phép chúng ta tìm nhanh thương và số dư trong phép chia một đa thức. Bài viết dưới đây cung cấp cho các bạn học sinh các cách sử dụng sơ đồ Hoocne để chia đa thức và một số bài tập vận dụng.
Mục lục bài viết
1. Giới thiệu về sơ đồ Hoocne:
Phân tích đa thức thành nhân tử là một bước quan trọng trong học toán, đặc biệt là khi nó liên quan đến nhân chia đơn thức và các biểu thức phức tạp hơn có chứa biến. Trong chương trình toán lớp 8 và các lớp sau, kiến thức này trở nên quan trọng khi giải các bài toán và ứng dụng trong thực tế.
Có nhiều phương pháp để phân tích đa thức thành nhân tử. Một trong những cách phổ biến là sử dụng các quy tắc đơn giản như rút gọn đa thức và chia nhỏ thành nhân tử. Ví dụ, xét đa thức ax^2 + bx + c, chúng ta có thể phân tích thành (px + q)(rx + s), với (p, q, r, s) là các hệ số phù hợp.
Tuy nhiên, không phải tất cả các bài toán đều dễ dàng như vậy. Có những đa thức phức tạp, và việc phân tích chúng đòi hỏi sự linh hoạt và sáng tạo. Một số phương pháp đặc biệt, như sử dụng định lý nhân tử đa thức, có thể được áp dụng để giải quyết những bài toán khó khăn này.
Hãy xem xét một ví dụ cụ thể. Xét đa thức (x^2 – 5x + 6). Để phân tích thành nhân tử, ta cần tìm hai số m và nsao cho m x n = 6 và m + n = -5. Trong trường hợp này, m = -2 và n = -3. Do đó,(x^2 – 5x + 6 = (x – 2)(x – 3).
Như vậy, khả năng phân tích đa thức thành nhân tử không chỉ giúp hiểu rõ về cấu trúc của đa thức mà còn là một công cụ hữu ích trong việc giải các bài toán toán học và ứng dụng thực tế.
Sơ đồ Hoocne là một phương pháp hữu ích trong việc giải bài toán phép chia đa thức, đặc biệt là khi chia cho đa thức bậc nhất , trong đó là một số thực bất kỳ. Phương pháp này giúp chúng ta dễ dàng xác định được thương và dư của phép chia một đa thức cho .
Cách thức thực hiện sơ đồ Hoocne là bắt đầu với việc viết các hệ số của đa thức lên một dãy số và đặt bên dưới nó. Sau đó, ta thực hiện các bước nhất định để xác định hệ số của thương và dư.
2. Cách sử dụng sơ đồ Hoocne (Horner) để chia đa thức:
2.1 Sử dụng kiến thức Toán học:
Sơ đồ Horner (Hoocne/ Hoắc – le/ Hắc – le) dùng để tìm đa thức thương và dư trong phép chia đa thức f(x) cho đa thức x – α , khi đó ta thực hiện như sau:
Giả sử cho đa thức
Khi đó đa thức thương và đa thức dư được xác định theo lược đồ sau:

Ta được cách làm theo các bước như sau:
Bước 1: Sắp xếp các hệ số của đa thức theo ẩn giảm dần và đặt số
vào cột đầu tiên của hàng thứ 2. Nếu trong đa thức mà khuyết ẩn nào đó thì ta coi hệ số của nó bằng 0 và vẫn phải điền vào lược đồ.
Bước 2: Cột thứ 2 của hàng 2 ta hạ hệ số ở hàng trên xuống. Đây chính là hệ số đầu tiên của
tìm được, tức là
.
Bước 3: Lấy số nhân với hệ số vừa tìm được ở hàng 2 rồi cộng chéo với hệ số hàng 1 (Ví dụ nếu ta muốn tìm hệ số
ở hàng thứ hai, trước tiên ta sẽ lấy
nhân với hệ số
sau đó cộng với hệ số
ở hàng trên; tương tự như vậy nếu ta muốn tìm hệ số
ở hàng thứ hai, trước tiên ta sẽ lấy
nhân với hệ số
sau đó cộng với hệ số
ở hàng trên,….)
Quy tắc nhớ: NHÂN NGANG, CỘNG CHÉO.
Bước 4: Cứ tiếp tục như vậy cho tới hệ số cuối cùng và kết quả ta sẽ có
hay
* Chú ý:
+ Bậc của đa thức g(x) luôn nhỏ hơn bậc của đa thức f(x) 1 đơn vị vì đa thức chia có bậc là 1.
+ Nếu r=0 thì đa thức f(x) chia hết cho đa thức g(x) và sẽ là một nghiệm của đa thức f(x). Trong trường hợp này chính là phân tích đa thức thành nhân tử. Để tìm được
, ta sẽ nhẩm một nghiệm nguyên của đa thức f(x), a chính là nghiệm mà ta vừa nhẩm được.
Khi thực hành giải toán, bất cứ khi nào bạn cần chia đa thức cho đa thức mà đa thức chia có dạng x−c thì nên sử dụng sơ đồ Hoocne để thực hiện cho nhanh.
Ngoài việc giải nhanh ra thì sử dụng phương pháp này sẽ giúp bạn tránh khỏi những sai sót không đáng có. Không những thế, khi kết hợp sơ đồ Hoocne với định lý Bơdu thì chúng ta còn có thể tính nhanh giá trị của f(c)=r, rất hữu ích khi f(x) có bậc cao.
3. Một số bài tập trắc nghiệm vận dụng:
Bài 1: Kết quả của phép chia ( 7×3 – 7x + 42 ):( x2 – 2x + 3 ) là ? A. – 7x + 14 B. 7x + 14 C. 7x – 14 D. – 7x – 14
Lời giải:
Ta có phép chia
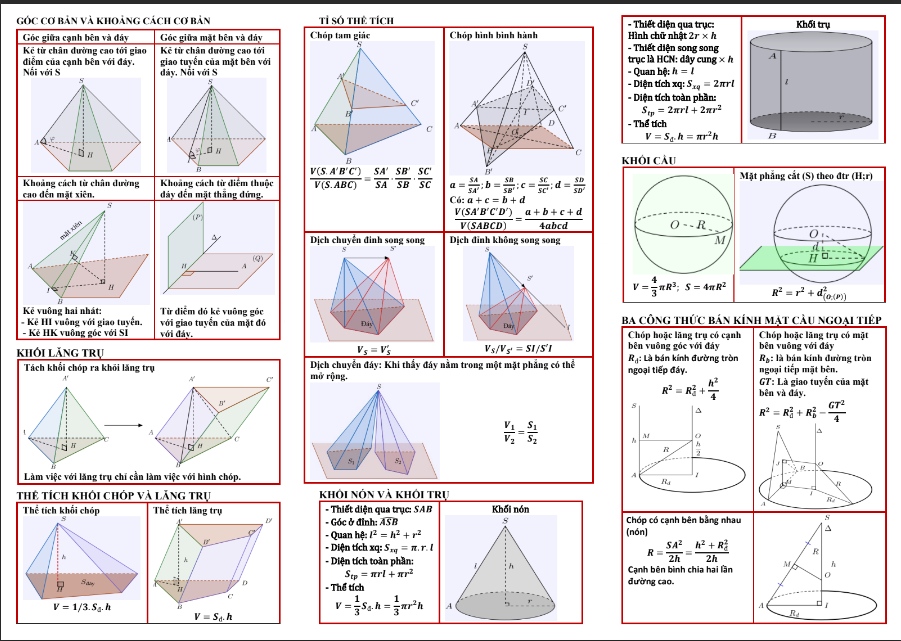
Chọn đáp án B.
Bài 2: Phép chia x3 + x2 – 4x + 7 cho x2 – 2x + 5 được đa thức dư là ?
A. 3x – 7. B. – 3x – 8.
C. – 15x + 7. D. – 3x – 7.
Lời giải
Ta có pchiai

Dựa vào kết quả của phép chia trên,, ta có đa thức dư là – 3x – 8.
Chọn đáp án B.
Bài 3: Hệ số a thỏa mãn để 4×2 – 6x + a chia hết có x – 3 là ?
A. a = – 18. B. a = 8.
C. a = 18. D. a = – 8.
Lời giải:
Ta có phép chia

Phép chia trên có số dư là ( a + 18 )
Để 4×2 – 6x + a chia hết có x – 3 ⇔ a + 18 = 0 ⇔ a = – 18.
Chọn đáp án A.
Bài 4: Thực hiện phép chia: (4×4 + x + 2×3 – 3×2) : (x2 + 1) ta được số dư là :
A. – x + 7
B. 4×2 + 2x – 7
C. 4×2 – 2x + 7
D. x – 7
Lời giải:
Ta có: 4×4 + x + 2×3 – 3×2 = 4×4 + 2×3 – 3×2 + x
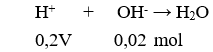
Vậy: (4×4 + x + 2×3 – 3×2) = (4×2 + 2x – 7 ).(x2 +1) – x + 7
Chọn đáp án A
Bài 5: Thực hiện phép chia (3×3 + 2x + 1 ) : (x + 2) ta được đa thức dư là :
A. 10 B. -9
C. – 15 D. – 27
Lời giải:
Ta có:
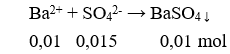
Vậy số dư của phép chia đã cho là –27
Chọn đáp án D
Bài 6: Thực hiện phép chia (-4×4 + 5×2 + x ) : (x2 + x) ta được kết quả là:
A. – 4×4 + 5×2 + x = (x2 + x).(-4×2 – 4x + 9) – 6x
B. – 4×4 + 5×2 + x = (x2 + x).(4×2 + 4x + 9) + 12x
C. – 4×4 + 5×2 + x = (x2 + x).(-4×2 + 4x + 9) – 8x
D. – 4×4 + 5×2 + x = (x2 + x). ( 4×2 – 4x + 9) + 10x
Lời giải:
Ta có:
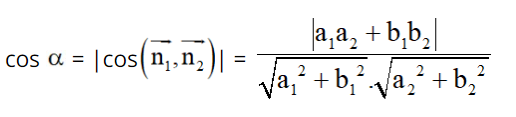
Vậy –4×4 + 5×2 + x = (x2 + x).(-4×2 + 4x + 9) – 8x
Chọn đáp án C
Bài 7: Cho phép chia: (x3 + 9×2 + 27x + 27) : (x + 3). Tìm khẳng định sai?
A. Đây là phép chia hết
B. Thương của phép chia là: (x + 3)2
C. Thương của phép chia là: x2 + 6x + 9
D. Số dư của phép chia là: x – 3 .
Lời giải:
Áp dụng hằng đẳng thức đáng nhớ:
(a + b)3 = a3 + 3a2b + 3ab2 + b3 ta được:
(x3 + 9×2 + 27x + 27) : (x + 3) = (x + 3)3 : (x + 3) = (x + 3)2 = x2 + 6x +9
Vậy phéo chia đã cho là phép chia hết có thương là: (x + 3)2 = x2 + 6x + 9.
Chọn đáp án D
Bài 8: Thực hiện phép chia: (x2y + 4xy + 3y ) : (x + 1) ta được thuơng là:
A. xy + 3 B. x + 3y
C. x + y + 3 D. y. (x + 3)
Lời giải:
Ta có: x2y + 4xy + 3y = y.(x2 + 4x + 3)
= y.[(x2 + x ) + (3x + 3)]
= y.[x.(x + 1) + 3(x + 1)]
= y.(x + 3).(x+1 )
Vậy: (x2y + 4xy + 3y ) : (x + 1) = y.(x + 3).(x + 1) : (x + 1) = y.(x + 3).
Chọn đáp án D
Bài 9: Tìm a để phép chia (x3 – 4x + a): (x – 2) là phép chia hết:
A. a = 0 B. a = 4
C. a = -8 D. a = 8
Lời giải:
Ta có:
Để phép chia đã cho là phép chia hết khi và chỉ khi phần dư bằng 0. Do đó, a =0
Chọn đáp án A
Bài 10: Làm tính chia: (9x3y2 + 10x4y5 – 8x2y2) : x2y2
A. 9x + 10x2y2 B. 9 + 10x2y2 – 8
C. 9x + 10x2y3 – 8 D. Đáp án khác
Lời giải:
Ta có: (9x3y2 + 10x4y5 – 8x2y2) : x2y2
= 9x3y2 : x2y2 + 10x4y5 : x2y2 – 8x2y2 : x2y2
= 9x + 10x2y3 – 8
Chọn đáp án C




