Mời bạn đọc cùng tìm hiểu về cách giải phương trình bậc 3 và ví dụ bài tập vận dụng
Mục lục bài viết
1. Phương trình bậc 3 là gì?
Trong đại số, một phương trình bậc ba có một biến là một biểu thức có dạng

trong đó a khác 0.
Lời giải của đẳng thức này được gọi là các không điểm của hàm số bậc ba được định nghĩa bởi vế trái của biểu thức. Nếu tất cả những hệ số a, b, c và d của phương trình là số thực, thì nó có ít nhất 1 không điểm (điều này đúng với mọi phương trình bậc lẻ). Tất cả các không điểm của phương trình bậc ba có thể được tìm ra bằng những cách sau:
Phương pháp đại số, nghĩa là chúng có thể được biểu thị bằng một công thức bậc ba liên quan đến bốn hệ số, bốn phép tính số học cơ bản và căn bậc hai, căn bậc ba.
Phương pháp lượng giác, các phép gần đúng bằng số của các giá trị căn có thể được tìm thấy bằng cách sử dụng các thuật toán tìm nghiệm như phương pháp của Newton.
Các hệ số không cần thiết phải là số thực. Các nghiệm của phương trình bậc ba không nhất thiết phải thuộc cùng trường với hệ số. Ví dụ, một số phương trình bậc ba với hệ số hữu tỉ có nghiệm là số vô tỉ (hay thậm chí là số phức).
2. Cách giải phương trình bậc 3:
2.1. Cách giải phương trình bậc 3 dạng x3 = a:
Cách giải dạng phương trình này sử dụng căn thức bậc 3, ta có:
![]()
2.2. Cách giải phương trình bậc 3 dạng ax3 + bx2 + cx + d = 0
Với dạng phương trình này đề thường cho trước 1 nghiệm (hoặc ta dễ dàng tính nhẩm được nghiệm của pt, thường là 0; ±1/2: ±1; ±2).
– Nếu x = α là nghiệm của phương trình ax3 + bx2 + cx + d = 0 thì
ax3 + bx2 + cx + d = (x – α).f(x)
– Để tìm f(x) ta lấy đa thức ax3 + bx2 + cx + d chia cho (x – α).
– Giả sử f(x) = ax2 + Bx + C, khi đó phương trình ax3 + bx2 + cx + d = 0 được đưa về phương trình dạng tích (x – α).(ax2 + Bx + C) = 0.
* Lưu ý: Để tìm f(x) ngoài cách chia đa thức ta có thể sử dụng sơ đồ Hoocne bậc 3 sau:

Khi đó: ax3 + bx2 + cx + d = (x – α).(ax2 + Bx + C)
ax3 + bx2 + cx + d = 0
⇔ (x – α).(ax2 + Bx + C) = 0
2.3. Một số lưu ý khi giải phương trình bậc 3:
Nếu ![]() thì phương trình có nghiệm là 1
thì phương trình có nghiệm là 1
Nếu![]() thì phương trình có nghiệm là −1
thì phương trình có nghiệm là −1
Nếu phương trình có nghiệm nguyên thì chỉ có thể là một trong các ước của d
Nếu phương trình có nghiệm hữu tỉ ![]() thì p,q lần lượt theo thứ tự là ước của d và a
thì p,q lần lượt theo thứ tự là ước của d và a
Nếu![]() thì phương trình có nghiệm là
thì phương trình có nghiệm là ![]()
Phương trình bậc ba có không quá ba nghiệm
Với phương trình bậc ba chỉ cần tìm được một nghiệm xem như chúng ta đã hoàn thành 75% lời giải rồi.
Lúc này, bạn chỉ cần chia vế trái của phương trình cho x−x0 (x0 là một nghiệm của phương trình) thì lập tức được một tam thức bậc hai.
Mà Tam thức bậc hai / phương trình bậc hai thì chúng ta có thể giải được một cách dễ dàng.
Có nhiều phương trình bậc ba có hệ số nguyên nhưng vẫn không có nghiệm nguyên, nghiệm hữu tỉ.
Có nhiều phương trình bậc ba có hệ số nguyên nhưng vẫn có nghiệm thực.
3. Một số bài tập và hướng dẫn chi tiết giải phương trình bậc 3:
* Bài tập 1: Giải phương trình bậc 3 sau: x3 = 8
* Lời giải:
– Ta có:![]()
![]()
Vậy x = 2 là nghiệm của phương trình.
* Bài tập 2: Giải phương trình bậc 3 sau: 2x3 = -128
* Lời giải:
– Ta có: ![]()
![]()
Vậy x = -4 là nghiệm của phương trình.
* Bài tập 3: Giải phương trình bậc 3 sau: 2x3 + 5x2 – x – 6 = 0.
* Lời giải:
– Dễ dàng nhận thấy các hệ số của phương trình bậc 3 là:
a + b + c + d = 2 + 5 – 1 – 6 = 0 nên có thể nhẩm được phương trình bậc 3 này có 1 nghiệm x = 1.
Vì x = 1 là một nghiệm của phương trình nên lấy đa thức (2x3 + 5x2 – x – 6) chia cho
(x – 1). Ta sử dụng sơ đồ Hooc-ne để chia:
| x | 2 | 5 | -1 | -6 |
| 1 | 2 | 1.2+5=7 | 1.7+(-1)=6 | 1.6+(-6)=0 |
Vậy 2x3 + 5x2 – x – 6 = (x – 1)(2x2 + 7x + 6)
Khi đó: 2x3 + 5x2 – x – 6 = 0
⇔ (x – 1)(2x2 + 7x + 6) = 0
⇔ (x – 1)= 0 hoặc (2x2 + 7x + 6) = 0
Xét phương trình: x – 1 = 0 ⇔ x = 1
Xét phương trình: 2x2 + 7x + 6 = 0 có ∆ = 72 – 4.2.6 = 1 > 0 nên phương trình có 2 nghiệm:
x1 = (-7 + 1)/4 = -3/2;
x2 = (-7 – 1)/4 = -2
Vâ
Tập nghiệm của phương trình S={-2;-3/2;1}.
* Bài tập 4: Tìm nghiệm của phương trình bậc 3 sau: 3x3 – 2x2 – 5x + 4 = 0 biết x = 1 là một nghiệm của phương trình.
* Lời giải:
Vì x = 1 là một nghiệm của phương trình nên lấy đa thức (3x3 – 2x2 – 5x + 4) chia cho (x – 1). Ta sử dụng sơ đồ Hooc-ne để chia:
| x | 3 | -2 | -5 | 4 |
| 1 | 3 | 1.3+(-2)=1 | 1.1+(-5)=-4 | 1.(-4)+4=0 |
Vậy 3x3 – 2x2 – 5x + 4 = (x – 1).(3x2 – 2x – 5)
Khi đó: x3 – 2x2 – 5x + 4 = 0
⇔ (x – 1).(3x2 – 2x – 5) = 0
⇔ x – 1 = 0 hoặc 3x2 – 2x – 5 = 0
Xét phương trình: x – 1 = 0 ⇔ x = 1
Xét phương trình: 3x2 – 2x – 5 = 0 có ∆ = (-2)2 – 4.3.(-5)= 64 nên phương trình có 2 nghiệm: x1 = -1 và x2 = 5/3.
(có thể thấy ngay phương trình: 3x2 – 2x – 5 = 0 có các hệ số a – b + c = 0 nên có 1 nghiệm x = -1 và nghiệm còn lại x = -c/a = 5/3)
Vây phương trình có 3 nghiệm: x = 1; x = -1; x = 5/3.
* Bài tập 5: Tìm m để phương trình bậc 3 sau có đúng 2 nghiệm phân biệt:
(x – 2)(x2 + mx + m2 – 3) = 0 (*)
* Lời giải:
– Phương trình (*)⇔ ![]()
Phương trình (1) có 1 nghiệm x = 2 nên để phương trình (*) có đúng 2 nghiệm thì phương trình (2) phải có nghiệm kép khác 2 hoặc có 2 nghiệm phân biệt trong đó một nghiệm bằng 2.
+) TH1: phương trình (2) có nghiệm kép khác 2
⇔ Phương trình (2) có: ∆ = 0 và x = 2 không là nghiệm của (2)

+) TH2: Phương trình (2) có 2 nghiệm phân biệt trong đó một nghiệm bằng 2
Thay x = 2 vào phương trình (2) ta được:
m2 + 2m + 1 = 0
⇔ (m + 1)2 = 0
⇔ m = -1
Với m = -1 thì phương trình (2) trở thành: x2 – x – 2 = 0
Phương trình này có a – b + c = 0 nên có 2 nghiệm: x1 = -1, x2 = -c/a = 2
Suy ra m = -1 (thỏa mãn)
Vậy m = -1, m = 2, m = -2 thì phương trình (*) có đúng 2 nghiệm phân biệt.
*Bài tập 6: Tìm các nghiệm của phương trình x3 + x2 = 12 (1), biết x = 2 là một nghiệm của phương trình
Giải
Phương trình (1) ⇔ x3+x2-12 = 0
Vì x = 2 là một nghiệm của phương trình nên lấy đa thức (x3 + x2 – 12) chia cho
(x – 2). Ta sử dụng sơ đồ Hooc-ne để chia:

Vậy x3 + x2 – 12 = (x – 2).( x2 + 3x + 6)

Xét phương trình: x – 2 = 0 ⇔ x = 2
Xét phương trình: x2 + 3x + 6 = 0 có ∆ = 32 – 4.1.6 = -15 < 0 nên phương trình vô nghiệm
Vây phương trình có nghiệm duy nhất x = 2
* Bài tập 7: Tìm m để phương trình: (x – 2)(x2 + mx+ m2 – 3) = 0 (1) có đúng 2 nghiệm phân biệt
Giải
Phương trình (1) 
Phương trình (*) có 1 nghiệm x = 2 nên để phương trình (1) có đúng 2 nghiệm thì phương trình (**) phải có nghiệm kép khác 2 hoặc có 2 nghiệm phân biệt trong đó một nghiệm bằng 2
+ TH1: phương trình (**) có nghiệm kép khác 2 ⇔ phương trình (**) có
∆ = 0 và x = 2 không là nghiệm của (**)

+ TH2: phương trình (**) có 2 nghiệm phân biệt trong đó một nghiệm bằng 2
Thay x = 2 vào phương trình (**) ta được:

Với m = -1 thì phương trình (**) trở thành: x2-x-2 = 0
Phương trình này có a – b + c = 0 nên có 2 nghiệm x = -1, x = 2
Suy ra m = -1 thỏa mãn
Vậy m = -1, m = 2, m = -2 là các giá trị cần tìm.
*Bài tập 8: Tính tổng các nghiệm của phương trình, biết x = -3 là một nghiệm của phương trình
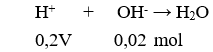
Giải
Vì x = -3 là một nghiệm của phương trình nên ta lấy đa thức (2x3 + x2 – 13x + 6)chia cho (x + 3). Ta sử dụng sơ đồ Hooc-ne để chia
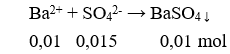
Xét phương trình x + 3 = 0 ⇔ x = -3
Xét phương trình 2x2 – 5x + 2 = 0 có ∆ = (-5)2 – 4.2.2 = 9 > 0 nên phương trình có hai nghiệm phân biệt: x = 2, x = 1/2
Vậy tổng các nghiệm của phương trình là: ![]()
Đáp án là D
* Bài tập 9: Tìm m để phương trình (x + 1)(x2 + 2mx + 4) = 0 (1) có 3 nghiệm phân biệt và tổng các nghiệm bằng 3
A. m = 1
B. m = 6
C. Không tồn tại m
D. m = 0
Giải
Phương trình (1) 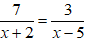
Phương trình (*) có 1 nghiệm x1 = -1 nên để phương trình (1) có 3 nghiệm thì phương trình (**) phải có 2 nghiệm phân biệt x2, x3 khác x1 = -1
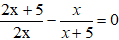
Vì x2, x3 là hai nghiệm của phương trình (**) nên x2 + x3 = -2m
Tổng các nghiệm của phương trình (1) là: x1 + x2 + x3 = -1 – 2m = 3 ⇔ m = -2
m = -2 không thỏa mãn điều kiện 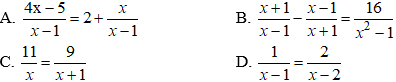 nên loại
nên loại
Vậy không có giá trị nào của m thỏa mãn đề bài




