Hệ thức lượng trong tam giác vuông là dạng kiến thức quan trọng trong chương trình toán phổ thông, thường xuyên xuất hiện trong các bài kiểm tra, bài thi. Bài viết Cách chứng minh các hệ thức lượng trong tam giác vuông với phương pháp giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập. Mời các bạn cùng theo dõi!
Mục lục bài viết
1. Cách chứng minh hệ thức lượng trong tam giác vuông:
1. Chọn các tam giác vuông thích hợp chứa các đoạn thẳng có trong hệ thức. Tính các đoạn thẳng đó nhờ các hệ thức về cạnh và đường cao.
2. Liên kết các giá trị trên và rút ra hệ thức phải chứng minh.
Cho ΔABC, góc A = 900, AH ⊥ BC, BC = a, AB = c, AC = b, AH = h thì:
+) BH = c’ được gọi là hình chiếu của AB trên cạnh huyền BC
+) CH = b’ được gọi là hình chiếu của AC trên cạnh huyền BC
Khi đó ta có các hệ thức về cạnh và đường cao trong tam giác vuông:
1) b2 = ab’; c2 = ac’
2) h2 = b’c’
3) ha = bc
4) 1/ h2 = 1/ b2 + 1/ c2
5) a2 = b2 + c2( Định lý Pytago)
2. Ví dụ minh họa:
Ví dụ 1: Cho Δ ABC vuông tại A, đường cao AH. Chứng minh rằng:
BH2 + CH2 = AB2 + AC2 – 2AH2
Bài giải:
+) Áp dụng hệ thức lượng cho ΔABC vuông tại A, đường cao AH ta có:
AH2 = BH.CH (1)
+) Áp dụng định lý Py – ta – go cho tam giác ABC có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = (BH + CH)2
⇔ AB2 + AC2 = BH2 + CH2 + 2.BH.CH (2)
Thay (1) vào (2) ta được:
⇔ AB2 + AC2 = BH2 + CH2 + 2AH2
⇔ BH2 + CH2 = AB2 + AC2 – 2AH2
Vậy BH2 + CH2 = AB2 + AC2 – 2AH2
Ví dụ 2: Cho ΔABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB và AC. Hãy chứng minh
3AH2 + BD2 + CE2 = BC2
Bài giải:
+) Xét ΔBHD vuông tại D, áp dụng định lý Py – ta – go ta có: BD2 = BH2 – DH2
+) Xét ΔCHE vuông tại E, áp dụng định lý Py – ta – go ta có: CE2 = CH2 – EH2
+) Xét ΔABC vuông tại A, áp dụng định lý Py – ta – go ta có: BC2 = AB2 + AC2
+) Xét ΔAHE vuông tại E, áp dụng định lý Py – ta – go ta có: AH2 = AE2 + EH2
Ta có:
3AH2 + BD2 + CE2 = BC2
⇔ 3AH2 + (BH2 – DH2) + (CH2 – EH2) = AB2 + AC2 ( Định lý Py – ta – go cho ba tam giác vuông ΔBHD, ΔCHE và ΔABC )
⇔ 3AH2 + BH2 + CH2 – (EH2 + DH2) = AB2 + AC2 (*)
+) Xét tứ giác ADHE có:
![]() = 900 (gt)
= 900 (gt)
⇒ Tứ giác ADHE là hình chữ nhật ⇒ DH = AE
Thay DH = AE vào (*) ta có:
(*) ⇔ 3AH2 + BH2 + CH2 – (EH2 + AE2) = AB2 + AC2
⇔ 3AH2 + BH2 + CH2 – AH2 = AB2 + AC2 (do AH2 = AE2 + EH2)
⇔ BH + CH + 2AH = AB + AC (luôn đúng theo ví dụ 1)
Vậy 3AH2 + BD2 + CE2 = BC2.
Ví dụ 3: Cho ΔABC vuông tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu vuông góc của H trên AB và AC. Chứng minh rằng:
a) AM.AB = AN. AC
b) HB.HC = MA.MB + NA.NC
Bài giải:
a) Xét ΔABH có: AH ⊥ BC
⇒ ΔABH vuông tại H
Mà HM AB ⇒ AM.AB = AH2 ( Hệ thức lượng trong tam giác vuông)
Chứng minh tương tự: AN.AC = AH2
Vậy suy ra AH2 = AM.AB = AN.AC (đpcm)
b)
+) Xét tam giác ABC vuông tại A có AH ⊥ BC (gt)⇒ AH2 = BH.CH( Hệ thức lượng trong tam giác vuông)
Chứng minh tương tự:
Xét tam giác vuông ABH ta có: MH2 = BM.AM
Xét tam giác vuông ACH có: NH2 = AN.CN
+) Xét tứ giác AMHN có:
![]() = 900 (gt)
= 900 (gt)
⇒ Tứ giác AMHN là hình chữ nhật ⇒ NH = AM
+) Xét tam giác vuông AMH có:
AH2 = AM2 + MH2 ( Định lý Py – ta – go)
⇔ AH2 = MH2 + NH2 ( do AM = NH – cmt)
⇔ BH.CH = BM.AM + AN.Cn (đpcm)
Vậy HB.HC = MA.MB + NA.NC.
Ví dụ 4: Cho ΔABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB và AC. Hãy chứng minh:
a) 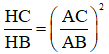
b) AH3 = BC.BD.CE
Bài giải:
a) Áp dụng hệ thức lượng cho ΔABC vuông tại A, đường cao AH ta có:
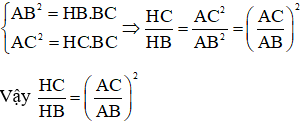
b)
+) Xét ΔABH có: AH ⊥ BC
⇒ ΔABH vuông tại H
Mà HD ⊥ AB ⇒ BH2 = BD.AB ( Hệ thức lượng trong tam giác vuông)
Chứng minh tương tự ta có: CH2 = EC.AC
+) Xét tam giác ABC có:
AH2 = BH.CH ( Hệ thức lượng trong tam giác vuông)
⇔ AH4 = BH2.CH2
⇒ AH4 = BD.AB.AC.EC
⇔ AH4 = BD.CE.(AB.AC)
Mặt khác AB.AC = AH.BC ( Hệ thức lượng trong tam giác vuông)
⇔ AH4 = BD.CE.AH.BC
Do AH > 0 nên chia cả hai vế cho AH ta được:
⇔ AH3 = BD.CE.BC (đpcm)
Vậy AH3 = BC.BD.CE.
Ví dụ 5: Cho tam giác ABC vuông tại A. Trên AB lấy điểm D, trên AC lấy điểm E. Chứng minh: CD2 + BE2 = CB2 + DE2
Bài giải:
Áp dụng định lý Py – ta – go cho các tam giác ΔABC, ΔABE có:
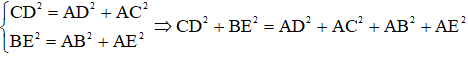 (1)
(1)
Mặt khác áp dụng định lý Py – ta – go cho ΔABC và ΔADE có:
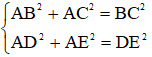 (2)
(2)
Từ (1) và (2) suy ra: CD2 + BE2 = CB2 + DE2 – đpcm
Ví dụ 6: Cho tam giác ABC cân tại A, ba đường cao AD, BE, CF. Đường thẳng qua B và song song với CF cắt đường thẳng AC tại H. Chứng minh rằng:
a) AC là trung bình nhân của AE và AH
b) ![]()
Bài giải:
a) Ta có BH vuông góc AB
Xét ΔABH vuông tại B có BE là đường cao nên AB2 = AH.AE
Mà ΔABC cân tại A ⇒ AB = AC do đó AC2 = AB2 = AH.AE
Vậy AC2 = AH.AE.
b)
+) Xét ΔABC cân tại A có AD là đường cao
⇒ AD cũng đồng thời là đường trung tuyến ⇒ BD = CD = 1/2 BC
Từ D dựng DK ⊥ AB (K ∈ AB)
Mà CF ⊥ AB (gt) ⇒ KD // CF
+) Xét ΔBFC có: BK = FK
DK là đường trung bình của ΔBFC ⇒ KD = 1/2 CF
+) Xét ΔABD vuông tại D có: KD ⊥ AB (gt)
![]() (Hệ thức lượng trong tam giác vuông)
(Hệ thức lượng trong tam giác vuông)
Mặt khác nên ta được:
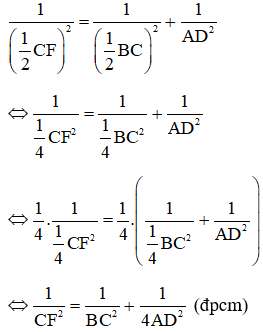
Ví dụ 7: Cho góc xOy và tia Oz nằm giữa hai tia Ox và Oy. Từ điểm A trên tia Oz vẽ AH ⊥ Ox, AK ⊥ Oy. Gọi E và F lần lượt là hình chiếu của H và K trên Oz, gọi B là giao điểm của HK và Oz. Chứng minh rằng:
![]()
Bài giải:
+) Xét ΔOHA vuông tại H có HE ⊥ OA (gt)
⇒ HE2 = EA.EO( Hệ thức lượng trong tam giác vuông) (1)
+) Xét ΔOKA vuông tại H có KF ⊥ OA (gt)
⇒ KF2 = FA.FO ( Hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) suy ra:
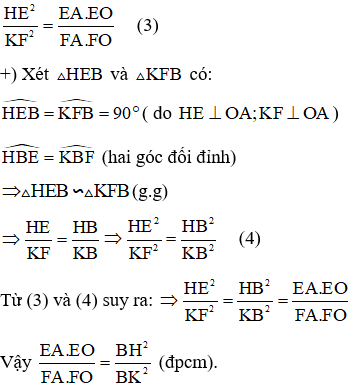
3. Bài tập luyện tập:
Bài 1. Cho tam giác CDE nhọn, đường cao CH. Gọi M, N theo thứ tự là hình chiếu của H lên CD, CE. Chứng minh:
a) CD.CM = CE.CN;
b) ∆CMN ∼ ∆CED.
Bài 2. Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B . Tia DI và tia CB cắt nhau ở K . Kẻ đường thẳng qua D , vuông góc với DI, cắt đường thẳng BC tại L. Chứng minh: Tam giác DIL là tam giác cân
Bài 3. Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên các cạnh AB, AC. Chứng minh: MN3 = BM.CN.BC
Bài 4. Cho tam giác ABC vuông tại C có đường cao CK.
a) Biết AB = 10cm, AC = 8cm. Hãy tính BC, CK, BK, AK;
b) Gọi H và I theo thứ tự là hình chiếu của K lên BC và AC. Chứng minh BC.CH = AC.IC.
Bài 5
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nắm trên đường nào?
Bài 6. Cho tam giác ABC có D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của DAE
b) Giả sử DAE = 60 độ. Tính các góc còn lai của tam giác DAE.
Bài 7. Cho tam giác ABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a) Chứng minh DABC = DABD
b) Trên tia đối của tia AB, lấy điểm M. Chứng minh DMBD = D MBC.
Bài 8: Cho tam giác ABC vuông tại A. Biết AC=57. Đường cao là AH = 15cm. Hãy áp dụng hệ thức lượng trong tam giác vuông, hãy tính HB, HC.
THAM KHẢO THÊM:




