Các quy tắc tính xác suất? Bài tập vận dụng tính xác suất?

1. Xác suất là gì?

Xác suất là khả năng xuất hiện một sự kiện, hiện tượng (gọi là biến cố). Xác suất được tính bằng một số nằm trong khoảng từ 0 (biến cố không thể xảy ra) đến 1 (biến cố chắc chắn xảy ra). Nhờ kết quả quan sát trong quá khứ hay cơ sở kinh nghiệm mà mọi người hầu như đều biết ước tính xác suất. Họ dựa và số lần xuất hiện hay tần suất tương đối của các hiện tượng và khái quát hoá kinh nghiệm này. Ở một số trường hợp, người ta dễ dàng ước tính tỷ trọng của các tình huống trong đó một sự kiện xuất hiện.

Ví dụ, về tính xác suất sự xuất hiện mặt ngửa hay úp của việc tung đồng xu, đồng xu đồng nhất và cần đối là 50%, vì kinh nghiệm cho thấy nếu tung đồng xu nhiều lần, thì số lần được mặt sấp và mặt ngừa là 50:50. Tuy nhiên, khi ước tính xác suất trong các tình huống kinh doanh, thường người ta có thể không có hoặc chỉ có rất ít kinh nghiệm hữu ích cho việc tính toán tấn suất tương đối của một biến cố.

2. Không gian mẫu và sự kiện:

Tập các kết quả có thể xảy ra của một thí nghiệm được gọi là không gian mẫu (ký hiệu: $\Omega$). Mỗi phần tử $\omega$ trong $\Omega$ được gọi là một kết quả (một điểm hay phần tử trong không gian mẫu). Mỗi tập con của $\Omega$ được gọi là một biến cố. 

Ví dụ:

Tung đồng xu kết quả có thể là sấp hoặc ngửa. Gọi AA là biến cố “sấp” và BB là biến cố “ngửa”. Tung đồng xu hai lần, không gian mẫu là $\Omega =\{AA,\; AB,\; BA,\; BB\}$.

Biến cố lần tung đầu tiên sấp trong thí nghiệm là $A=\{AA,\; AB\}$

3. Các loại xác suất:

3.1. Quy tắc cộng xác suất:

Nếu hai biến cố A và B xung khắc thì P(A ∪ B)=P(A)+P(B)

Mở rộng quy tắc cộng xác suất

Cho k biến cố A₁,A₂,A₃…..A_k đôi một xung khắc. Khi đó:

P(A₁ ∪ A₂ ∪ A₃….. ∪ A_k )=P(A₁ )+P(A₂)+…+P(A_k )

P(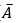)=1-P(A)

Giả sử A và B là hai biến cố tùy ý cùng liên quan đến một phép thử.

Lúc đó: P(A ∪ B)=P(A)+P(B)

Cho hai biến cố A và B cùng liên quan đến một phép thử T. Biến cố “A hoặc B xảy ra” được gọi là hợp của hai biến cố A và B, kí hiệu A∪B.

Nếu gọi ΩA là tập hợp mô tả các kết quả thuận lợi cho A, ΩB là tập hợp mô tả các kết quả thuận lợi cho B, thì tập hợp các kết quả thuận lợi cho A∪B là ΩA∪ΩB.

Tổng quát: Cho k biến cố A1,A2,…,Ak cùng liên quan đến một phép thử T. Biến cố “Có ít nhất một trong các biến cố A1,A2,…,Ak xảy ra” được gọi là hợp của k biến cố A1,A2,…,Ak, kí hiệu A1∪A2∪…∪Ak.

Biến cố xung khắc:

Cho hai biến cố A và B cùng liên quan đến một phép thử T. Nếu biến cố này xảy ra mà biến cố kia không xảy ra thì hai biến cố A và B gọi là xung khắc.

Biến cố đối:

Cho biến cố A khi đó biến cố “Không xảy ra A” được gọi là biến cố đối của A, kí hiệu A―.

Hai biến cố đối nhau là hai biến cố xung khắc. Tuy nhiên hai biến cố xung khắc chưa chắc là hai biến cố đối nhau

Cho biến cố A. Xác suất của biến cố đối A― là P(A―)=1-P(A)

Ví dụ: Bài toán 01 Tính xác suất bằng quy tắc cộng

Phương pháp: Sử dụng các quy tắc đếm và công thức biến cố đối, công thức biến cố hợp.

– P(A ∪ B)=P(A)+P(B) với A và B là hai biến cố xung khắc

– P(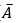)=1-P(A)

3.2. Quy tắc nhân xác suất:

Ta nói hai biến cố A và B độc lập nếu sự xảy ra (hay không xảy ra) của A không làm ảnh hưởng đến xác suất của B.

Hai biến cố A và B độc lập khi và chỉ khi P(A.B)=P(A).P(B)

Biến cố giao:

Cho hai biến cố A và B cùng liên quan đến một phép thử T. Biến cố “Cả A và B cùng xảy ra” được gọi là giao của hai biến cố A và B, kí hiệu là AB.

Nếu gọi ΩA là tập hợp mô tả các kết quả thuận lợi cho A, ΩB là tập hợp mô tả các kết quả thuận lợi cho B, thì tập hợp các kết quả thuận lợi cho AB là A∩B.

Tổng quát: Cho k biến cố A1,A2,…,Ak cùng liên quan đến một phép thử T. Biến cố “Tất cả k biến cố A1,A2,…,Ak đều xảy ra” được gọi là giao của k biến cố A1,A2,…,Ak, kí hiệu A1A2…Ak.

Biến cố độc lập:

Cho hai biến cố A và B cùng liên quan đến một phép thử T. Hai biến cố A và B được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng tới việc xảy ra hay không xảy ra của biến cố kia.

Nếu hai biến cố A, B độc lập với nhau thì A và B―, A― và B, A― và B― cũng độc lập với nhau.

Tổng quát: Cho k biến cố A1,A2,…,Ak cùng liên quan đến một phép thử T. k biến cố này được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của mỗi biến cố không làm ảnh hưởng tới việc xảy ra hay không xảy ra của các biến cố còn lại.

Ví dụ: Bài toán 02 Tính xác suất bằng quy tắc nhân

Phương pháp:

Để áp dụng quy tắc nhân ta cần Chứng tỏ A và B độc lập

Áp dụng công thức: P(A.B)=P(A).P(B)

4. Bài tập áp dụng các quy tắc tính xác suất:

Bài 1: Một con súc sắc không đồng chất sao cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, các mặt còn lại đồng khả năng. Tìm xác suất để xuất hiện một mặt chẵn

Hướng dẫn:

Ta sử dụng quy tắc cộng để giải bài toán

Gọi A_i là biến cố xuất hiện mặt i chấm (i=1,2,3,4,5,6)

Ta có P(A₁ )=P(A₂)=P(A₃ )=P(A₅ )=P(A₆ )=1/3 P(A₄ )=x

⇒ 5x + 3x = 1 ⇒ x = 1/8

Gọi A là biến cố xuất hiện mặt chẵn, suy ra A=A₂ ∪ A₄ ∪ A₆

Vì các biến cố xung khắc nên: P(A)=P(A₂)+P(A₄ )+P(A₆ )=1/8+3/8+1/8=5/8

Bài 2: Một hộp đựng 10 viên bi đỏ, 8 viên bi vàng và 6 viên bi xanh. Lấy ngẫu nhiên 4
viên bi. Tính xác suất để các viên bi lấy được đủ cả 3 màu.

Hướng dẫn:

Tổng số viên bi trong hộp là 24. Gọi Ω là không gian mẫu.

Lấy ngẫu nhiên 4 viên trong hộp ta có C 4cách lấy hay n( Ω ) = C 4 .

Gọi A là biến cố lấy được các viên bi có đủ cả 3 màu. Ta có các trường hợp sau:

– 2 bi đỏ, 1 bi vàng và 1 bi xanh: có C 2 C1C1 = 2160 cách

– 1 bi đỏ, 2 bi vàng và 1 bi xanh: có C1 C 2C1 = 1680 cách

– 1 bi đỏ, 1 bi vàng và 2 bi xanh: có C1 C1C 2 = 1200cách

Do đó, n(A) = 5040

Vậy, xác suất biến cố A là: P( A) = n( A) = 5040, n(Ω) 10626≈ 47, 4%.

Bài 3: Gọi M là tập hợp các số tự nhiên gồm 9 chữ số khác nhau. Chọn ngẫu nhiên một
số từ M, tính xác suất để số được chọn có đúng 4 chữ số lẻ và chữ số 0 đứng giữa hai chữ
số lẻ (các chữ số liền trước và liền sau của chữ số 0 là các chữ số lẻ).

Hướng dẫn:

Xét các số có 9 chữ số khác nhau:

– Có 9 cách chọn chữ số ở vị trí đầu tiên.

– Có 8 cách chọn 8 chữ số tiếp theo

Do đó số các số có 9 chữ số khác nhau là: 9. A8 = 3265920

Xét các số thỏa mãn đề bài:

– Có C 4 cách chọn 4 chữ số lẻ.

– Đầu tiên ta xếp vị trí cho chữ số 0, do chữ số 0 không thể đứng đầu và cuối nên có 7
cách xếp.

– Tiếp theo ta có2 cách chọn và xếp hai chữ số lẻ đứng hai bên chữ số 0.

– Cuối cùng ta có 6! cách xếp 6 chữ số còn lại vào 6 vị trí còn lại.

Gọi A là biến cố đã cho, khi đó n( A) = C 4 .7.A2 .6!= 302400.5 4

Vậy xác suất cần tìm làP( A) = 302400 = 5 .