Dưới đây là bài viết về chủ đề: Các dạng dài tập Toán hình học nâng cao lớp 5 có đáp án để giúp các em học sinh ôn luyện và nâng cao kiến thức với các dạng bài đã học về các hình nhưu hình tròn, hình thang..., mời bạn đọc theo dõi.
Mục lục bài viết
1. Các bài toán về nhận dạng các hình:
Bài 1: Cho tam giác ABC. Trên cạnh BC ta lấy 6 điểm. Nối đỉnh A với mỗi điểm vừa chọn. Hỏi đếm được bao nhiêu hình tam giác.
Giải:
Ta nhận xét :
– Khi lấy 1 điểm thì tạo thành 2 tam giác đơn ABD và ADC. Số tam giác đếm được là 3 : ABC, ADB và ADC. Ta có : 1 + 2 = 3 (tam giác)
– Khi lấy 2 điểm thì tạo thành 3 tam giác đơn và số tam giác đếm được là 6 : ABC, ABD, ADE, ABE, ADC và AEC. Ta có : 1+ 2 + 3 = 6 (tam giác)
Vậy khi lấy 6 điểm ta sẽ có 7 tam giác đơn được tạo thành và số tam giác đếm được là : 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (tam giác)
Cách 2:
– Nối A với mỗi điểm D, E, …, C ta được một tam giác có cạnh AD. Có 6 điểm như vậy nên có 6 tam giác chung cạnh AD (không kể tam giác ADB vì đã tính rồi)
– Lập luận tương tự như trên theo thứ tự ta có 5, 4, 3, 2, 1 tam giác chung cạnh AE, AP, …, AI.
– Vậy số tam giác tạo thành là :
7 + 6 + 5 + 4 +3 +2 + 1 = 28 (tam giác).
Bài 2: Cho hình chữ nhật ABCD. Chia mỗi cạnh AD và BC thành 4 phần bằng nhau, AB và CD thành 3 phần bằng nhau, rồi nối các điểm chia như hình vẽ.
Ta đếm được bao nhiêu hình chữ nhật trên hình vẽ?
Giải :
– Trước hết Ta xét các hình chữ nhật tạo bởi hai đoạn AD, EP và các đoạn nối các điểm trên hai cạnh AD và BC. Bằng cách tương tự như tronh ví dụ 1 ta tính được 10 hình.
– Tương tự ta tính được số hình chữ nhật tạo thành do hai đoạn EP và MN, do MN và BC đều bằng 10.
– Tiếp theo ta tính số hình chữ nhật tạo thành do hai đoạn AD và MN, EP và BC với các đoạn nối các điểm trên hai cạnh AD và BC đều bằng 10.
Vì vậy :
Số hình chữ nhật đếm được trên hình vẽ là :
10 + 10 + 10 + 10 + 10 + 10 = 60 (hình)
Đáp số 60 hình.
Bài 3: Cần ít nhất bao nhiêu điểm để khi nối lại ta được 5 hình tứ giác ?
Giải:
– Nếu ta chỉ có 4 điểm ( trong đó không có 3 điểm nào cùng nằm trên 1 đoạn thẳng) thì nối lại chỉ được 1 hình tứ giác.
– Nếu ta chọn 5 điểm, chẳng hạn A, B, C, D, E (trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng) thì :
+ Nếu ta chọn A là 1 đỉnh thì khi chọn thêm 3 trong số 4 điểm còn lại B, C, D, E và nối lại ta sẽ được một tứ giác có một đỉnh là A. Có 4 cách chọn 3 điểm trong số 4 điểm B, C, D, E để ghép với A. Vậy có 4 tứ giác đỉnh A.
– Có 1 tứ giác không nhận A làm đỉnh, dó là BCDE. Từ kết quả trên đây ta suy ra
Khi có 5 điểm ta được 5 tứ giác.
Vậy để có 5 hình tứ giác ta cần ít nhất 5 điểm khác nhau (trong đó không có 3 điểm nào nằm trên cùng một đoạn thẳng)
2. Các bài toán về diện tích các hình:
Kiến thức cần nhớ.
– Hình tam giác có 3 cạnh, 3 đỉnh. Đỉnh là điểm 2 cạnh tiếp giáp nhau. Cả 3 cạnh đều có thể lấy làm đáy.
– Chiều cao của hình tam giác là đoạn thẳng hạ từ đỉnh xuống đắy và vuông góc với đắy. Như vậy mỗi tam giác có 3 chiều cao.
Công thức tính :
– Hai tam giác có diện tích bằng nhau khi chúng có đáy bằng nhau (hoặc đáy chung), chiều cao bằng nhau (hoặc chung chiều cao).
– Hai tam giác có diện tích bằng nhau thì chiều cao của 2 tam giác ứng với 2 cạnh đắy bằng nhau đó cũng bằng nhau.
Hai tam giác có diện tích bằng nhau khi đáy tam giác P gấp đáy tam giác Q gấp chiều cao tam giác P bấy nhiêu lần.
Bài tập ứng dụng
Bài 1 : Cho tam giác ABC có diện tích là 150 cm2. Nếu kéo dài đáy BC (về phía B) 5 cm thì diện tích sẽ tăng thêm 37,5 cm2 . Tính đáy BC của tam giác.
Giải:
Cách 1 : Từ A kẻ đường cao AH của ∆ ABC thì AH cũng là đường cao của ∆ ABD
Đường cao AH là :
37,5 x 2 : 5 = 15 (cm)
Đáy BC là :
150 x 2 : 15 = 20 (cm)
Đáp số 20 cm.
Cách 2 :
Từ A hạ đường cao AH vuông góc với BC . Đường cao AH là đường cao chung của hai tam giác ABC và ABD . Mà : Tỉ số 2 diện tích tam giác là :
Hai tam giác có tỉ số diện tích là 4 mà chúng có chung đường cao,nên tỉ số 2 đáy cũng là 4. Với đáy BC là :
5 x 4 = 20 (cm)
Đáp số 20 cm.
Bài 2: Cho tam giác ABC vuông ở A có cạnh AB dài 24 cm, cạnh AC dài 32 cm. Điểm M nằm trên cạnh AC. Từ M kẻ đường song song với cạnh AB cắt BC tại N. Đoạn MN dài 16 cm. Tính đoạn MA.
Giải :
Diện tích tam giác NCA là
32 x 16 : 2 = 256 (cm2)
Diện tích tam giác ABC là :
24 x 32 : 2 = 348 (cm2)
384 – 256 = 128 (cm2)
Chiều cao NK hạ từ N xuống AB là : 128 x 2 : 24 = 10 ⅔ (cm)
Vì MN || AB nên tứ giác MNBA là hình thang vuông. Do vậy MA cũng bằng 10 ⅔cm
Đáp số: 10 ⅔ cm
Bài 3: Cho tam giác ABC vuông ở A. Cạnh AB dài 28 cm, cạnh AC dài 36 cm M là một điểm trên AC và cách A là 9 cm. Từ M kẻ đường song song với AB và đường này cắt cạnh BC tại N. Tính đoạn MN.
Giải:
Vì MN || AB nên MN ⊥ AC tại M. Tứ giác MNAB là hình
thang vuông. Nối NA. Từ N hạ NH⊥ AB thì NH là chiều cao của tam giác NBA và của hình thang MNBA nên NH = MA và là 9 cm.
Diện tích tam giác NBA là :
28 x 9 : 2 = 126 (cm2)
Diện tích tam giác ABC là :
36 x 28 : 2 = 504 (cm2)
Diện tích tam giác NAC là :
504 – 126 = 378 (cm2)
Đoạn MN dài là :
378 x 2 : 36 = 21 (cm)
3. Hình thang:
Bài 1: Cho hình thang ABCD có đáy nhỏ AB là 27 cm, đáy lớn CD là 48 cm. Nếu kéo dài đáy nhỏ thêm 5 cm thì diện tích của hình tăng 40 cm2. Tính diện tích hình thang đã cho.
Lời giải
Cách 1
Tam giác CBE có : Đáy BE = 5cm, chiều cao là chiều cao của hình thang ABCD
Vậy chiều cao của hình thang ABCD là : 40x 2 : 5 = 16 (cm)
Diện tích hình thang ABCD là : (27+48) x 16 : 2 = 600(cm2)
Cách 2
Tổng hai đáy hình thang gấp đáy BE là : (27 + 48) : 5 = 15 (lần)
Hai hình (thang và tam giác) có chiều cao chung nên diện tích hình thang gấp 15 lần diện tích ∆ BCE
Diện tích tam giác BCE là : 40 x 15 = 600 (cm2)
Bài 2 : Một thửa ruộng hình thang có diện tích là 361,8 m2. Đáy lớn hơn đáy nhỏ là 13,5 m. Hãy tính độ dài của mỗi đáy, biết rằng nếu tăng đáy lớn thêm 5,6 m thì diện tích thửa ruộng sẽ tăng thêm 3,6 m2.
Lời Giải :
Chiều cao của hình thang là :
33,6 x 2 : 5,6 = 12 (m)
Tổng hai đáy hình thang là :
361,8 x2 : 12 = 60,3 (m)
đáy nhỏ của hình thang là :
(60,3 – 13,5) : 2 = 23,4 (m)
Đáy lớn của hình thang là :
23,4 + 13,5 = 36,9 (m).
Bài 3 : Cho hình thang ABCD có đáy lớn CD là 20 cm, đáy nhỏ AB là 15 cm. M là một điểm trên AB cách B là 5 cm. Nối M với C. Tính diện tích hình thang mới AMCD. Biết diện tích tam giác MBC là 280 cm2.
Giải :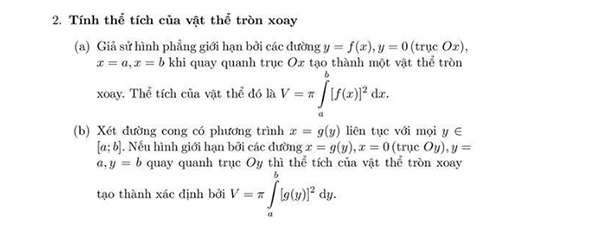
Cách 1
Đáy mới AM là :
15 – 5 = 10 (cm)
Tổng hai đáy AM và CD là :
10 + 20 = 30 (cm)
Chiều cao hình thang ABCD là :
280 x 2 : 5 = 112 (cm)
Diện tích hình thang ABCD là :
30 x 112 : 2 = 1680 (cm2)
Cách 2
Nối A với C
Ta có đoạn AM là : 15 – 5 = 10 (cm)
Diện tích tam giác ACM gấp 2 lần điện tích tam giác MCB Þ Diện tích tam giác ACM = 280 x 2 = 560 (cm2) (vì AM gấp BM hai lần và đường cao hai tam giác bằng nhau)
∆ DAC và ∆ MCB có :
DC gấp MB là: 20 : 5 = 4 ( lần)
Đường cao chung nên diện tích tam giác DAC gấp diện tích tam giác MCB 4 lần.
Diện tích tam giác ADC là :
280 x 4 = 1120 (cm2)
4. Các bài toán về cắt ghép hình:
Bài 1 : Hãy chia một hình chữ nhật thành 4 hình tam giác có diện tích bằng nhau ?
Lời Giải :
Xuất phát từ nhận xét :
– Hai tam giác có cùng chiều cao và số đo của đáy bằng nhau thì bằng nhau.
– Hai tam giác có chung đáy và số đo của đường cao bằng nhau thì diện tích bằng nhau.
Ta giải bài toán trên .
Trước hết ta kẻ đường chéo AC để hình chữ nhật thành hai tam giác códiện tích bằng nhau.
Bây giờ ta chia mỗi tam giác ABC và ADC thành hai tam giác có diện tích bằng nhau. Như vậy ta được một lời giải của bài toán.
Cách 1
Chọn AC làm đáy chung của 2 tam giác bằng nhau có cùng đường cao hạ từ B (và từ D) xuống AC thì phải chia đáy AC thành 2 phần bằng nhau bởi điểm O. Nối BO và DO ta được các tam giác ABO, BOC, COD và DOA thoả mãn các điều kiện của đề bài.
Cách 2
Chọn 2 cạnh BC và AD làm đáy của 2 tam giác sẽ chia ra. Như vậy các tam giác được chia ra từ tam giác ABC có chung đường cao AB cho nên ta phải chia đáy BC thành 2 phần có số đo bằng nhau bởi điểm M.Tương tự chia AD bởi điểm N. Nối AM, CN ta được 4 tam giác ABM, AMC, CAN và CND thoả mãn điều kiện của đề bài

Cách 3
Chọn hai cạnh AB và CD làm đáy của tam giác sẽ chia ra. Như vậy các tam giác được chia từ tam giác ABC có chung đường cao CB thành 2 phần có số đo bằng nhau bởi điểm P. Tương tự ta chia CD thành 2 phần bởi điểm H. Nối CP và AH ta được 4 tam giác ACP, CPB, ADH, và AHC thoả mãn điều kiện đề bài.

5. Hình tròn:
Bài 1 : Tìm diện tích hình vuông biết diện tích hình tròn là 50,24 cm2.
Lời giải: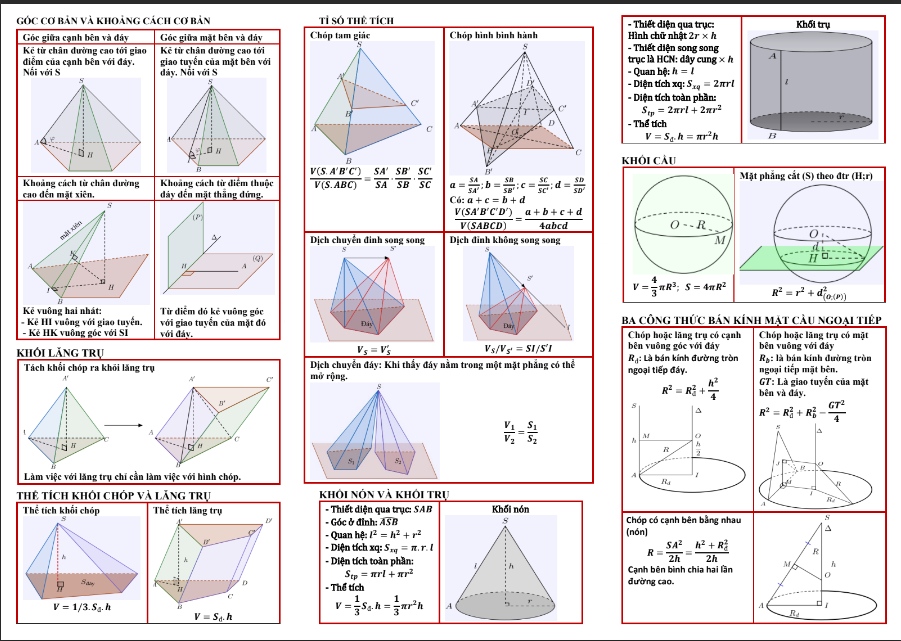
Gọi r là bán kính của hình tròn
Diện tích của hình tròn là :
r x r x 3,14
Theo bài ra ta có :
r x r x 3,14 = 50,24
r x r = 16
r x r = 4 x 4
Þ r = 4
Số đo đoạn thẳng BD là : 4 x 2 = 8 (cm)
Diện tích tam giác ABD là : (8×4)/2=16cm2
Diện tích hình vuông ABCD là : 16 x 2 = 32 (cm2)
Bài 2 : Hình tròn A có chu vi 219,8 cm, hình tròn B có diện tích 113,04 cm2. Hình tròn nào có bán kính lớn hơn?
Lời Giải :
Bán kính hình tròn A là :
219,8 : 3,14 : 2 = 35 (cm) = 3,5 dm.
Gọi r là bán kính hình tròn B ta có :
r x r = 113,04 : 3,14 = 36 (dm)
=> r = 6 dm
Vì 6 > 3,5 nên bán kính hình tròn B lớn hơn bán kính hình tròn A
6. Diện tích xung quanh, diện tích toàn phần, thể tích hình hộp chữ nhật, hình lập phương , hình trụ:
Bài 1 : Có 27 hình lập phương, mỗi hình có thể tích 8 cm3. Xếp 27 hình đó thành một hình lập phương lớn. hỏi hình lập phương lớn có cạnh là bao nhiêu?
Lời Giải :
Ta có : 8 = 2 x 2 x 2
Vậy mỗi hình lập phương nhỏ có đáy bằng 2 cm.
Xếp 27 hình lập phương nhỏ thành một hình lập phương lớn có 3 tầng mỗi tầng có 3 hàng, mỗi hàng có 3 hình lập phương nhỏ.
Nên cạnh của hình lập phương lớn là : 2 x 3 = 6 (cm)
Đáp số 6 cm
Bài 2 : Có 8 hình lập phương, mỗi hình có cạnh bằng 2 cm. Xếp 8 hình đó thành 1 hình lập phương lớn. Tìm diện tích xung quanh, diện tích toàn phần và thể tích của hình lập phương lớn.
Lời Giải :
8 hình lập phương ta xếp thành hình lập phương lớn bao gồm có 2 tầng mỗi tầng có 4 hình lập phương nhỏ
Cạnh của hình lập phương nhỏ là 2 nên cạnh của hình lập phương lớn là :
2 x 2 = 4 (cm)
Diện tích xung quanh là :
4 x 4 x 4 = 64 (cm2)
Diện tích toàn phần là :
4 x 4 x 6 = 96 (cm2)
Thể tích là :
4 x 4 x 4 = 64 (cm2)
Bài 3 : Một phiến đá hình hộp chữ nhật có chu vi đáy bằng 60 dm, chiều dài bằng 3/2 chiều rộng và chiều cao bằng 1/2 chiều dài. Phiến đá cân nặng 4471,2 kg. Hỏi 1 dm3 đá nặng bao nhiêu ki lô gam?
Lời Giải :
Nửa chu vi phiến đá là :
60 : 2 = 30 (dm)
Chiều dài của phiến đá là :
30 : (3 + 2) x 3 = 18 (dm)
Chiều rộng của phiến đá là :
30 – 18 = 12 (dm)
Chiều cao của phiến đá là :
18 : 2 = 9 (dm)
Thể tích của phiến đá là :
18 x 12 x 9 = 1944 (dm3)
1 dm3 đá nặng là :
4471,2 : 1944 = 2,3 (kg)
đáp số 2,3 kg
Bài 4 : Xếp 8 hình lập phương nhỏ có cạnh 4 cm thành một hình lập phương lớn rồi sơn tất cả các cạnh của hình lập phương lớn. Hỏi mỗi hình lập phương nhỏ có mấy mặt được sơn và diện tích được sơn của mỗi HLP nhỏ là bao nhiêu?
Lời Giải :
Xếp 8 HLP nhỏ thành 1 HLP lớn gồm 2 tầng, mỗi tầng gồm 4 hình lập phương nhỏ, vì thế mỗi HLP nhỏ đều có 3 mặt được ghép với các hình lập phương khác. Các mặt được ghép không được sơn. Vì HLP có 6 mặt nên số mặt được sơn là :
6 – 3 = 3 (mặt)
Diện tích một mặt của HLP nhỏ là :
4 x 4 = 16 (cm2)
Diện tích mỗi HLP nhỏ được sơn là :
16 x 3 = 48 (cm2)
Đáp số 48 cm2




