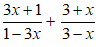Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 9 là tài liệu tham khảo để đáp ứng nhu cầu của giáo viên trong việc bồi dưỡng học sinh khá, giỏi môn Toán lớp 9 và các bạn có nhu cầu được tiếp xúc, rèn luyện với những dạng đề thi cơ bản và nâng cao.
Mục lục bài viết
1. Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 9 hay:
Bài 1: (6,0 điểm)
1) Cho biểu thức 
a/ Tìm điều kiện của Q và rút gọn Q
b/ Tính giá trị của Q khi ![]()
2) Chứng minh rằng A = 13 + 23 + 33 + …+ 1003 chia hết cho B = 1 + 2 + 3 + … + 100
Bài 2: (4,0 điểm)
1) Giải phương trình: ![]()
2) Cho abc = 1.Tính S = ![]()
Bài 3: (3,0 điểm)
1) Tìm nghiệm nguyên của phương trình: x2 + 2y2 + 2xy + 3y – 4 = 0
2) Biết rằng a,b là các số thoả mãn a > b > 0 và a.b = 1 Chứng minh : 
Bài 3: (6,0 điểm)
Cho nửa đường tròn đường kính BC = 2R, tâm O cố định. Điểm A di động trên nửa đường tròn. Gọi H là hình chiếu của điểm A lên BC. Gọi D và E lần lượt là hình chiếu của H lên AC và AB.
a) Chứng minh tam giác ABC vuông
b) Chứng minh: AB . EB + AC . EH = AB2
c) Xác định tam giác ABC sao cho tứ giác AEHD có diện tích lớn nhất? Tính d/ tích lớn nhất đó theo R.
Bài 5: (1,0 điểm)
Tìm nghiệm nguyên dương của phương trình: 2(x+y)+16=3xy
ĐÁP ÁN
| Bài | Tóm tắt lời giải | Điểm |
| Bài 1 Câu 1a (2đ) |
| 0,5
0,5
0,5
0,5 |
| Bài 1 Câu 1b (2 đ) |
| 0,5
0,5
0,5
0,5 |
| Bài 1 Câu 2 (2 đ) | 2. Ta có: B = (1 + 100) + (2 + 99) + …+ (50 + 51) = 101. 50 Để chứng minh A chia hết cho B ta chứng minh A chia hết cho 50 và 101 Ta có: A = (13 + 1003) + (23 + 993) + … +(503 + 513) = (1 + 100)(12 + 100 + 1002) + (2 + 99)(22 + 2. 99 + 992) + … + (50 + 51)(502 + 50. 51 + 512) = 101(12 + 100 + 1002 + 22 + 2. 99 + 992 + … + 502 + 50. 51 + 512) chia hết cho 101 (1) Lại có: A = (13 + 993) + (23 + 983) + … + (503 + 1003) Mỗi số hạng trong ngoặc đều chia hết cho 50 nên A chia hết cho 50 (2) Từ (1) và (2) suy ra A chia hết cho 101 và 50 nên A chi hết cho B | 0,5 0,25
0,25 0,25 0,25
0,25 0,25 0,25 |
| Bài 2 (1,5 đ) | 1. | 0,5
1,0 |
| (2,5 đ) | 2. Cho abc = 1. | 0.5
0,5
0,5
0,5
0,5 |
| Bài 3
(1,5đ) |
x2 + 2y2 + 2xy + 3y – 4 = 0 (1) | |
| (1) | 0,25 | |
| | 0,25 | |
| | 0,25 | |
|
| 0,25 | |
| Vì y nguyên nên | 0,25 | |
| Thay các giá trị nguyên của y vào (2) ta tìm được các cặp nghiệm nguyên (x; y) của PT đã cho là: (4; -4), (1; -3), (5; -3), ( -2; 0), (-1; 1). | 0,25 | |
| (1,5 đ) | 2. – Vì a.b = 1 nên
– Do a > b > 0 nên áp dụng BĐT Cô Si cho 2 số dương Ta có : Vậy | 0,25
0,25
0,25
0,5
0,25 |
| Bài 4 6đ |  | 0,5
|
| a) Chứng minh tam giác ABC vuông Ta có: OA= OB = OC = R => Tam giác ABC vuông tại A (theo đl đảo) | 0,25 0,25
| |
| b) Chứng minh: AB . EB + AC . EH = AB2 Chứng minh tứ giác ADHE là hình chữ nhật AB . EB = HB2 AC . EH = AC . AD = AH2 Ta có: AB2 = AH2 + HB2 (định lý Pi ta go) => Đpcm | 0,5 0,5 0,5 0,5 0,5 | |
|
<=> Tam giác ABC vuông cân tại A | 1,0
0,5 0,5 0,5 | |
| Bài 5 (1,0đ) |
=> nghiệm nguyên dương của PT là: ( 1; 18);( 18; 1); ( 2; 5); ( 5; 2) | 0,25
0,25
0,25
0,25 |
2. Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 9 chi tiết:
Bài 1: (3,5 điểm)
Chứng minh rằng với mọi số tự nhiên n ta có:
A = 7.52n + 12.6n chia hết cho 19
Bài 2: (2,5 điểm)
Tìm số tự nhiên n sao cho: n + 24 và n – 65 là hai số chính phương
Bài 3: (3,0 điểm)
Cho a, b > 0 và a + b = 1.
Chứng minh rằng : ![]()
Bài 4: (3,0 điểm)
Cho x, y là hai số dương thỏa mãn : x2 + y2 = 4.
Tìm giá trị nhỏ nhất của biểu thức : 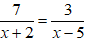
Bài 5: (4,0 điểm)
Cho tam giác ABC có D là trung điểm cạnh BC, điểm M nằm trên trung tuyến AD. Gọi I, K lần lượt là các trung điểm tương ứng của MB, MC và P, Q là các giao điểm tương ứng của các tia DI, DK với các cạnh AB, AC.
Chứng minh: PQ // IK.
Bài 6: (4,0 điểm)
Cho tam giác ABC có BC = a , CA = b , AB = c. Gọi đường cao hạ từ các đỉnh A,B,C xuống các cạnh BC , CA và AB tương ứng là ha , hb , hc . Gọi O là một điểm bất kỳ trong tam giác đó và khoảng cách từ O xuống ba cạnh BC , CA và AB tương ứng là x , y và z .
Tính 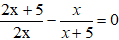
ĐÁP ÁN
| Bài 1 (3,5đ) | Với n = 0 ta có A(0) = 19 Giả sử A chia hết cho 19 với n = k nghĩa là: A(k) = 7.52k + 12.6k Ta phải chứng minh A chia hết cho 19 với n = k + 1 nghĩa là phải chứng minh: A(k + 1) = 7.52(k + 1) + 12.6k + 1 Ta có: A(k + 1) = 7.52(k + 1) + 12.6k + 1 = 7.52k.52 + 12.6n. 6 = 7.52k.6 + 7.52k .19 + 12.6n. 6 = 6.A(k) + 7.52k .19 Vậy theo nguyên lý quy nạp thì A = 7.52n + 12.6n chia hết cho 19 với mọi số tự nhiên n | 0,5 0,75 0,75
1,0 0,5 | |||||
| Bài 2 (2,5đ)
1 | Ta có:
| 0,5
0,5 0,5
0,5
0,5 | |||||
| Bài 3 (3,0đ) | Nhận xét rằng với mọi x,y ta có: Đặt Vì Do đó : | 0,5
0,5
0,75
0,5
0,75 | |||||
| Bài 4 (3,0đ) | Ta có Áp dụng BĐT: Ta có Áp dụng BĐT: Ta có Vậy giá trị nhỏ nhất của biểu thức E = 9 . Dấu “=” xảy ra khi x = y = | 0,5
1,0
1,0
0,5 | |||||
| Bài 5 (4,0đ) |
| – Vẽ hình đúng – Gọi E là trung điểm của AM, chứng minh được: IK // BC, EI // AB, EK // AC – Áp dụng định lý Ta-lét vào các tam giác DPA, DAQ. Suy ra:
– Áp dụng định lý Ta-lét đảo vào tam giác DPQ, suy ra: PQ // IK | 0,5
1,5
1,5
0,5 | ||||
| Bài 6 (4,0đ) | Vẽ hình đúng
| 0,5
0,5
1,0
0,5
0,5
1,0 | |||||
3. Các bài Toán, đề thi ôn luyện học sinh giỏi môn Toán lớp 9 đầy đủ:
Câu 1: (1 điểm)
Phân tích đa thức sau thành nhân tử : ![]()
Câu 2: (1 điểm)
Giải phương trình sau:
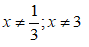
Câu 3: (2 điểm)
a/ Chứng minh rằng 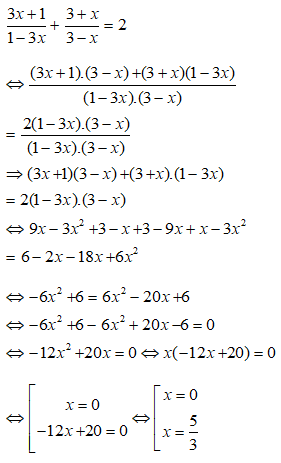
b/ Cho hai số dương a,b và a=5-b.
Tìm giá trị nhỏ nhất của tổng P=![]()
Câu 4:(2 điểm)
a/ Cho a và b là hai số thực dương thõa mãn điều kiện :
![]()
Hãy tính tổng: S=![]()
b/ Chứng minh rằng :A=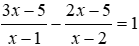 là số nguyên
là số nguyên
Câu 5: (1 điểm) Tìm các số nguyên dương x,y thõa mãn phương trình sau:
xy-2x-3y+1=0
Câu 6: (3điểm)
Cho tam giác ABC vuông tại A có cạnh AC>AB ,đường cao AH (H thuộc BC).Trên tia HC lấy điểm D sao cho HD=HA.Đường vuông góc với với BC tại D cắt AC tại E.
a) Chứng minh hai tam giác BEC và ADC đồng dạng
b) Chứng minh tam giác ABE cân.
c) Gọi M là trung điểm của BE và vẽ tia AM cắt BC tại G. Chứng minh rằng: ![]()
ĐÁP ÁN
Câu 1: (1 điểm)
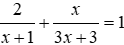
Câu 2: ( 1 điểm)
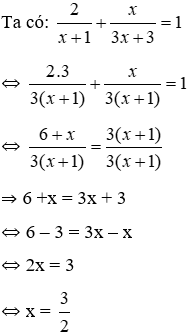
Câu 3: (2 điểm)
a/ (1 điểm)
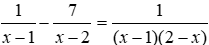
b/ (1 điểm)
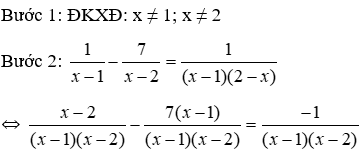
Câu 4 (2 điểm)
a/ (1 điểm)
Ta có:
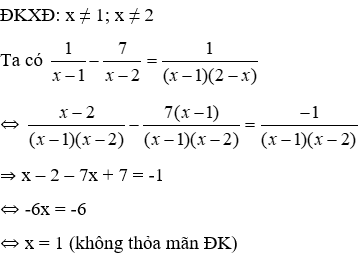
Vậy S=1+1=2
b/ (1 điểm)
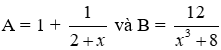
Câu 5 (1 điểm)
xy-2x-3y+1=0
xy-3y=2x-1
y(x-3)=2x-1
Ta thấy x=3 không thõa mãn,với x![]() 3 thì
3 thì
y=2+![]()
Để y nguyên thì x-3 phải là ước của 5
Suy ra: (x,y) là (4,7) ;(8,3)
Câu 6 (3 điểm)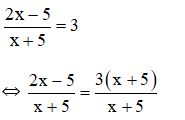
a) (1đ điểm)
Tam giác ADC và tam giác BEC:
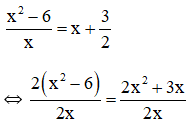 ( vì hai tam giác CDE và CAB đồng dạng)
( vì hai tam giác CDE và CAB đồng dạng)
Góc C: chung
Suy ra: Tam giác ADC đồng dạng với tam giác BEC (c-g-c)
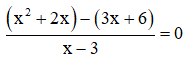
Do đó: Tam giác ABE cân( tam giác vuông có một góc bằng 45 độ)
c) (1 điểm)
Tam giác ABE cân tại E nên AM còn là phân giác của góc BAC
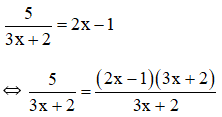






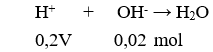
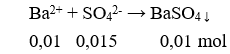

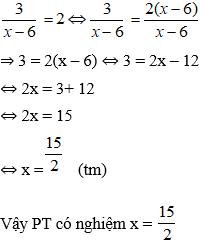

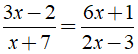
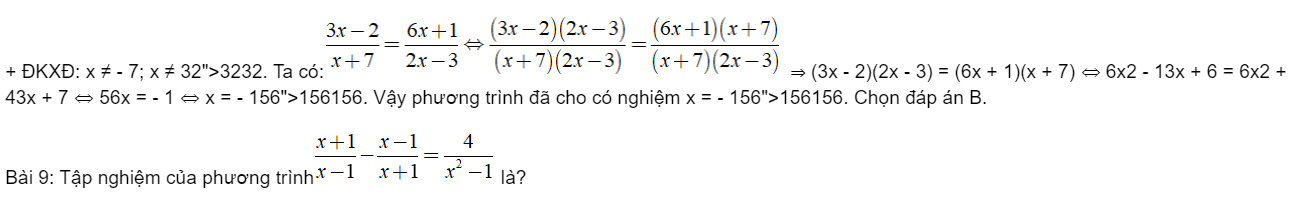
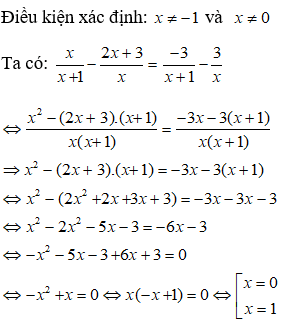 với a > 0; b > 0.
với a > 0; b > 0.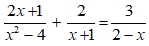
 Xét hai tam giác ABC và OBC ta có :
Xét hai tam giác ABC và OBC ta có :