Dưới đây là bảng công thức đạo hàm, đạo hàm lượng giác, các hàm lượng giác và công thức đạo hàm cao cấp đầy đủ nhất giúp các bạn dễ dàng ôn lại những kiến thức toán học về đạo hàm đã được học một cách nhanh nhất để giải bài tập nhanh hơn, hiệu quả hơn.
Mục lục bài viết
1. Đạo hàm là gì? Đạo hàm lượng giác là gì?
Đạo hàm là một khái niệm quan trọng trong toán học và giải tích, đặc biệt là trong lĩnh vực vi phân tích. Đạo hàm của một hàm số thể hiện tốc độ thay đổi của hàm số đó tại một điểm cụ thể. Nó mô tả mức độ biến thiên của hàm số tại điểm đó và cho biết xu hướng tăng hoặc giảm của hàm số.
Khi nói về đạo hàm của một hàm số f(x) tại một điểm x=c, chúng ta thường sử dụng ký hiệu f'(c) hoặc  để biểu diễn. Đạo hàm được định nghĩa là giới hạn của tỉ số
để biểu diễn. Đạo hàm được định nghĩa là giới hạn của tỉ số ![]() khi x tiến gần đến c, nếu giới hạn này tồn tại.
khi x tiến gần đến c, nếu giới hạn này tồn tại.
Việc tính đạo hàm là quá trình xác định hàm số đó có tỷ lệ biến thiên như thế nào tại một điểm cụ thể. Đạo hàm cho biết độ dốc của đồ thị hàm số tại điểm đó. Nếu đạo hàm dương tại một điểm, hàm số tăng dần tại điểm đó. Nếu đạo hàm âm, hàm số giảm dần. Nếu đạo hàm bằng 0, điều này thường chỉ ra điểm cực trị của hàm số.
Đạo hàm không chỉ quan trọng trong việc hiểu biểu diễn đồ thị của hàm số mà còn có nhiều ứng dụng thực tế rộng rãi. Nó được sử dụng trong các lĩnh vực như vật lý, kinh tế học, khoa học máy tính, và nhiều lĩnh vực khác để mô hình hóa và dự đoán các hiện tượng biến đổi theo thời gian.
Khái niệm về đạo hàm còn đi sâu vào các khái niệm khác như đạo hàm riêng, đạo hàm bậc cao, và ứng dụng của đạo hàm trong việc tìm kiếm cực trị, xác định đường tiếp tuyến, xác định vận tốc và gia tốc trong vật lý, và nhiều ứng dụng khác.
Từ việc hiểu sâu hơn về đạo hàm, chúng ta có thể áp dụng nó vào các bài toán thực tế và hiểu rõ hơn về sự biến đổi của các hàm số và tốc độ thay đổi của chúng tại các điểm cụ thể.
Đạo hàm lượng giác: Đạo hàm của các hàm lượng giác – các hàm gồm các hàm sin(x), cos(x), và các biến thể của chúng – là một phần quan trọng trong toán học và vật lý. Các hàm lượng giác thường xuyên xuất hiện trong nhiều vấn đề liên quan đến sóng, dao động, cơ học, điện tử và nhiều lĩnh vực khác.
Khi nói về đạo hàm của các hàm lượng giác, chúng ta thường áp dụng các quy tắc đạo hàm cơ bản như sau:
– Đạo hàm của hàm sin(x) là cos(x).
– Đạo hàm của hàm cos(x) là -sin(x).
– Đạo hàm của hàm csc(x) là -csc(x) * cot(x).
– Đạo hàm của hàm cot(x) là -csc^2(x).
Các quy tắc này giúp chúng ta tính được tốc độ thay đổi của các hàm lượng giác tại các điểm cụ thể. Ví dụ, khi áp dụng đạo hàm của hàm sin(x), chúng ta biết rằng tại một điểm x nào đó, đạo hàm của hàm sin(x) sẽ cho chúng ta biết tốc độ thay đổi của sin(x) tại điểm đó, tức là cos(x).
Đạo hàm của các hàm lượng giác không chỉ đơn thuần là quy tắc tính toán mà còn được áp dụng rộng rãi trong việc giải quyết các vấn đề thực tế. Ví dụ, trong vật lý, việc tính toán đạo hàm của các hàm lượng giác giúp xác định tốc độ, gia tốc và biến đổi của các quá trình dao động cơ học, sóng học và điện từ.
Các định lý và ứng dụng của đạo hàm lượng giác không chỉ giúp chúng ta hiểu rõ hơn về tính chất của các hàm số mà còn mở ra cánh cửa cho việc áp dụng toán học vào các vấn đề thực tế, từ việc thiết kế các mô hình trong công nghiệp đến việc dự đoán và điều khiển các hiện tượng tự nhiên.
2. Bảng đầy đủ các công thức đạo hàm và đạo hàm lượng giác:
Công thức đạo hàm cơ bản



Công thức đạo hàm lượng giác

Bảng đạo hàm

3. Bài tập về Đạo hàm và hướng dẫn giải:
Bài tập trắc nghiệm
Bài 1: Hàm số y = (1 + sinx)(1 + cosx) có đạo hàm là:
A. y’ = cosx – sinx + 1.
B. y’ = cosx + sinx + cos2x.
C. y’ = cosx – sinx + cos2x.
D. y’ = cosx + sinx + 1.
 Chọn đáp án C
Chọn đáp án CBài 2: Cho hàm số y = f(x) = sinx”> + cosx”>. Giá trị 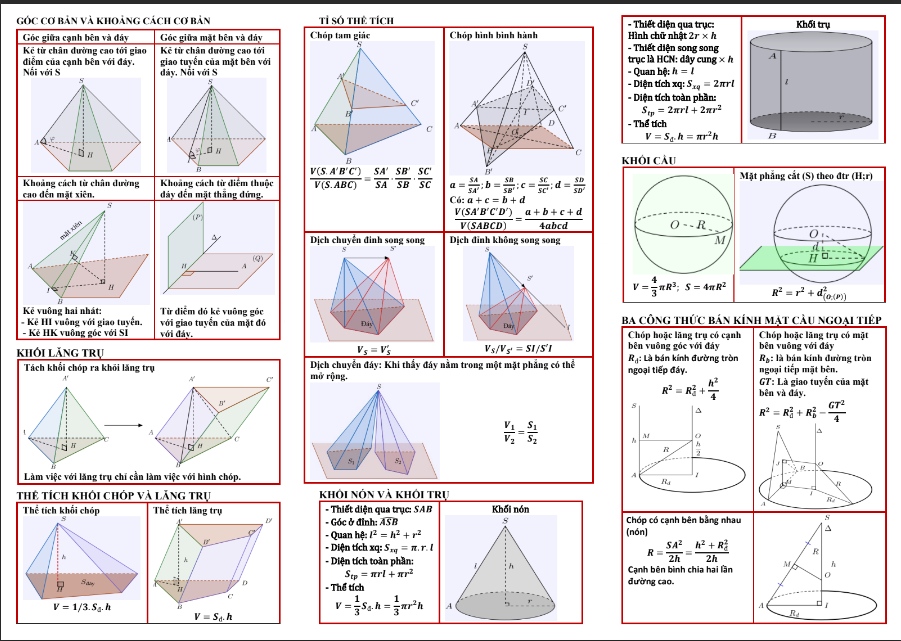 bằng:
bằng:

 Chọn đáp án A
Chọn đáp án A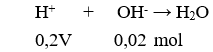
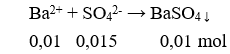 Chọn đáp án C
Chọn đáp án CBài 4: Cho hàm số 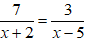 bằng:
bằng:
A.1
B. 12″>12.
C. 0
D. Không tồn tại.
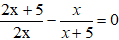 Chọn đáp án C
Chọn đáp án C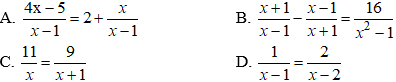
 Chọn đáp án C
Chọn đáp án C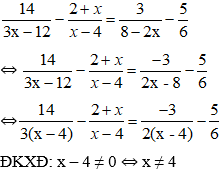
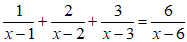 Chọn đáp án C
Chọn đáp án C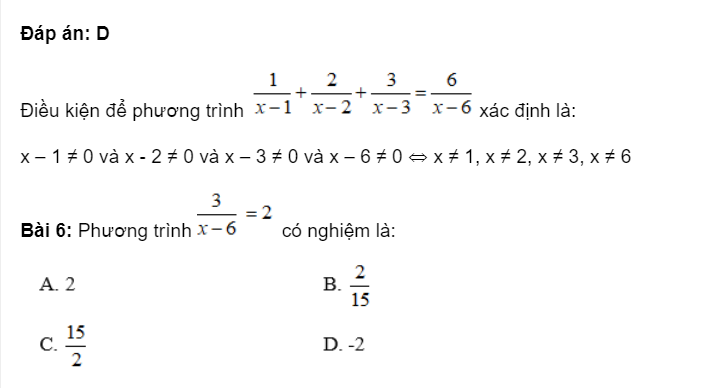
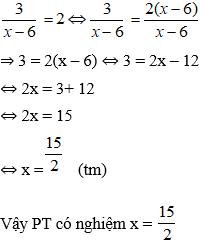 Chọn đáp án D
Chọn đáp án DBài 8: Cho hàm số ![]() . Khi đó nghiệm của phương trình là:
. Khi đó nghiệm của phương trình là:
A. π + k2π.
B. 2π + k4π.
C. 2π + kπ.
D. π + kπ.
 Chọn đáp án B
Chọn đáp án BBài 9: Hàm số 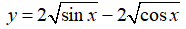 có đạo hàm là:
có đạo hàm là:
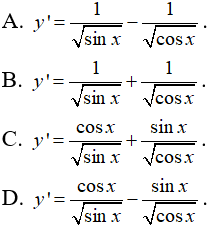
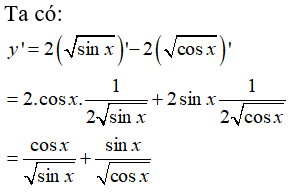 Chọn đáp án C
Chọn đáp án CBài 10: Tính đạo hàm của hàm số sau: y = 2sin24x – 3cos35x.
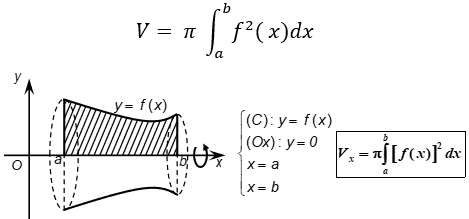
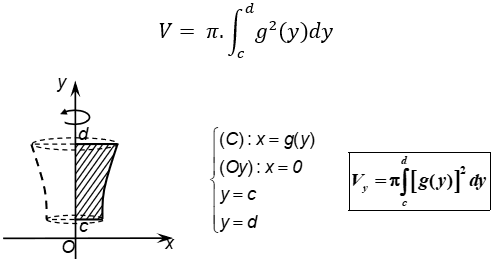
Bài 1: Tính đạo hàm của hàm số sau: y = (2 + sin22x)3.
Lời giải:
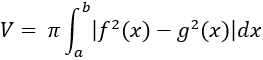
Bài 2: Đạo hàm của hàm số 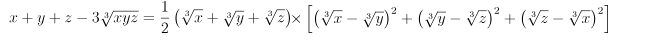 là
là
Lời giải:n
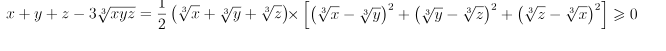
Bài 3: Đạo hàm của hàm số 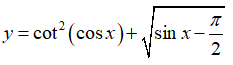 là
là
Lời giải:
Bài 4: Hàm số  có đạo hàm bằng:
có đạo hàm bằng:
Lời giải:
Bài 5: Tính đạo hàm của hàm số sau:  .
.
Lời giải:

Bài 6: Tính đạo hàm của hàm số sau: y = sin(cos2x.tan2x).
Lời giải:

Bài 7: Tính đạo hàm của hàm số sau: 
Lời giải:
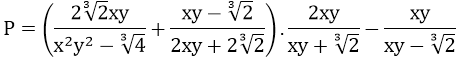
Bài 8: Tính đạo hàm của hàm số sau: y = sin2(cos(tan43x))
Lời giải:
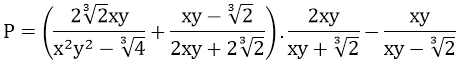
Bài 10:
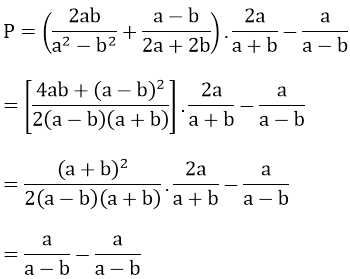
Lời giải:

Bài 10: Đạo hàm của hàm số
![]()
bằng biểu thức nào?
Lời giải:
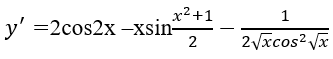
Bài tập vận dụng
Bài 1 Đạo hàm của hàm số
![]()
bằng biểu thức nào sau đây?
Bài 2 Tính đạo hàm của hàm số y = x.cosx.
Bài 3 Tính đạo hàm của hàm số sau: y = sin3(2x + 1) .
Bài 4 Tính đạo hàm của hàm số sau: ![]() .
.
Bài 5 Tính đạo hàm của hàm số sau: ![]() .
.
Bài 6 Hàm số 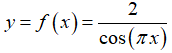 có f'(3) bằng?
có f'(3) bằng?
Bài 7 Cho hàm số y = cos3x.sin2x. Tính 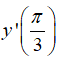
4. Bài tập về đạo hàm lượng giác:
Bài 1: Đạo hàm của hàm số:
![]() bằng bao nhiêu?
bằng bao nhiêu?
Hướng dẫn:
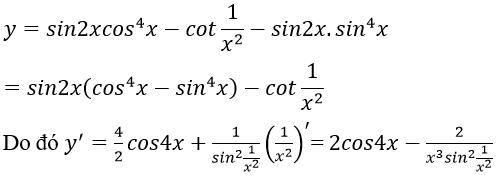
Bài 2: Tính đạo hàm của hàm số y = cos2x + cos4x + sin5x
Hướng dẫn:
Ta có: y’ = -2sin2x – 4sin4x + 5cos5x
Bài 3: Đạo hàm của hàm số y = √cosx bằng biểu thức nào?
Hướng dẫn:
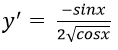
Bài 4: Đạo hàm của hàm số y = tan(2x+1) – xcos2x bằng biểu thức nào?
Hướng dẫn:
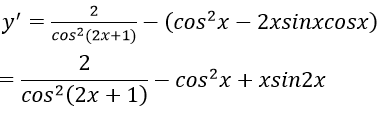
Bài 5: Đạo hàm của hàm số ![]() bằng biểu thức nào?
bằng biểu thức nào?
Hướng dẫn:
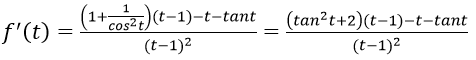
Bài 6: Đạo hàm của hàm số y = 6(sin4x + cos4x) – 4(sin6x + cos6x) bằng biểu thức nào?
Hướng dẫn:
y’ = 6(sin2x + cos2x)2 – 12sin2xcos2x – 4(sin2x + cos2x)2 + 12sin2xcos2x(sin2x + cos2x) = 2
Bài 7: Tính đạo hàm của hàm số: y = sinx.cosx
Hướng dẫn:
![]()
B. Bài tập vận dụng
Bài 1: ![]() bằng:
bằng:
A. 1 B. 0 C. 2/3 D. 3/2
Lời giải:
Đáp án: C
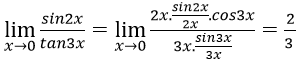
Đáp án C
Bài 2: Đạo hàm của hàm số:
![]() bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
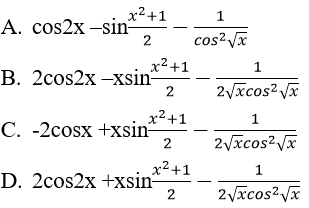
Lời giải:
Đáp án: B
![]()
Đáp án B
Bài 3: Đạo hàm của hàm số:
![]() bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
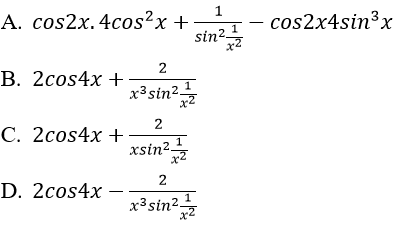
Lời giải:
Đáp án: D
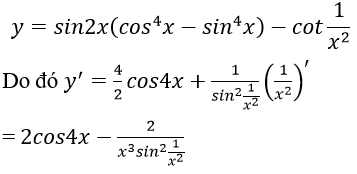
Đáp án D
Bài 4: Đạo hàm cuả hàm số:
![]() bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
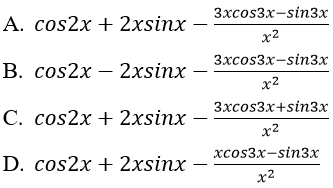
Lời giải:
Đáp án: B
![]()
Chọn đáp án B
Bài 5: Đạo hàm của hàm số:
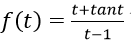 bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
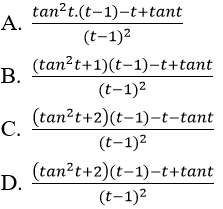
Lời giải:
Đáp án: C
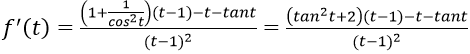
Chọn đáp án C
Bài 6: Đạo hàm của hàm số:
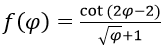 bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
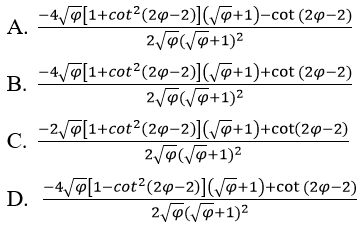
Lời giải:
Đáp án: A
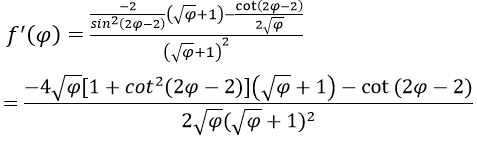
Chọn đáp án A
Bài 7: Đạo hàm của hàm số y = 6(sin4x + cos4x) – 4(sin6x + cos6x) bằng biểu thức nào sau đây?
A. 24(sin3x + cos3x) – 24(sin5x + cos5x)
B. 24(sin3x – cos3x) – 24(sin5x + cos5x)
C. 2
D. 0
Lời giải:
Đáp án: D
y’= 6(sin2x + cos2x)2 – 12sin2xcos2x – 4(sin2x + cos2x)2 + 12sin2xcos2x(sin2x + cos2x) = 2
Chọn đáp án D
Bài 8: Đạo hàm của hàm số y = √sinx bằng biểu thức nào sau đây:
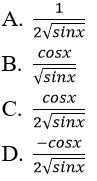
Lời giải:
Đáp án: C
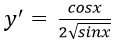
Chọn đáp án C
Bài 9: Cho hàm số f(x) = cos2x. Giá trị của f'(π/6) bằng:

Lời giải:
Đáp án: D
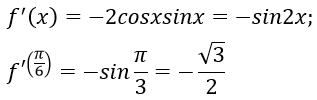
Chọn đáp án D
Bài 10: Đạo hàm của hàm số y = tan(2x+1) – xcos2x bằng biểu thức nào sau đây:
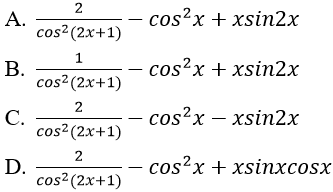
Lời giải:
Đáp án: A
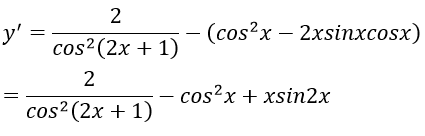
Chọn đáp án A
Bài 11: Đạo hàm của hàm số y = cot2x2 bằng biểu thức nào sau đây:
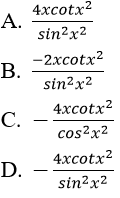
Lời giải:
Đáp án: D
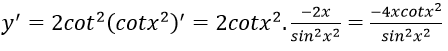
Chọn đáp án D
Bài 12: Cho hàm số f(x) = sin4x + cos4x – 2sin2x cos2x. Giá trị của f'(π/24) bằng:
A. -1
B. 1
C. 1/2
D. (-1)/2
Lời giải:
Đáp án: A
Bài 13: Đạo hàm cấp hai của hàm số y = cos2x bằng biểu thức nào sau đây?
A. -2sin2x
B. -4cos2x
C. -4sin2x
D. 4cos2x
Lời giải:
Đáp án: C
y’ = (cos2x)’= -4sin2x
Chọn đáp án C




