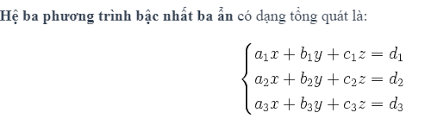Mục lục bài viết
1. Bài tập hệ phương trình bậc nhất hai ẩn có đáp án:
Câu 1: Cho phương trình ax + by = c với a ≠0, b ≠ 0 . Nghiệm của phương trình được biểu diễn bởi
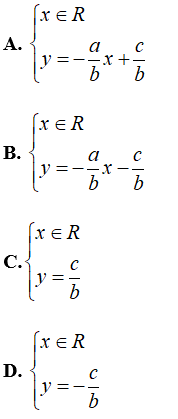
Lời giải:
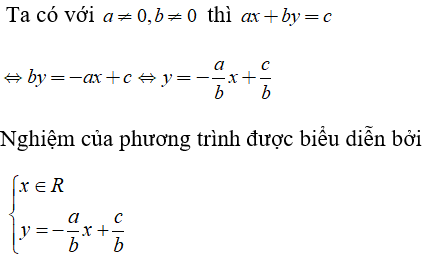
Chọn đáp án A
Câu 2: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
Lời giải:
Phương trình 
là phương trình bậc nhất hai ẩn
Chọn đáp án C
Câu 3: Phương trình nào dưới đây nhận cặp số (-2; 4) làm nghiệm
A. x – 2y = 0
B. 2x + y = 0
C. x – y = 0
D. x + 2y + 1 = 0
Lời giải:
Chọn đáp án B
Câu 4: Phương trình x – 5y + 7 = 0 nhận cặp số nào sau đây là nghiệm?
A. (0; 1)
B. (-1; 2)
C. (3; 2)
D. (2; 4)
Lời giải:
+ Thay x = 0; y = 1 vào phương trình x – 5y + 7 = 0 ta được 0 – 5.1 + 7 = 0 ⇔ 2 = 0 (vô lí) nên loại A
+ Thay x = -1; y = 2 vào phương trình x – 5y + 7 = 0 ta được -1 – 5.2 + 7 = 0 hay – 4 = 0 ⇒ (vô lí) nên loại B
+ Thay x = 2; y = 4 vào phương trình x – 5y + 7 = 0 ta được 2 – 5.4 + 7 = 0 ⇔ -11 = 0 (vô lí) nên loại D
+ Thay x = 3; y = 2 vào phương trình x – 5y + 7 = 0 ta được 3 – 5.2 + 7 = 0 ⇔ 0 = 0 (luôn đúng) nên chọn C
Chọn đáp án C
Câu 5: Tìm m để phương trình T 
nhận cặp số (1; 1) làm nghiệm
A. m = 5
B. m = 2
C. m = -5
D. m = -2
Lời giải:
Chọn đáp án A
Câu 6: Cho phương trình 2x – 4y + 10 = 0 . Tập nghiệm của phương trình trên được biểu diễn bởi đường thẳng ?
Lời giải:
Chọn đáp án A.
Câu 7: Cho phương trình 2x – 6 = 0. Đường thẳng biểu diễn tập nghiệm của phương trình trên là đường thẳng?
A. Song song trục hoành
B. Song song trục tung.
C. Song song đường thẳng x – 3 = 0
D. Trùng với đường thẳng 3x + 9 = 0
Lời giải:
Ta có: 2x – 6 = 0 ⇔ 2x = 6 ⇔ x = 3 Do đó, đường thẳng biểu diễn tập nghiệm phương trình đã cho là đường thẳng song song trục tung Oy.
Chọn đáp án B.
Câu 8: Cho phương trình: 
Đường thẳng biểu diễn tập nghiệm của phương trình trên là đường thẳng :
A. Song song đường thẳng
B. Song song trục tung.
C. Song song trục hoành.
D. Song song với đường thẳng
Lời giải:
Ta có:
Do đó, đường thẳng biểu diễn tập nghiệm của phương trình đã cho là đường thẳng song song trục hoành.
Chọn đáp án C.
Câu 9: Cho phương trình : 3x – y = 9. Nghiệm tổng quát của phương trình là:
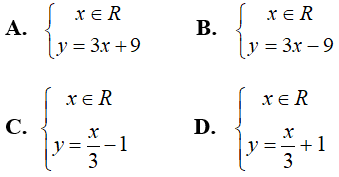
Lời giải:
Ta có: Do đó, nghiệm tổng quát của phương trình đã cho là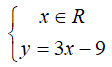 
Chọn đáp án B.
Câu 10: Cho phương trình: 5x – 10y = 25. Tìm nghiệm tổng quát của phương trình đã cho?
Lời giải:
Chọn đáp án C.
Câu 11: Tìm tất cả nghiệm nguyên của phương trình 5x – 3y = 8
Lời giải:
Đáp án cần chọn là: A
Câu 12: Tìm nghiệm nguyên âm lớn nhất của phương trình −5x + 2y = 7
A. (−7; −14)
B. (−1; −2)
C. (−3; −4)
D. (−5; −9)
Lời giải:
Đáp án cần chọn là: C
Câu 13: Tìm nghiệm nguyên âm của phương trình 3x + 4y = −10 là (x; y). Tính x.y
A. 2
B. −2
C. 6
D. 4
Lời giải:
Hay nghiệm nguyên của phương trình 3x + 4y = −10 là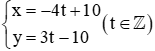 
Vì x; y nguyên âm hay x < 0; y < 0 nên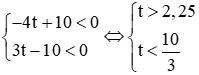 
mà t ∈ Z ⇒ t = 3
Suy ra x = −4.3 + 10 = −2; y = 3.3 – 10 = −1 nên nghiệm nguyên âm cần tìm là (a; y) = (−2; −1) ⇒ x.y = 2
Đáp án cần chọn là: A
Câu 14: Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình −4x + 3y = 8. Tính x + y
A. 5
B. 6
C. 7
D. 4
Lời giải:
Nghiệm nguyên dương nhỏ nhất của phương trình là 
⇒ x + y = 5
Đáp án cần chọn là: A
Câu 15: Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình 6x − 7y = 5. Tính x – y
A. 2
B. 3
C. 1
D. −1
Lời giải:
Do đó nghiệm nguyên dương nhỏ nhất của phương trình có được khi t = 1
Đáp án cần chọn là: C
2. Cách giải bài tập hệ phương trình bậc nhất hai ẩn:
Dạng 1: Giải hệ phương trình bằng phương pháp thế
Phương pháp giải: Để giải một hệ phương trình, ta sẽ biến đổi hệ đã cho thành hệ phương trình tương đương đơn giản hơn.
Để giải phương trình bằng phương pháp thế ta sử dụng quy tắc thế sau:
Bước 1: Từ một phương trình của hệ phương trình đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy để thay thế cho phương trình thứ hai trong hệ và giữ nguyên phương trình thứ nhất, ta được hệ phương trình mới tương đương với hệ phương trình đã cho.
Dạng 2: Giải hệ phương trình bằng phương pháp cộng đại số
Phương pháp giải: Để giải phương trình bằng phương pháp cộng đại số ta sử dụng quy tắc cộng đại số gồm hai bước sau:
Bước 1: Cộng hay trừ hai vế của hai phương trình của hệ phương trình đã cho để được hệ phương trình mới.
Bước 2: Dùng phương trình mới đấy thay thế cho một trong hai phương trình của hệ và giữ nguyên một phương trình kia ta được một hệ phương trình mới tương đương với hệ phương trình đã cho.
Bước 3: Giải hệ phương trình mới.
Dạng 3: Giải hệ phương trình bằng phương pháp đặt ẩn phụ
Phương pháp giải: Ta thực hiện theo ba bước sau
Bước 1: Lấy điều kiện của biến (nếu có)
Bước 2: Chọn ẩn phụ cho các biểu thức của hệ phương trình đã cho để được hệ phương trình bậc nhất hai ẩn dạng cơ bản.
Bước 3: Giải hệ phương trình bậc nhất vừa tìm được bằng các phương pháp thế hoặc cộng đại số.
Dạng 4: Hệ phương trình đẳng cấp
Phương pháp giải:
Để giải hệ phương trình đẳng cấp ta thực hiện theo ba bước sau:
Bước 1: Nhân phương trình (1) với a2 và phương trình (2) với a1 rồi trừ phương trình để làm mất hệ số tự do.
Bước 2: Phương trình chỉ còn hai ẩn x và y ta xét hai trường hợp.
Trường hợp 1: Nếu x = 0 hoặc y = 0. Ta thay vào phương trình ban đầu của hệ để giải ẩn còn lại.
Trường hợp 2: Nếu khác 0 hoặc y khác 0 ta chia cả hai vế phương trình cho bậc cao nhất của x hoặc y.
Bước 3: Giải phương trình với ẩn x/y hoặc y/x sau đó tìm nghiệm của hệ phương trình.
Dạng 5: Hệ phương trình đối xứng
Phương pháp giải: Hệ phương trình đối xứng là khi ta thay x bởi y và y bởi x thì hệ phương trình đã cho không đổi.
Để giải hệ phương trình này ta làm theo ba bước.
Bước 1: Đặt điều kiện (nếu có)
Bước 2: Đặt S = x + y; P = xy với điều kiện của S và P là
Bước 3: Thay x; y bởi S và P vào hệ phương trình. Tìm S, P rồi tìm x; y.
3. Hệ phương trình bậc nhất hai ẩn:
Hệ phương trình 2 ẩn là một hệ thống gồm hai phương trình bậc nhất có hai ẩn x và y, với cùng một điều kiện hoặc ràng buộc. Mục tiêu của việc giải hệ phương trình này là tìm ra giá trị của x và y thỏa mãn cả hai phương trình đồng thời.
Để giải hệ phương trình 2 ẩn, chúng ta có thể sử dụng các phương pháp như phương pháp cộng đại số, phương pháp thế hoặc phương pháp sử dụng ma trận.
Phương pháp cộng đại số thường được sử dụng để giải hệ phương trình 2 ẩn. Bước đầu tiên là viết hệ phương trình dưới dạng tường minh nhất có thể. Sau đó, ta có thể áp dụng các phép toán như cộng, trừ và nhân để loại bỏ ẩn số trong các phương trình và tìm ra giá trị của những ẩn số còn lại.
Ví dụ, để giải hệ phương trình sau:
a*x + b*y = c
a’*x + b’*y = c’
Đầu tiên, ta có thể nhân cả hai phương trình để loại bỏ ẩn số y bằng cách nhân a’ vào phương trình thứ nhất và nhân a vào phương trình thứ hai. Sau đó, ta có thể trừ phương trình thứ hai cho phương trình thứ nhất để loại bỏ ẩn số x.
Sau quá trình loại bỏ ẩn số, ta sẽ thu được giá trị của ẩn số còn lại. Từ đó, ta có thể thay vào một trong hai phương trình ban đầu để tính giá trị của ẩn số còn lại.
Đó là cách giải hệ phương trình 2 ẩn bằng phương pháp cộng đại số. Tuy nhiên, còn rất nhiều phương pháp khác để giải quyết hệ phương trình này, tùy thuộc vào đặc tình huống cụ thể.
THAM KHẢO THÊM:
