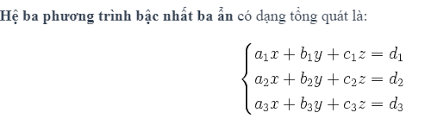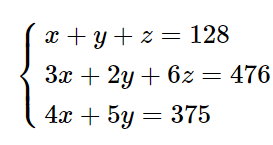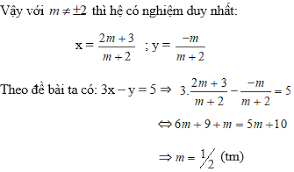Bài viết dưới đây gồm các bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết. Mời các bạn đón xem:
Mục lục bài viết
1. Bài tập chuyên đề Giải hệ phương trình lớp 9 có đáp án:
Câu 1: Giải hệ phương trình sau
Lời giải:
Cộng từng vế của hai phương trình trong hệ (I) ta được: 4x = 4
Do đó ta có hệ:
Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (1; -1).
Câu 2: Giải hệ phương trình sau:
Lời giải:
Nhân cả hai vế của phương trình thứ nhất với 2, khi đó ta được hệ tương đương:
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x; y) = (2; 1).
Câu 3: Cho hàm số y = ax + b. Xác định a, b để đồ thị hàm số đi qua hai điểm M(-1; 2) và N(√3;-7).
Hướng dẫn giải
Do hàm số y = ax + b có đồ thị đi qua M(-1; 2) nên thay x = -1 và y = 2 vào phương trình ta có: 2 = -a + b (1)
Tương tự, hàm số y = ax + b đi qua N(√3;-7) nên ta có: -7 = √3a + b (2)Chuyên đề Toán lớp 9
Câu 4: Trong mặt phẳng Oxy, viết phương trình đường thẳng AB trong các trường hợp:
a) A(-1; 1) và B(2; 4)
b) A(0; -1) và B(1; 0)
Hướng dẫn giải
Gọi phương trình đường thẳng cần tìm là y=ax+b
Vì đường thẳng đi qua A(-1; 1) nên ta có: 1=-a+b (1)
Vì đường thẳng đi qua B(2;4) nên ta có: 4=2a+b (2)
Từ (1) và (2) => a = 3 và b = 4
Vậ
b, Gọi phương trình đường thẳng cần tìm là y = ax + bVì đường thẳng đi qua A(0;-1) nên ta có: -1 = 0.a + b ⇔ b = -1.
Vì đường thẳng đi qua B(1;0) nên ta có: 0 = a + b (1)
Thay b = -1 vào (1) ta được a = 1
Vậy đường thẳng cần tìm là y = x – 1.
2. Dạng tổng quát của hệ phương trình bậc nhất hai ẩn:
Hệ hai phương trình bậc nhất hai ẩn có dạng tổng quát là: 
(I)
Trong đó x. y là hai ẩn, các chữ số còn lại là hệ số.
Nếu cặp số (x0;y0) đồng thời là nghiệm của cả hai phương trình của hệ thì (x0;y0) được gọi là nghiệm của hệ phương trình (I)
Giải hệ phương trình (I) ta tìm được tập nghiệm của nó.
3. Giải hệ phương trình bằng phương pháp cộng đại số:
Biến đổi hệ phương trình đã cho thành hệ phương trình tương đương
Cách giải hệ phương trình bằng phương pháp cộng đại số
Bước 1: Chọn ẩn muốn khử, thường là x (hoặc y)
Bước 2: Xét xem hệ số của ẩn muốn khử.
– Khi các hệ số của cùng một ẩn đối nhau thì ra cộng vế theo vế của hệ.
– Khi các hệ số của cùng một ẩn số bằng nhau thì ta trừ vế theo vế của hệ.
– Nếu các hệ số đó không bằng nhau thì ta nhân cả hai vế của phương trình với số thích hợp (nếu cần) sao cho các hệ số của x (hoặc y) trong hai phương trình của hệ là bằng nhau hoặc đối nhau (đồng nhất hệ số).
Bước 3: Cộng hoặc trừ từng vế hai phương trình của hệ đã cho để được một phương trình mới (phương trình một ẩn)
Bước 4: Dùng phương trình một ẩn thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia)
Bước 5: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Hướng dẫn giải
Nhân cả hai vế của phương trình x + 4y = 6 với 2 ta được 2x + 8y = 12
Hệ phương trình trở thành 
Lấy hai vế phương trình thứ hai trừ hai vế phương trình thứ nhất ta được
2x + 8y – (2x – 3y) = 12 – 1
=>2x + 8y – 2x + 3y = 11
=>11y = 11
=> y = 1
Thay y = 1 vào phương trình x + 4y = 6 ta được
x + 4 = 6
=> x = 6 – 4
=> x = 2
Vậy hệ phương trình có nghiệm (x; y) = (2; 1)
* Ta có thể trình bày như sau:
Vậy hệ phương trình có nghiệm (x; y) = (2; 1)
. Tính tổng S = m2 + n2Hướng dẫn giải
Ta có:
Nghiệm của phương trình là (x; y) = (m; n) = (2; 1)
S = m2 + n2 = 22 + 12 = 5
Vậy S = 5
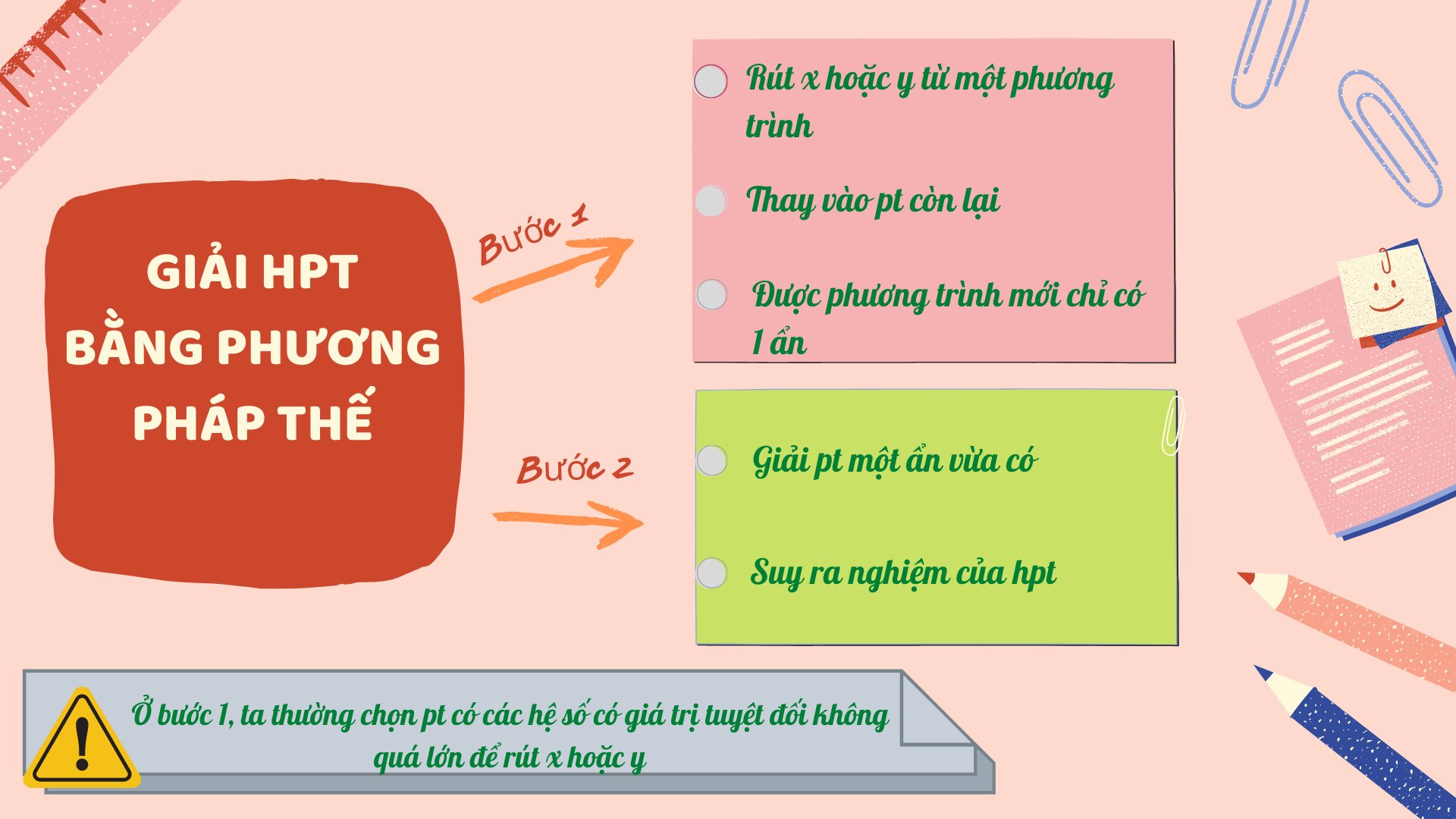
4. Giải hệ phương trình bằng phương pháp thế:
Biến đổi hệ phương trình đã cho thành hệ phương trình tương đương
Cách giải hệ phương trình bằng phương pháp thế
Bước 1: Từ một phương trình của hệ đã cho, ta biểu diễn một ẩn theo ẩn kia.
Bước 2: Thế ẩn đã biến đổi vào phương trình còn lại để được phương trình mới (Phương trình bậc nhất một ẩn)
Bước 3: Giải phương trình một ẩn vừa tìm được.
Bước 4: Thay giá trị vừa tìm được của ẩn vào biểu thức tìm được trong bước thứ nhất để tìm giá trị của ẩn còn lại.
Hướng dẫn giải
Hệ phương trình 
Rút x từ phương trinh trình thứ nhất ta được x = 3 – y
Thay x = 3 – y vào phương trình thứ hai ta được:
(3 – y)y – 2(3 – y) = -2
=> 3y – y2 – 6 + 2y = -2
=> y2 – 5y + 4 = 0
Do 1 – 5 + 4 = 0 => y = 1 hoặc y = 4
+) Với y = 4 => x = 3 – 4 = -1
+) Với y = 1 => x = 3 – 1 = 2
Vậy hệ phương trình có nghiệm (x; y) = (-1; 4) = (2; 1)
* Ta có thể trình bày bài như sau:
Vậy hệ phương trình có nghiệm (x; y) = (-1; 4) = (2; 1)
a) Giải hệ phương trình với m = 2 b) Tìm m để hệ phương trình có nghiệm duy nhất (x; y) trong đó x, y trái dấu. c) Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x = |y|Hướng dẫn giải
a) Với m = 2 thay vào hệ phương trình ta có:
b) Từ phương trình (1) ta có: x = 2y + 5
Thay x = 2y + 5 vào phương trình (2) ta được:
m(2y + 5) – y = 4
<=> 2my + 5m – y =4
<=> (2m – 1).y = 4- 5m (3)
<=> 
Hệ có nghiệm duy nhất khi và chỉ khi (3) có nghiệm duy nhất
=> 2m – 1 ≠ 0 => m ≠ 1/2
Ta có: 
Để x, y trái dấu <=> xy < 0
<=> 
<=> 4 – 5m < 0 <=> m > 4/5
Vậy m > 4/5 thì hệ phương trình có nghiệm duy nhất (x; y) trong đó x, y trái dấu.
c) Ta có: 
(4)
từ (4) suy ra 2m – 1 > 0 => m > 1/2
Với điều kiện m > 1/2 ta có:
(4) => |4 – 5m | = 3
=> 
Vậy m = 7/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x = |y|
a) Không giải hệ phương trình trên, cho biết với giá trị nào của m thì hệ phương trình có nghiệm duy nhất? b) Giải và biện luận hệ phương trình trên theo m.Hướng dẫn giải
a) Cách 1: Từ phương trình (2) ta có: y = 3m – 1 – 3x
Thay vào phương trình (1) ta được:
x + m(3m – 1 – mx) = m + 1
=> (m2 – 1)x = 3m2 – 2m – 1 (3)
Hệ phương trình có nghiệm duy nhất khi và chỉ khi phương trình (3) có nghiệm duy nhất tức là
m2 – 1 ≠ 0 => m ≠ ± 1
Cách 2: Hệ phương trình có nghiệm duy nhất khi và chỉ khi 
<=> 
b) Từ phương trình (2) ta có: y = 3m – 1 – mx.
Thay vào phương trình (1) ta được:
x + m(3m – 1 – mx) = m + 1
<=> x + 3m2 – m – m2x = m + 1
<=> (m2 – 1)x = 3m2 – 2m – 1 (3)
Trường hợp 1: m ≠ ± 1 khi đó hệ có nghiệm duy nhất
Trường hợp 2: m = 1 khi đó phương trình (3) trở thành: 0.x = 0
Vậy hệ có vô số nghiệm với mọi x thuộc R
Trường hợp 3: Với m = -1 khi đó phương trình (3) trở thành: 0.x = 4
=> Hệ phương trình vô nghiệm
5. Giải hệ phương trình bằng phương pháp đặt ẩn phụ:
Hướng dẫn giải
Điều kiện xác định của phương trình: 
Đặt 
Hệ phương trình trở thành: 
Cách 1: Giải hệ phương trình bằng phương pháp thế:
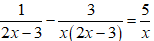
Cách 2: Giải hệ phương trình bằng phương pháp cộng đại số:
