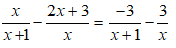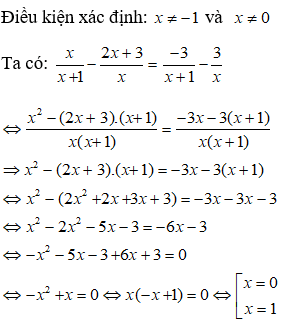Giá trị tuyệt đối là một trong những nội dung mới được học trong chương trình Toán 7 và là một nội dung quan trọng mà học sinh cần nắm chắc. Cùng tham khảo bài viết này lý thuyết và giá trị tuyệt đối và những bài tập vận dụng nhé:
Mục lục bài viết
1. Lý thuyết giá trị tuyệt đối:
* Định nghĩa: Khoảng cách từ điểm a đến điểm 0 trên trục số là giá trị tuyệt đối của một số a (a là số thực)
* Giá trị tuyệt đối của số không âm là chính nó, giá trị tuyệt đối của số âm là số đối của nó.
Tổng quát: Nếu a ≥ 0 → |a| = a
Nếu a < 0 → |a| = -a
Nếu x – a ≥ 0 → |x – a| = x – a
Nếu x – a ≤ 0 → |x – a| = a – x
* Tính chất
– Giá trị tuyệt đối của mọi số đều không âm
Tổng quát: |a| ≥ 0 với mọi a ∈ R. Cụ thể:
|a| =0 <=> a = 0
|a| ≠ 0 <=> a ≠ 0
– Hai số bằng nhau hoặc đối nhau thì có giá trị tuyệt đối bằng nhau và ngược lại hai số có giá trị tuyệt đối bằng nhau thì chúng là hai số bằng nhau hoặc đối nhau.
Tổng quát: |a| = |b| ↔ a = b hoặc a = -b
– Mọi số đều lớn hơn hoặc bằng đối của giá trị tuyệt đối của nó và đồng thời nhỏ hơn hoặc bằng giá trị tuyệt đối của nó.
Tổng quát: -|a| ≤ a ≤ |a| và -|a| = a ↔ a ≤ 0; a = |a| ↔ a ≥ 0
– Trong hai số âm số nào nhỏ hơn thì có giá trị tuyệt đối lớn hơn
Tổng quát: Nếu a < b < 0 → |a| > |b|
– Trong hai số dương số nào nhỏ hơn thì có giá trị tuyệt đối nhỏ hơn
Tổng quát: Nếu 0 < a < b → |a| < |b|
– Giá trị tuyệt đối của một tích bằng tích các giá trị tuyệt đối.
Tổng quát: |a.b| = |a|.|b|
– Giá trị tuyệt đối của một thương bằng thương hai giá trị tuyệt đối.
Tổng quát: |a/b| = |a|/|b|
– Bình phương của giá trị tuyệt đối của một số bằng bình phương số đó.
Tổng quát: |a|2 = a2
– Tổng hai giá trị tuyệt đối của hai số luôn lớn hơn hoặc bằng giá trị tuyệt đối của hai số, dấu bằng xảy ra khi và chỉ khi hai số cùng dấu.
Tổng quát: |a| + |b| ≥ |a + b| và |a| + |b| = |a + b| ↔ ab ≥ 0
2. Các dạng toán về giá trị tuyệt đối lớp 7:
1. Dạng 1: |A(x)| = k (Trong đó A(x) là biểu thức chứa x, k là một số cho trước)
* Cách giải:
– Nếu k < 0 thì không có giá trị nào của x thoả mãn đẳng thức (Vì giá trị tuyệt đối của mọi số đều không âm)
– Nếu k = 0 thì ta có |A(x)| = 0 → A(x) = 0
– Nếu k > 0 thì ta có: |A(x)| = k → A(x) = k hoặc A(x) = -k
Bài tập ví dụ: Tìm x, biết:
| a) |2x – 5| = 4 | b) 1/3 – |5/4 – 2x| = 1/4 | c) 1/2 – |x + 1/5| = 1/3 | d) 3/4 – |2x + 1| = 7/8 |
2. Dạng 2: 
(Trong đó A(x) và B(x) là hai biểu thức chứa x)
* Cách giải:
Vận dụng tính chất: 
ta có: 
Bài tập ví dụ: Tìm x biết:
3. Dạng 3: 
(Trong đó A(x) và B(x) là hai biểu thức chứa x)
* Cách 1: Ta thấy nếu B(x) < 0 thì không có giá trị nào của x thoả mãn vì giá trị tuyệt đối của mọi số đều không âm. Do vậy ta giải như sau:
(1)
Điều kiện: 
(*)
(1) Trở thành 
Đối chiếu giá tri x tìm được với điều kiện (*)
* Cách 2: Chia khoảng xét điều kiện bỏ dấu giá trị tuyệt đối:
Nếu 
Nếu 
Ta giải như sau:
· Nếu A(x) thì (1) trở thành: A(x) = B(x) (Đối chiếu giá trị x tìm được với điều kiện)
· Nếu A (x ) < 0 thì (1) trở thành: – A(x) = B(x) (Đối chiếu giá trị x tìm được với điều kiện)
Bài tập ví dụ: : Tìm x, biết:
4. Dạng 4: Đẳng thức chứa nhiều dấu giá trị tuyệt đối:
* Cách giải: Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối:
Căn cứ bảng trên xét từng khoảng giải bài toán (Đối chiếu điều kiện tương ứng)
Bài tập ví dụ: : Tìm x, biết:
3. Bài tập vận dụng giá trị tuyệt đối lớp 7:
Câu 1: Giá trị tuyệt đối của -3 là:
| A. – 2 | B. 2 | C. – 3 | D. 3 |
Đáp án: D
Câu 3: Có bao nhiêu số 
| A. 0 số | B. 1 số | C. 2 số | D. 3 số |
Đáp án: B
Đáp án: C
Đáp án: C
Câu 6: Biểu thức A = | 4x | + 2x – 1 với x < 0, rút gọn được kết quả là?
A. A = 6x – 1
B. A = 1 – 2x
C. A = – 1 – 2x
D. A = 1 – 6x
Câu 7: Tập nghiệm của phương trình: | 3x + 1 | = 5
A. S = {- 2} B. S = {4/3} C. S = {- 2;4/3} D. S = {Ø}
Đáp án: C
Câu 8: Tập nghiệm của phương trình | 2 – 3x | = | 2 – 5x | là?
A. S = {- 3;1} B. S = {- 3;7/5} C. S = {0;7/5} D. S = { – 3;1 }
Đáp án: B
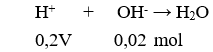
Câu 9: Giá trị m để phương trình | 3 + x | = m có nghiệm x = – 1 là?
A. m = 2 B. m = – 2 C. m = 1 D. m = – 1
Câu 10: Giá trị của m để phương trình | x – m | = 2 có nghiệm là x = 1?
A. m ∈ {1} B. m ∈ {- 1;3} C. m ∈ {- 1;0} D. m ∈ {1;2}
Đáp án: B
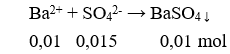Vậy giá trị m cần tìm là m ∈ { – 1;3 }Câu 11: Tính: 
Đáp án:
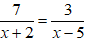
Câu 12: Tính giá trị của biểu thức:
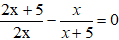
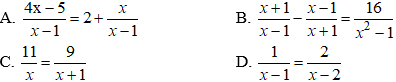
Câu 13: Tìm x, biết:
Đáp án:
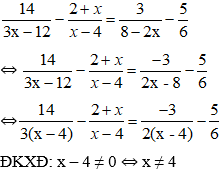
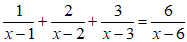
Câu 14: Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau:
a) A = 3x + 2 + | 5x | với x > 0.
b) A = | 4x | – 2x + 12 với x < 0.
c) A = | x – 4 | – x + 1 với x < 4
Hướng dẫn:
a) Với x > 0 ⇒ | 5x | = 5x
Khi đó ta có: A = 3x + 2 + | 5x | = 3x + 2 + 5x = 8x + 2
Vậy A = 8x + 2.
b) Ta có: x < 0 ⇒ | 4x | = – 4x
Khi đó ta có: A = | 4x | – 2x + 12 = – 4x – 2x + 12 = 12 – 6x
Vậy A = 12 – 6x.
c) Ta có: x < 4 ⇒ | x – 4 | = 4 – x
Khi đó ta có: A = | x – 4 | – x + 1 = 4 – x – x + 1 = 5 – 2x.
Vậy A = 5 – 2x
Câu 15: Giải các phương trình sau:
a) | 2x | = x – 6
b) | – 5x | – 16 = 3x
c) | 4x | = 2x + 12
d) | x + 3 | = 3x – 1
Hướng dẫn:
a) Ta có: | 2x | = x – 6
+ Với x ≥ 0, phương trình tương đương: 2x = x – 6 ⇔ x = – 6.
Không thỏa mãn điều kiện x ≥ 0.
+ Với x < 0, phương trình tương đương: – 2x = x – 6 ⇔ – 3x = – 6 ⇔ x = 2.
Không thỏa mãn điều kiện x < 0.
Vậ
b) Ta có: | – 5x | – 16 = 3x
+ Với x ≥ 0, phương trình tương đương: 5x – 16 = 3x ⇔ 2x = 16 ⇔ x = 8
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: – 5x – 16 = 3x ⇔ 8x = – 16 ⇔ x = – 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { – 2;8 }
c) Ta có: | 4x | = 2x + 12
+ Với x ≥ 0, phương trình tương đương: 4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: – 4x = 2x + 12 ⇔ – 6x = 12 ⇔ x = – 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = {- 2;6}
d) Ta có: | x + 3 | = 3x – 1
+ Với x ≥ – 3, phương trình tương đương: x + 3 = 3x + 1 ⇔ – 2x = – 2 ⇔ x = 1.
Thỏa mãn điều kiện x ≥ – 3
+ Với x < – 3, phương trình tương đương: – x – 3 = 3x + 1 ⇔ – 4x = 4 ⇔ x = – 1
Không thỏa mã điều kiện x < – 3
Vậy phương trình đã cho có tập nghiệm là S = {1}
4. Một số bài tập nâng cao giá trị tuyệt đối lớp 7:
Bài 1: Rút gọn biểu thức 
khi:
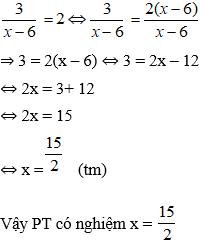
Hướng dẫn giải:
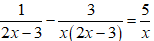
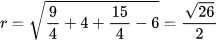
Hướng dẫn giải:
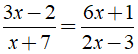
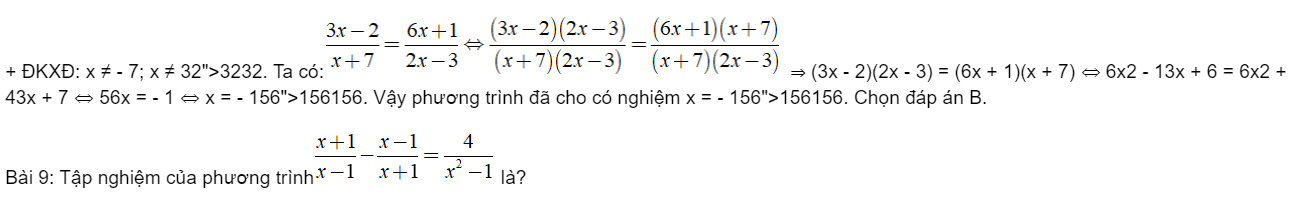
Bài 3: Tìm x, biết:
