Hướng dẫn cách giải hệ phương trình 2 ẩn bậc hai lớp 9

Giải hệ phương trình bậc 2 lớp 9 là một quy trình giải toán học thú vị và hữu ích cho học sinh. Bằng cách áp dụng phương pháp thế, học sinh có thể giải phương trình một ẩn và suy ra nghiệm của hệ phương trình đã cho. Việc giải các bài toán này không chỉ giúp học sinh rèn luyện kỹ năng giải toán mà còn phát triển tư duy logic và khả năng lập luận.

Mục lục bài viết

1 1. Cách giải hệ phương trình 2 ẩn bậc hai lớp 9 (cực hay):
2 2. Bài tập kèm lời giải:
3 3. Hệ phương trình bậc 2 là gì?
4 4. Phương trình bậc hai với hai ẩn số có dạng như thế nào?

1. Cách giải hệ phương trình 2 ẩn bậc hai lớp 9 (cực hay):

Phương pháp giải

Để giải hệ phương trình chứa 2 ẩn x và y gồm một phương trình bậc nhất và một phương trình bậc hai ta rút x hoặc y từ phương trình bậc nhất thế vào phương trình bậc hai

Ví dụ 1: giải hệ phương trình:

Giải

Từ phương trình (1) ⇒ y = 2x – 7(*). Thế vào phương trình (2) ta được:

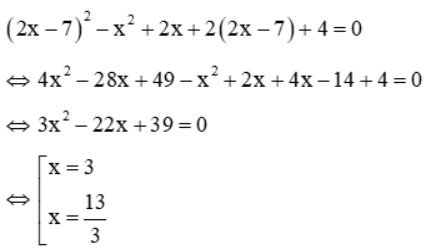
Ví dụ 2: Giải hệ phương trình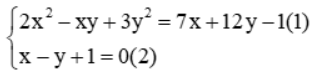

Giải

Từ phương trình (2) ⇒ y = x + 1(*). Thế vào phương trình (1) ta được

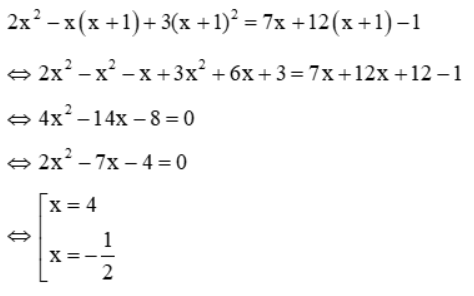
Ví dụ 3: Cho hệ phương trình

a. Giải hệ với m = 3

b. Tìm m để hệ có nghiệm duy nhất

Giải

Từ phương trình (1) ⇒ y = x + 1. Thế vào phương trình (2) ta được:

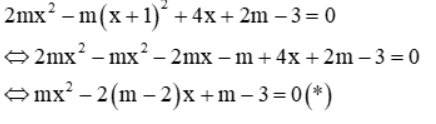
a. Với m = 3 thì phương trình (*) trở thành: 3x² – 2x = 0

b. Hệ có nghiệm duy nhất khi (*) có nghiệm duy nhất

TH1: Nếu m = 0 thì phương trình (*): 4x – 3 = 0 (thỏa mãn)

TH2: Nếu m ≠ 0 thì (*) là phương trình bậc 2 . Khi đó (*) có nghiệm duy nhất khi

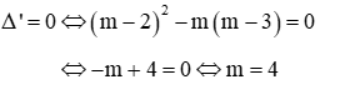
Vậy với m = 0 hoặc m = 4 thì hệ có nghiệm duy nhất

2. Bài tập kèm lời giải:

Câu 1: Cho hệ phương trình 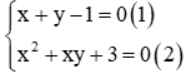. Rút y từ phương trình (1) thế vào phương trình (2) ta được phương trình nào sau đây

A. x + 3 = 0

B. 2x² + x + 3 = 0

C. -x + 3 = 0

D. –x² + x + 3 = 0

Giải

Từ (1)⇒ y = 1 – x. Thế vào (2):

2t² – 3t – 5 = 0

⇔ x² + x – x² + 3 = 0 ⇔ x + 3 = 0

Vậy đáp án đúng là A

Câu 2: Cho hệ phương trình . Biết rằng hệ đã cho có 2 nghiệm (x₁; y₁) và (x₂; y₂), tính x₁ + x₂

Giải

Từ (1) ⇒ y = x – 5. Thế vào (2): 2(x + x – 5)² – 3(x + x – 5) – 5 = 0

⇔ 2(2x – 5)² – 3(2x – 5) – 5 = 0

Đặt t = 2x – 5. Phương trình trở thành: 2t² – 3t – 5 = 0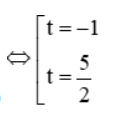

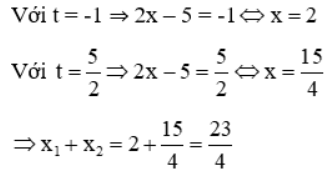
Vậy đáp án đúng là C

Câu 3: Cho hệ phương trình 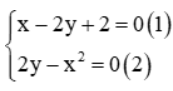. Biết rằng hệ đã cho có 2 nghiệm (x₁; y₁) và (x₂; y₂) trong đó x₁ > x₂ , tính x₁ + y₁

A. 1

B. 2

C. 3

D. 4

Giải

Vậy đáp án đúng là D

Câu 4: Cho hệ phương trình 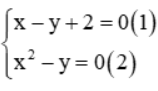. Rút x từ phương trình (1) thế vào phương trình (2) ta được phương trình nào sau đây

A. y² + 4 = 0

B. 3y² + y – 3 = 0

C.-y² – 4 = 0

D. y² – 5y + 4 = 0

Giải

Từ (1) x = y – 2. Thế vào (2): (y – 2)² – y = 0

⇔ y² – 4y + 4 – y = 0 ⇔ y² – 5y + 4 = 0

Vậy đáp án đúng là D

Câu 5: Cho hệ phương trình . Giá trị của m để hệ vô nghiệm là:

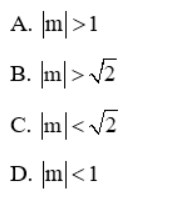
Giải

Biến đổi hệ đã cho về dạng:

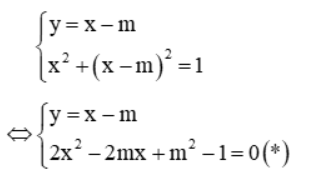
Hệ vô nghiệm khi phương trình (*) vô nghiệm

Vậy đáp án đúng là B

Câu 6: Cho hệ phương trình . Giá trị của m để hệ có nghiệm duy nhất là:

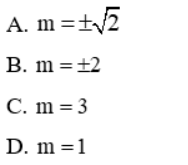
Giải

Biến đổi hệ đã cho về dạng:

Hệ có nghiệm duy nhất khi phương trình (*) có nghiệm duy nhất

Vậy đáp án đúng là A

Câu 7: Cho hệ phương trình 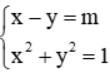. Giá trị của m để hệ có hai nghiệm là:

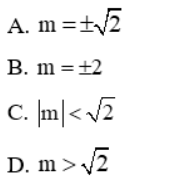
Giải

Biến đổi hệ đã cho về dạng:

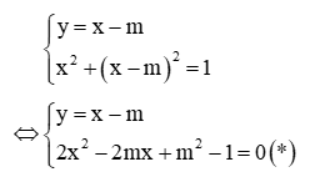
Hệ có 2 nghiệm khi phương trình (*) có 2 nghiệm

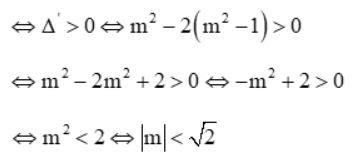
Vậy đáp án đúng là C

Câu 8: Cho hệ phương trình . Tìm m để hệ có hai nghiệm (x₁ ; y₁) và (x₂ ; y₂) sao cho là:

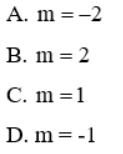
Giải

Biến đổi hệ đã cho về dạng:

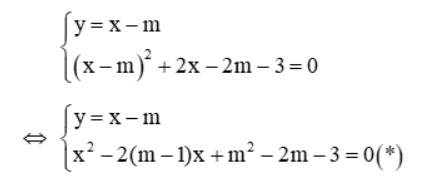
Hệ có 2 nghiệm khi phương trình (*) có 2 nghiệm

⇔ Δ’ > 0 ⇔ (m – 1)² – m² + 2m + 3 > 0 ⇔ 4 > 0 (∀ m)

⇒ phương trình (*) luôn có 2 nghiệm : x₁ = m + 1; x₂ = m – 3

Với x₁ = m + 1 ⇒ y₁ = 1

Với x₂ = m – 3 ⇒ y₂ = -3

Vậy đáp án đúng là B

Câu 9: Cho hệ phương trình 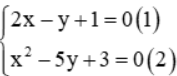. Rút y từ phương trình (1) thế vào phương trình (2) ta được phương trình nào sau đây

A. 2x² + 4x – 3 = 0

B. x² – 10x – 2 = 0

C. 3x² – 4x + 4 = 0

D. x² – 5x + 1 = 0

Giải

Vậy đáp án đúng là B

Câu 10: Số nghiệm của hệ phương trình 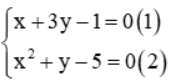là

A. 1

B. 2

C. 3

D. 4

Giải

Từ (1)⇒ x = 1 – 3y. Thế vào (2): (1 – 3y)² + y – 5 = 0

⇔ 9y² – 6y + 1 + y – 5 = 0 ⇔ 9y² – 5y – 4 = 0

Phương trình 9y² – 5y – 4 = 0 có a + b + c = 9 – 5 – 4 = 0 nên có 2 nghiệm y = 1, y =

Vậy đáp án đúng là B

Câu 11: Không giải hệ phương trình, dự đoán số nghiệm của hệ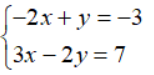

A. 0

B. Vô số

C. 1

D. 2

Lời giải:

Tập nghiệm phương trình -2x + y = -3 được biểu diễn bởi đường thẳng -2x + y = -3

Tập nghiệm phương trình 3x – 2y = 7 được biểu diễn bởi đường thẳng 3x – 2y = 7

Ta có ⇒ phương trình có một nghiệm duy nhất

Chọn đáp án C

Câu 12: Không cần vẽ hình, cho biết mỗi hệ phương trình sau có bao nhiêu nghiệm?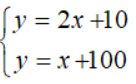

A. 1

B. Vô số

C. 0

D. 2

Lời giải:

+ Tập nghiệm của phương trình y = 2x + 10 được biểu diễn bởi đường thẳng d₁:y = 2x + 10.

+ Tập nghiệm của phương trình y = x + 100 được biểu diễn bởi đường thẳng d₂: y = x + 100.

Lại có: hệ số góc của hai đường thẳng d₁; d₂ khác nhau (2 ≠ 1) nên hai đường thẳng này cắt nhau.

Suy ra, hệ phương trình đã cho có nghiệm duy nhất.

Chọn đáp án A.

Câu 13: Không vẽ hình, hỏi hệ phương trình sau có bao nhiêu nghiệm:

A. Vô số nghiệm

B. 0

C.1

D. 2

Lời giải:

Ta có: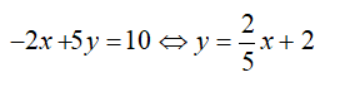

Nên tập nghiệm của phương trình – 2x + 5y = 10 được biểu diễn bởi đường thẳng (d1):

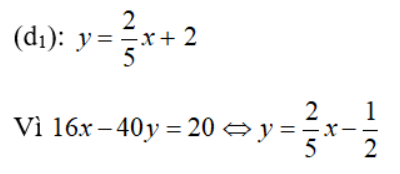
Nên tập nghiệm của phương trình 16x – 40y = 20 được biểu diễn bởi đường thẳng (d2):

Hai đường thẳng d₁; d₂ có cùng hệ số góc và có tung độ góc khác nhau nên d₁// d₂.

Suy ra, hệ phương trình đã cho vô nghiệm.

Chọn đáp án B.

Câu 14: Cho hệ phương trình . Tìm m để hệ phương trình đã cho vô nghiệm

A. m = 3

B. m = 1

C. m = -2

D. m = -1

Lời giải:

Nghiệm phương trình y = 2x + 20 được biểu diễn bởi đường thẳng (d₁): y =2x +20.

Nghiệm phương trình y = (2m – 4)x + 10 được biểu diễn bởi đường thẳng (d₂): y = (2m – 4)x + 10.

Để hệ phương trình đã cho vô nghiệm khi 2 đường thẳng d₁ // d₂

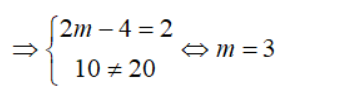
Chọn đáp án A.

3. Hệ phương trình bậc 2 là gì?

Hệ phương trình bậc 2 là một hệ gồm nhiều phương trình bậc 2 tương tự nhau, trong đó mỗi phương trình có dạng ax^2 + bx + c = 0, với a, b, và c là các hệ số, và x là biến số.

Để giải hệ phương trình bậc 2, chúng ta có thể sử dụng các phương pháp như:

1. Phương pháp suy diễn: Đầu tiên, ta giải phương trình bậc 2 một ẩn thông thường bằng cách sử dụng các công thức giải phương trình bậc 2. Tiếp theo, ta dùng kết quả này để suy ra giá trị của biến số trong các phương trình khác.

2. Phương pháp thế: Ta chọn một phương trình trong hệ và giải biến số đó theo biến số còn lại. Sau đó, ta thế giá trị của biến số đã tìm được vào phương trình còn lại để tìm giá trị của biến số thứ hai.
Lưu ý rằng để thu được kết quả chính xác, ta cần kiểm tra lại nghiệm tìm được bằng cách thực hiện kiểm tra nghiệm.

4. Phương trình bậc hai với hai ẩn số có dạng như thế nào?

Phương trình bậc hai với hai ẩn số có dạng như sau:

ax^2 + bx + c = 0

Trong đó, a, b và c là các hệ số, và x là biến số.

Để giải phương trình này, ta có thể sử dụng công thức nghiệm của phương trình bậc hai, được gọi là công thức nghiệm của Vi-et.

Công thức nghiệm của Vi-et cho phương trình bậc hai có dạng như sau:

x = (-b ± √(b^2 – 4ac)) / 2a

Trong đó, ± đại diện cho hai nghiệm của phương trình, và √ là ký hiệu căn bậc hai.

Quá trình giải phương trình bậc hai có thể được thực hiện theo các bước sau:

Tìm các hệ số a, b và c của phương trình.

2. Tính giá trị của biểu thức b^2 – 4ac (gọi là delta hay Δ).

3. Kiểm tra giá trị của delta để xác định số nghiệm của phương trình:

– Nếu delta > 0, phương trình có hai nghiệm phân biệt.

– Nếu delta = 0, phương trình có nghiệm kép.

– Nếu delta < 0, phương trình không có nghiệm thực.

4. Tính giá trị của hai nghiệm x bằng cách sử dụng công thức nghiệm của Vi-et.

Đó là cách giải phương trình bậc hai với hai ẩn số.

THAM KHẢO THÊM:

1. Cách giải hệ phương trình 2 ẩn bậc hai lớp 9 (cực hay):

2. Bài tập kèm lời giải:

3. Hệ phương trình bậc 2 là gì?

4. Phương trình bậc hai với hai ẩn số có dạng như thế nào?

Tìm kiếm