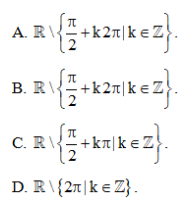Tập xác định của hàm số là kiến thức về môn Đại số lớp 10 mà tất cả các em học sinh cần phải nắm chắc. Dưới đây là bài viết về chủ đề: Tập xác định của hàm số y = 1/(sinx-cosx) là gì? bao gồm phần trả lời cho câu hỏi cùng những bài tập mở rộng, mời bạn đọc theo dõi.
Mục lục bài viết
1. Tập xác định của hàm số y = 1/(sinx-cosx) là gì?
Lời giải:
Đáp án đúng là: C
Biểu thức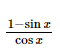 
có nghĩa khi cos x ≠ 0 hay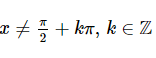 
Vậy tập xác định của hàm số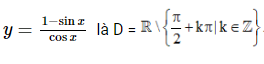 
2. Bài tập về tìm tập xác định của hàm số trong Sách Bài Tập Toán lớp 11:
Bài 31 trang 21 SBT Toán 11 Tập 1: Tập xác định của hàm số
Y = √ (1+cos2x) là
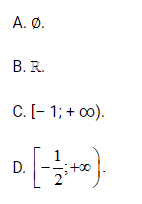
Đáp án đúng là: B
Biểu thức √(1+cos2x) có nghĩa khi 1 + cos 2x ≥ 0.
Mà cos 2x ∈ [– 1; 1] nên 1 + cos 2x ≥ 0 với mọi x ∈ ℝ.
Do đó, hàm số y=√(1+cos2x) xác định với mọi x ∈ ℝ.
Bài 32 trang 21 SBT Toán 11 Tập 1: Tập xác định của hàm số
Y = √ [(1−cosx)/(1+sinx)] là
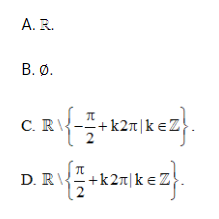
Lời giải:
Đáp án đúng là: C
Biểu thức √ [(1−cosx)/(1+sinx)] có nghĩa khi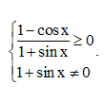 
Do cos x ∈ [– 1; 1] nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.
Và sin x ∈ [– 1; 1] nên 1 + sin x ≥ 0 với mọi x ∈ ℝ.
Do đó để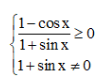 
thì 1 + sin x ≠ 0 hay sin x ≠ – 1, khi đó x≠(−π/2)+k2π,k∈Z
Vậy tập xác định của hàm số y= √ [(1−cosx)/(1+sinx)] là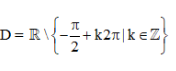 
Bài 33 trang 22 SBT Toán 11 Tập 1: Tập xác định của hàm số
y= (1−sinx)/cosx là
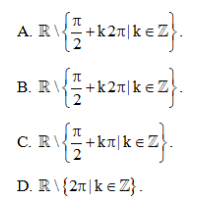
Lời giải:
Đáp án đúng là: C
Biểu thức (1−sinx)/cosx có nghĩa khi cos x ≠ 0 hay x≠π/2+kπ,k∈Z
Vậy tập xác định của hàm số y= (1−sinx)/cosx là D =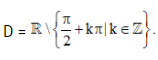 
Bài 34 trang 22 SBT Toán 11 Tập 1: Tập xác định của hàm số
y=tanx+1/ (1+cotx^2) là
Lời giải:
Đáp án đúng là: A
Hàm số y=tanx+1/ (1+cotx^2) xác định khi tan x và cot x xác định (do 1 + cot2 x > 0 với mọi x khi cot x xác định).
Mà tan x xác định khi x≠π/2+kπ, k∈Z , cot x xác định khi x ≠ kπ, k ∈ ℤ.
Do đó hàm số y=tanx+1/ (1+cotx^2) xác định khi x≠kπ2, k∈Z.
Vậy tập xác định của hàm y=tanx+1/ (1+cotx^2) là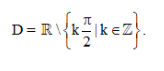 
Bài 35 trang 22 SBT Toán 11 Tập 1: Hàm số nào sau đây là hàm số lẻ?
A. y = – 2cos x.
B. y = – 2sin x.
C. y = tan x – cos x.
D. y = – 2 sin x + 2.
Lời giải:
Đáp án đúng là: B
Xét hàm số y = – 2sin x, ta có:
+ Tập xác định: D = ℝ.
+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = – 2sin(– x) = – 2 . (– sin x) = 2 sin x = – f(x).
Do đó, hàm số y = – 2sin x là hàm số lẻ.
Bài 36 trang 22 SBT Toán 11 Tập 1: Hàm số nào sau đây là hàm số chẵn?
A. y = cos x + 5.
B. y = tan x + cot x.
C. y = sin(– x).
D. y = sin x – cos x.
Lời giải:
Đáp án đúng là: A
Xét hàm số y = cos x + 5, ta có:
+ Tập xác định: D = ℝ.
+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = cos(– x) + 5 = cos x + 5 = f(x).
Do đó, hàm số y = cos x + 5 là hàm số chẵn.
Bài 37 trang 22 SBT Toán 11 Tập 1: Hàm số y = cos x nghịch biến trên khoảng:
A. (0; π).
B. (π; 2π).
C. (−π/2;π/2)
D. (– π; 0).
Lời giải:
Đáp án đúng là: A
Hàm số y = cos x nghịch biến trên mỗi khoảng (k2π; π + k2π).
Do đó hàm số y = cos x nghịch biến trên khoảng (0; π).
Bài 38 trang 22 SBT Toán 11 Tập 1: Hàm số nào trong các hàm số sau đồng biến trên khoảng
(π/2;3π/2) ?
A. y = sin x.
B. y = cos x.
C. y = tan x.
D. y = cot x.
Lời giải:
Đáp án đúng là: C
Ta có: (π/2;3π/2) = (−π/2+π; π/2+π)
Do hàm số y = tan x đồng biến trên khoảng (−π/2;π/2) nên hàm số đó cũng đồng biến trên khoảng (π/2;3π/2)
Bài 39 trang 22 SBT Toán 11 Tập 1: Hàm số y = sin x đồng biến trên khoảng
A. (9π/2;11π/2).
B. (11π/2;13π/2).
C. (10π; 11π).
D. (9π; 10π).
Lời giải:
Đáp án đúng là: B
Ta có: (11π/2;13π/2) = (−π/2+6π; π/2+6π).
Do hàm số y = sin x đồng biến trên khoảng (−π/2; π/2) nên hàm số đó cũng đồng biến trên khoảng (11π/2;13π/2).
Bài 40 trang 22 SBT Toán 11 Tập 1: Số giá trị α ∈ [− π; 2π] sao cho
cosα=1/3 là:
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải:
Đáp án đúng là: C
Xét đồ thị hàm số y = cos x trên [− π; 2π] và đường thẳng y = 1/3.
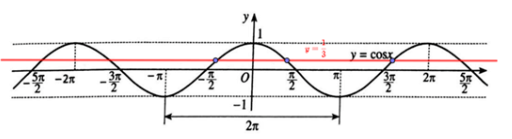
Ta thấy đường thẳng y = 1313 cắt đồ thị hàm số y = cos x trên [− π; 2π] tại 3 điểm.
Khi đó có 3 giá trị của x ∈ [− π; 2π] để cosx=1/3 hay có 3 giá trị của α ∈ [− π; 2π] để cosα=1/3 .
Bài 41 trang 22 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số:
a) y=√(1+sin3x)
Bài 42 trang 23 SBT Toán 11 Tập 1: Xét tính chẵn, lẻ của các hàm số:
a) y=√(1+sin3x) ;
b) y=sin2x/√(1−cosx) ;
c) y=√(1+cos2x)/sinx .
d) y=1/ (sinx+cosx) ;
e) y=1/(1+sinxcosx) ;
g) y=√(cosx−1) .
Lời giải:
a) Vì sin 3x ∈ [− 1; 1] nên 1 + sin 3x ≥ 0 với mọi x ∈ ℝ.
Do đó biểu thức √(1+sin3x) có nghĩa với mọi x ∈ ℝ.
Vậy tập xác định của hàm số y=√(1+sin3x) là D = ℝ.
b) Vì cos x ∈ [− 1; 1] nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.
Nên biểu thức sin2x/√(1−cosx) có nghĩa khi 1 – cos x ≠ 0 hay cos x ≠ 1, tức là x ≠ k2π, k ∈ ℤ.
Vậy tập xác định của hàm số y= sin2x/√(1−cosx) là D=R \ {k2π | k∈ ℤ
c) Biểu thức √(1+cos2x)/sinx có nghĩa khi ….
Mà cos 2x ∈ [− 1; 1] nên 1 + cos 2x ≥ 0 với mọi x ∈ ℝ.
Và sin x ≠ 0 khi x≠kπ,k∈Z.
Vậy tập xác định của hàm số y= =√(1+cos2x)/sinx là D =R\ { kπ |k∈Z}
d) Biểu thức 1/ (sinx+cosx) có nghĩa khi sin x + cos x ≠ 0
⇔ sin x ≠ – cos x ⇔ tan x ≠ – 1.
Mà tan x ≠ – 1 khi x≠−π/4+kπ,k∈Z.
Vậy tập xác định của hàm số y=1/ (sinx+cosx) là D=R \ {−π/4+kπ|k∈Z}
e) Ta có: 1 + sin x cos x = 1+sin2x/2.
Vì – 1 ≤ sin 2x ≤ 1 nên 1/2≤(1+sin2x/2)≤3/2 với mọi x ∈ ℝ.
Do đó 1 + sin x cos x > 0 với mọi x ∈ ℝ.
Khi đó biểu thức 1/(1+sinxcosx) có nghĩa với mọi x ∈ ℝ.
Vậy tập xác định của hàm số y=1/(1+sinxcosx) là D = ℝ.
g) Biểu thức √(cosx−1) có nghĩa khi cos x – 1 ≥ 0 hay cos x ≥ 1.
Mà cos x ∈ [− 1; 1] với mọi x ∈ ℝ.
Do đó, biểu thức =√(cosx−1) có nghĩa khi cos x = 1, tức là x = k2π, k ∈ ℤ.
Vậy tập xác định của hàm số y =√(cosx−1) là D = {k2π| k ∈ ℤ}.
3. Bài tập mở rộng kèm lời giải:
Bài 1: Tìm tập xác định D của hàm số
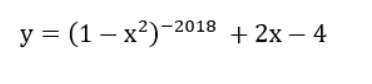
Lời giải:
Hàm số xác định khi và chỉ khi 1-x2 ≠ 0 ⇔ x ≠ ±1
Bài 2: Tìm tập xác định D của hàm số
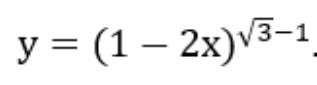
Lời giải: Hàm số xác định khi và chỉ khi 1-2x > 0 ⇔ x < 1/2
Bài 3: Tìm tập xác định D của hàm số
y = (2x – 4) -2018
Lời giải: Hàm số xác định khi và chỉ khi 2x-4 ≠ 0 ⇔ x ≠ 2
Bài 4: Tìm tập xác định D của hàm số
y = (4 – x) 3/11
Lời giải: Hàm số xác định khi và chỉ khi 4-x > 0 ⇔ x < 4
Bài 5: Tìm tập xác định D của hàm số
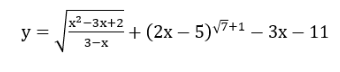
Lời giải: Hàm số xác định khi và chỉ khi 1+x-2×2 > 0 ⇔ -1/2 < x < 1
