Tập xác định của hàm số y = tan(2x-pi/3) là gì?

1. Tập xác định của hàm số y = tan(2x-pi/3) là:

A. x khác pi/6 + kpi/2

B. x khác 5pi/12 + kpi

C. x khác pi/2 + kpi

D. => x khác 5pi/6 + kpi/2 ( k thuộc Z )

Điều kiện xác định: cos ( 2x – pi/3 ) khác 0

=> 2x – pi/3 khác pi/2 + kpi

=> x khác 5pi/6 + kpi/2 ( k thuộc Z )

Chọn D

2. Lý thuyết về tập xác định hàm số lượng giác:

a. Hàm số y = sinx

– Tập xác định: D = R

– Tập giá trị: [-1;1]

b. Hàm số y = cosx

– Tập xác định: D = R 

– Tập giá trị: [-1;1]

c. Hàm số y = tanx  

– Tập xác định: D = R \ { pi/2 + kπ, k ∈ Z}  

– Tập giá trị:R  

d. Hàm số y = cotx

– Tập xác định: D = R \ { kπ, k ∈ Z} 

– Tập giá trị: R  

3. Các dạng bài tập kèm lời giải:

Dạng 1. Tìm tập xác định của hàm số lượng giác

– Phương pháp giải:

y= f(x)/g(x)  xác định khi g(x) ≠ 0  

y=căn f(x)  xác định khi f(x) ≥ 0

y= f(x)/căn g(x)  xác định khi g(x) > 0

y = tan[u(x)] xác định khi u(x) ≠ pi/2 + kπ, k ∈ Z

y = cot[u(x)] xác định khi u(x) ≠ kπ, k ∈ Z

sin x ≠ 0 khi x ≠ kπ (k ∈ Z)   

cos x ≠ 0 khi x ≠ pi/2 + kπ (k ∈ Z)  

– Ví dụ minh họa: 

Ví dụ 1. Tìm tập xác định của hàm số sau

a) y= tan ( 3x + pi/3 )

b) y= căn ( 2-sin x )

Lời giải

a)   y= tan ( 3x + pi/3 ) = sin ( 3x + pi/3 ) / cos ( 3x + pi/3 )

Vậy tập xác định của hàm số là  

b) Điều kiện xác định: 2 – sin x ≥ 0  

⇔ sin x ≤ 2 (đúng ∀x ∈ R ) vì -1 ≤ sin x ≤ 1 ∀x ∈ R 

Vậy tập xác định của hàm số là D = R.

Ví dụ 2. Tìm tập xác định của hàm số sau 

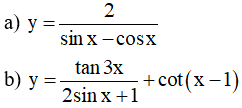
Lời giải

a) Điều kiện xác định: sin x – cos x ≠ 0 ⇔ sin x ≠ cos x (*)

+ Trường hợp 1: cosx = 0. Ta có sin²x + cos²x = 1 ⇔ sin² x = 1 ⇔ sin x = ±1.

Hiển nhiên sin x ≠ cos x

+ Trường hợp 2: cos x ≠ 0. Chia cả hai vế cho cosx

Vậy tập xác định của hàm số là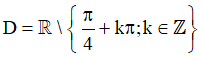  

b) 

Điều kiện xác định: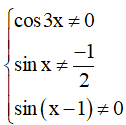  

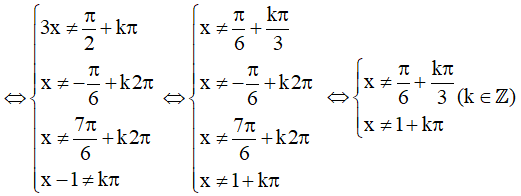
Dạng 2. Tìm tập giá trị của hàm số lượng giác

– Phương pháp giải:

Sử dụng tính bị chặn của hàm số lượng giác

– Ví dụ minh họa:

Ví dụ 1. Tìm tập giá trị của các hàm số sau:

a) y = 2sin3x – 5

b) y = 2sin (x2 -pi/12 )+5

c) y = |cos(3x-2)| + 4

Lời giải

a) Ta có:  

-1 ≤ sin 3x ≤ 1 ∀x ∈ R

⇔ -2 ≤ 2sin 3x ≤ 2 ∀x ∈ R 

⇔ -7 ≤ 2sin 3x – 5 ≤ -3 ∀x ∈ R

Vậy tập giá trị: T = [-7;-3].

b) Ta có: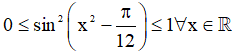  

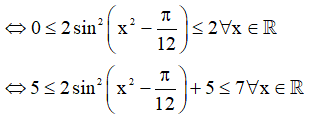
Vậy tập giá trị: T = [5;7].

c) Ta có: 0 ≤ |cos(3x – 2)| ≤ 1∀x ∈ R 

⇔ 4 ≤ |cos(3x – 2)| + 4 ≤ 5∀x ∈ R 

Vậy tập giá trị: T = [4;5].  

Ví dụ 2. Tìm tập giác trị của các hàm số sau:  

a)  

b) y = cos2x + 4sinx +1

Lời giải

a) Điều kiện xác định: sinx +1 ≥ 0 ⇔ sinx ≥ -1∀x ∈ R.

Tập xác định D = R.

Ta có: -1 ≤ sin x ≤ 1 ∀x ∈ R

⇔ 0 ≤ sinx + 1 ≤ 2 ∀x ∈ R  

Vậy tập giá trị: T = [-2,√2 – 2 ]

b) y = cos2x + 4sinx +1 = 1 – 2sin²x + 4sinx +1 = -2sin²x + 4sinx + 2 = -2(sinx – 1)² + 4.

Ta có: -1 ≤ sin x ≤ 1 ∀x ∈ R   

⇔ -2 ≤ sin x – 1 ≤ 0 ∀x ∈ R  

⇔ 0 ≤ (sin x – 1)² ≤ 4 ∀x ∈ R  

 ⇔ -8 ≤ -2(sin x – 1)² ≤ 0 ∀x ∈ R 

⇔ -4 ≤ -2(sin x – 1)² + 4 ≤ 4 ∀x ∈ R  .

Vậy tập giá trị: T = [-4;4].

Dạng 3. Tìm m để hàm số lượng giác có tập xác định là R

– Phương pháp giải:

m ≥ f(x) ∀x ∈ [a,b] => m ≥

m > f(x) ∀x ∈ [a,b] => m >

m ≤ f(x) ∀x ∈ [a,b] => m ≤

m < f(x) ∀x ∈ [a,b] => m <  

– Ví dụ minh họa:

Ví dụ 1. Tìm m để hàm số y= căn ( sin x + m ) xác định trên R.

Lời giải

Để hàm số xác định trên R thì sin x + m ≥ 0 ∀x ∈ R ⇔ -sin x∀x ∈ R .

Mà ta có -1 ≤ sin x ≤ 1 ∀x ∈ R ⇔ -1 ≤ -sin x ≤ 1 ∀x ∈ R 

Nên m ≥ 1

Ví dụ 2. Tìm m để hàm số  xác định trên R.

Lời giải

Ta có:  

Hàm số xác định trên R khi (sinx – 1)² + m – 1 ≥ 0 ∀x ∈ R ⇔ m  ≥ 1 – (sinx – 1)² ∀x ∈ R

Ta có:  

-1 ≤ sin x ≤ 1 ∀x ∈ R  

⇔ -2 ≤ sin x – 1 ≤ 0 ∀x ∈ R 

⇔ 0 ≤ (sinx – 1)² ≤ 4 ∀x ∈ R

⇔ -4 ≤ -(sinx – 1)² ≤ 0 ∀x ∈ R 

⇔ -3 ≤ 1 – (sinx – 1)² ≤ 1 ∀x ∈ R

Vậy m ≥ 1 

4. Câu hỏi trắc nghiệm kèm đáp án:

Câu 1. Tập xác định của hàm số y= cot ( 2x-pi/3 ) là

Câu 2. Tập xác định của hàm số y = tan x + cot x là

Câu 3. Tập xác định của hàm số y= căn ( sin x +1 ) là:

A. D = [ -1,+∞)                                          B. D = R

C. D = R \ ( pi/2 + kpi, k thuộc Z )                            D. D = (-∞, -1]

Câu 4. Tập xác định của hàm số 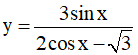 là:

Câu 5. Tập xác định của hàm số 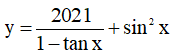 là

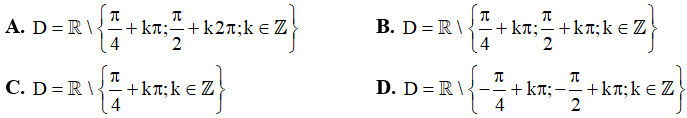
Câu 6. Tập giá trị của hàm số y = 1 – 2|sin2x| là

A. [1;3]                      B. [-1;1]                     C. [-1;3]                    D. [-1;0]

Câu 7. Tập giá trị của hàm số  là

A. [2;3]                      B. [1;2]                      C. [2;4]                      D. [3;4]

Câu 11. Tập giá trị của hàm số y = 2 + sinxcosx có dạng T = [m,M]. Giá trị của m là: 

Câu 12. Tập giá trị của hàm số y = 2sin3x +1 là

A. [-1;1]                    B. [-5;7]                     C. [0;2]                      D. [-1;3]

Câu 13. Tìm m để hàm số 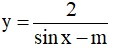 xác định trên R.

A. m ∈ (-∞; -1) ∪ (1, +∞)                            B. m ∈ (-∞; -1] ∪ [1, +∞)  

C. m ≠ 1                                                     D. m ∈ [-1;1] 

Câu 14. Hàm số 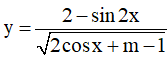 có tập xác định R khi và chỉ khi:

A. m > 3                    B. m < -1                   C. m ≥ 3                     D. m ≤ -1

Câu 15. Tìm tất cả các giá trị của tham số m để hàm số  có tập xác định là R.

A. m>=-3/2             B. m>=5/2               C. Không có m thỏa mãn          D. m ≥ 5 

Bài 16. Tìm tập giá trị của hàm số y = sinx + cosx.

Bài 17. Tìm tập giá trị của hàm số: y = sin x. cos x

Bài 18. Tìm tập giá trị của hàm số: y = 1-sin x

Bài 19. Tìm tập giá trị của hàm số: y = sin (2x-5 )

Bài 20. Tìm tập giá trị của hàm số: y = cos x – sin x

Đáp án