Công thức và cách tính tổng cấp số nhân lùi vô hạn chuẩn

1. Khái niệm cấp số nhân:

Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn) trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q

Dãy dố (U_n) được xác định bởi: thì dãy số này được gọi là cấp số nhân, q là công bội.

Có thể hiểu cấp số nhân có dạng: a, aq, aq², aq³, aq⁴, …… với a là số hạn đầu tiên và q là công bội

Ví dụ: Cấp số có số hạng đầu bằng 2 và công sai bằng 2 là 2, 4, 8, 16, 32, 64, 128, …..

2. Số hạng tổng quát và tổng một cấp số nhân:

Cấp số nhân bắt đầu là phần tử u₁ và công bội thì số hạng thứ n của cấp số cộng được tính theo công thức:

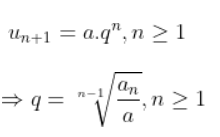
Tổng số hạng đầu của cấp số nhân: 

Nhân cả 2 vế với: ( 1 – q)

Vì tất cả cá số hạng khác đã loại trừ lẫn nhau: 

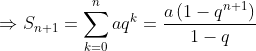
3. Cấp số nhân lùi vô hạn, công thức tính tổng các cấp số nhân lùi vô hạn và ví dụ:

(U_n) có công bội q, |q| < 1 được gọi là cấp số nhân lùi vô hạn

Ví dụ: 1/2, 1/4, 1/8, 1/16, …. là một cấp số nhân lùi vô hạn với công bội q = 1/2

Tổng của tất cả các số hạng trong một cấp số nhân lùi vô hạn là một giá trị hữu hạn và hoàn toàn có thể tính được.

Giả sử ta có cấp số nhân lùi vô hạn U_n

Khi đó tổng của các số hạng thuộc U_n là: 

S_n = u₁ + u₂ + u₃ + ….. + u_n-1 + u_n

Giới hạn hai vế ta sẽ được: 

Đây cũng chính là công thức tính tổng các cấp số nhân lùi vô hạn

Ví dụ 1: Tính tổng của cấp số nhân lùi vô hạn U_n với

Giải: 

Ta có: u1=1/3; q=1/3

Áp dụng công thức tính tổng cấp số nhân lùi vô hạn: 

s=1/2

Ví dụ 2: Cho cấp số nhân lùi vô hạn có số hạng đầu là 4, công bội là  1/2 . Hãy tính tổng tất cả các số hạng thuộc cấp số nhân đó.

Giải:

Áp dụng công thức ta tính được tổng tất cả các số hạng của cấp số nhân đó là:  s=8

4. Bài tập vận dụng:

Bài 1: Cho hình vuông ABCD có cạnh bằng a và có diện tích S₁ . Nối 4 trung điểm A₁, B₁, C₁, D₁ ta được hình vuông thứ 2 có diện tích S₂. Tiếp tục như thế, ta được hình vuông A₁B₂C₂D₂ có diện tích S₃ …. Tiếp tục quá trình trên ta được hình vuông lần lượt có diện tích là  S₄, S₅, S₆, ….. , S₁₀₀. Tính tổng

Giải: 

Có Là cấp số nhân có công bội bằng 1/2

Do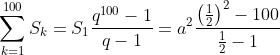

Bài 2: Chi cấp số nhân (un) có u3 = 24 và u4 = 48. Hãy tính tổng 5 số hạng đầu tiên của cấp số đó

Giải: 

Gọi q là công bội của cấp số nhân (un), ta có: q = 48/24 = 2

Do đó, theo định lý 2, ta được: 24 = u3 = u1.22

Suy ra u1 = 6. Vì thế, theo định lý 3, ta được S5 = 6. (1-25) / (1-2) = 186

Bài 3: Cho dãy số (U_n) với . Tính tổng của dãy U_n

Giải: 

Vì U_n là tổng n số hạng đầu tiên của một cấp số nhân có U₁ = 1/2 và q = (-1)/2

=> s=1/3

Bài 4: Cho cấp số nhân lùi vô hạn (V_n) với số hạng đầu V₁ = -1 và công bội q = x². Tìm tổng của cấp số nhân lùi vô hạn trên và bốn số hạng đầu: 

Giải: 

Ta áp dụng công thức

Từ đó bốn số hạng đầu của dãy là -1; -x²; -x⁴; -x⁶

Bài 5: Cho cấp số nhân lùi vô hạn (V_n) với số hạng đầu v₁ = 2 và công bội q = x^₃ . Tính tổng của cấp số nhân lùi vô hạn trên và bốn hạng đầu

Giải: 

Ta áp dụng công thức

Từ đó bốn số hạng đầu của dãy là 2; 2x³; 2x⁶; 2x⁹

Bài 6: Một cấp số nhân lùi vô hạn có tổng các số hạng bằng 56, tổng bình phương các số hạng bằng 448. Số hạng đầu tiên của cấp số nhân đó là? 

Giải: 

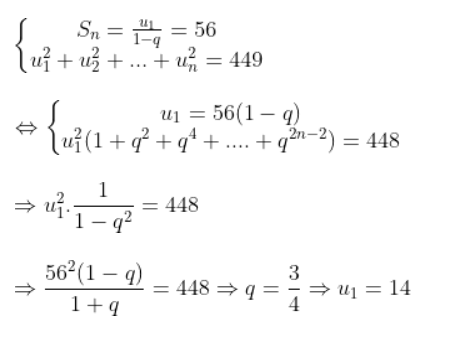
Bài 7: Tính tổng của cấp số nhân lùi vô hạn sau: 2; -1; 1/2; -1/4; 1/8; … ; ….

Giải: 

U_n chính là cấp số nhân có : U₁ = 2, q = -1/2

s=4/3

Bài 8: Câu nào sau đây là đáp án đúng

A. Cấp số nhân lùi vô hạn có U₁ = 15, S = 60 ⇒ q = 3/4

B. Cấp số nhân lùi vô hạn có công bội q thì tổng

C. Cấp số nhân lùi vô hạn có u₁ = -4, S = -169 ⇒ q = -5/4

D. u₁ = 3; q = -1/3 suy ra s=9/2

Đáp án cần chọn là A. Vì q = 3/4 < 1 ⇒ Đây là cấp sô nhân lùi vô hạn có suy ra s=60

Bài 9: Cấp số nhân lùi vô hạn có u₁ = -50, S = 100. Tìm 5 số hạng đầu của cấp số đó

A. 50; 25; 12,25; 6,125; 3,025

B. 50; 25; 12,5; 6,5; 3,25

C. 50; 25; 12,5; 6,5; 3,125 

D. 50; 25; 12,5; 6,25; 3,125

Chọn đáp án D

Bài 10: Cấp số nhân lùi vô hạn có u₁ = -1; q=x. Tìm 3 số hạng đầu của cấp số nhân lùi vô hạn đó 

A. 1; x; -x²

B. -1; x; x²

C. -1; x; x²

D. -1; -x; -x²

Đáp án cần chọn là D

Bài 11: Tính tổng của cấp số nhân lùi vô hạn sau:  

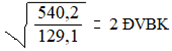
Giải: 

U_n chính là cấp số nhân có u₁ = 5,

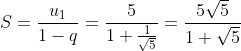
Đáp án cần chọn là: C

Bài 12: Tính tổng của cấp số nhân lùi vô hạn sau: -3; 0; 3; -0,03; 0,003; …

A. 11/30

B. 30/11

C. -11/30

D. -16/11

Giải: 

U_n chính là cấp số nhân có : u₁ = -3; q = 0,1

-> s= -16/11

Đáp án cần chọn là D

Bài 13: Tổng của một số nhân lùi  vô hạn có kết quả là 5/3  trong đó tổng 3 số hạng đầu bằng 39/25. Hãy tìm u₁ và q cấp số đó

A. u₁ = 1; q = -2/5

B. u₁ = -1; q = -2/5

C. u₁ = -1; q = 2/5

D. u₁ = 1; q= 2/5

Giải: 

s=5/3

u₁ + u₂ + u₃ = u₁(1 + q + q²) = 39/25

⇒ q = 2/5 ⇒ u₁ = 1

Đáp án cần chọn là: D

Bài 14: Tính tổng S = 16 + 4 + 1 + … +  + ….

A. S = 62/3

B. S = 64/5

C. S = 16/3

D. S = 64/3

Giải:

+ Bước 1: ta ta kiểm tra xem tổng trên có phải là cấp số nhân lùi vô hạn không? 

+ Bước 2: Áp dụng công thức phù hợp để tính tổng 

Ta có:

Mà |q| = |1/4| < 1 nên tổng trên là cấp số nhân lùi vô hạn

Ta có s=64/3

Chọn đáp án D

Bài 15: Cho cấp số nhân lùi vô hạn (v_n) có v₁ = 20, S = 100. Tìm 6 số hạng đầu tiên của dãy (v_n):

A. 20; 16; 12,8; 10,24; 8,192; 6,5536

B. 20; 16; 12,8; 10,25; 8,192; 6,5536

C. 20; 16,25; 12,8; 10,24; 8,192; 6,5536

D. 20; 16; 12,8; 10,24; 8,192; 6,5

Giải: 

Ta áp dụng công thức tính tổng số hạng lùi vô hạn: , với số hạng đầu v₁ = 20 và tổng S = 100 ⇒ công bội q. Từ đó ta viết được 6 số hạng đầu của cấp số trên

Áp dụng công thức tính tổng cấp số nhân lùi vô hạn

Từ đó suy ra 6 số hạng đầu tiên của dãy số (v_n): 20; 16; 12,8; 10, 24; 8,192; 6,5536

Chọn đáp án A

Bài 16: Cho số b = 3,13131313… ( chu kỳ 13) là số thập phân vô hạn tuần hoàn, số b dược biểu diễn dưới dạng phân số tối giản b = x/y, trong đó x, y là các số nguyên dương. Tìm tổng x + y

A. x + y = 211

B. x + y = 409

C. x + y = 130

D. x + y = 490

Giải: 

Cách 1: Ta có b = 3,13131313….= là tổng của cấp số nhân lùi vô hạn với số hạng đầu v₁ = 13/100 và công bội q = 1/100 nên ta áp dụng công thức tính cấp số nhân lùi vô hạn

⇒ x = 310; y = 99 

Vậy x + y = 310 + 99 = 409

Cách 2: Đặt d = 0,113131313… ⇒ 100d = 13 + d ⇔ d = 13/99

⇒ b = 3 + d = 3 + 13/99 = 310/99

⇒ x = 310; y = 99

Vậy x + y = 310 + 99 = 409

Cách 3: Sử dụng MTCT. Ta nhập số 3,1313131313 vào máy ( nhiều bộ số 13, cho tràn màn hình) rồi bấm =

Ta thu được kết quả trên máy tính 3,(13) = 310/99

⇒ x = 310; y = 99

Vậy x + y = 310 + 99 = 409

Chọn đáp án B