Tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện

1. Hướng dẫn giải bài toán tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện:

Để giải bài toán tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện cho trước, ta có thể làm theo các bước sau:

– Bước 1: Viết lại hệ phương trình dưới dạng ma trận đơn vị và ma trận hệ số.

– Bước 2: Tính định thức của ma trận hệ số và tìm điều kiện để định thức khác không.

– Bước 3: Giải hệ phương trình và tìm nghiệm của hệ phương trình theo m.

– Bước 4: Thay nghiệm của hệ phương trình vào điều kiện cho trước và tìm giá trị của m thỏa mãn điều kiện đó.

Ví dụ:

– Ta có hệ phương trình:

x + y = 1 (1)

mx + y = 2 (2)

Để hệ phương trình có nghiệm duy nhất, ta cần điều kiện:

D = |1 1| ≠ 0

   |m 1|

Từ đó, ta suy ra: m ≠ 1

Giả sử m ≠ 1, ta giải hệ phương trình bằng phương pháp Cramer:

x = D_x / D = |1 1| / D = (2 – m) / (1 – m)

      |2 1|

y = D_y / D = |1 2| / D = (m – 1) / (1 – m)

      |m 2|

Để nghiệm của hệ phương trình thỏa mãn điều kiện x > y, ta cần:

(2 – m) / (1 – m) > (m – 1) / (1 – m)

Điều này tương đương với:

(2 – m)(1 – m) > (m – 1)(1 – m)

Rút gọn, ta được:

-2m + 3 > 0

Hay:

m < 3/2

Vậy, để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện x > y, ta cần: m ≠ 1 và m < 3/2

2. Lý thuyết bài toán giải hệ phương trình:

Một hệ phương trình là một tập hợp các phương trình có chung các ẩn số. Mục tiêu của bài toán về giải hệ phương trình là tìm ra các giá trị của các ẩn số sao cho thỏa mãn tất cả các phương trình trong hệ. Có nhiều phương pháp để giải hệ phương trình, tùy thuộc vào loại và số lượng của các phương trình. Một số phương pháp thông dụng là:

– Phương pháp cộng trừ: Đây là phương pháp đơn giản nhất, dựa trên việc cộng hoặc trừ hai vế của hai phương trình để loại bỏ một ẩn số. Phương pháp này thường được áp dụng cho hệ hai phương trình bậc nhất hai ẩn.

– Phương pháp thế: phương pháp dựa trên việc biểu diễn một ẩn số qua các ẩn số khác, rồi thay vào một phương trình để giải, thường được áp dụng cho hệ hai phương trình bậc nhất hai ẩn.

– Phương pháp định thức: phương pháp dựa trên việc biểu diễn hệ phương trình dưới dạng ma trận, rồi sử dụng công thức Cramer để tính nghiệm. Phương pháp này có thể áp dụng cho hệ nhiều phương trình bậc nhất nhiều ẩn.

Ví dụ: Giải hệ phương trình sau bằng các phương pháp khác nhau:

x + y = 5

x – y = 1

– Phương pháp cộng trừ: Cộng hai vế của hai phương trình, ta được:

2x = 6

=> x = 3

Thay x = 3 vào một trong hai phương trình, ta được:

3 + y = 5

=> y = 2

Vậy nghiệm của hệ là (3, 2).

– Phương pháp thế: Từ phương trình thứ hai, ta có:

x = y + 1

Thay vào phương trình thứ nhất, ta được:

y + 1 + y = 5

=> 2y = 4

=> y = 2

Thay y = 2 vào một trong hai phương trình, ta được:

x + 2 = 5

=> x = 3

Vậy nghiệm của hệ là (3, 2).

– Phương pháp định thức: Biểu diễn hệ phương trình dưới dạng ma trận, ta được:

| x |   | y |   |   |

|—|—|—|—|—|

| 1 |   | 1 |   | 5 |

| 1 | – | 1 |   | 1 |

Sử dụng công thức Cramer, ta có:

x = D_x / D

y = D_y / D

Trong đó:

D = |1   1|

    |1  -1| = -2

D_x = |5   1|

      |1  -1| = -6

D_y = |1   5|

      |1   1| = -4

Vậy:

x = -6 / -2 = 3

y = -4 / -2 = 2

Vậy nghiệm của hệ là (3, 2).

3. Các bài tập cơ bản tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện:

– Bài 1: Tìm m để hệ phương trình sau có nghiệm duy nhất:

x + y = 2

mx + y = 3

Đáp án: m ≠

Giải thích: Để hệ phương trình có nghiệm duy nhất, ta cần điều kiện:

D = |1 m|

    |1 1| ≠ 0

Tức là m ≠ 1.

– Bài 2: Tìm m để hệ phương trình sau có nghiệm duy nhất:

x + y = 2

x + my = 3

Đáp án: m ≠ 1

Giải thích: Tương tự bài 1, ta cần điều kiện:

D = |1 1|

    |1 m| ≠ 0

Tức là m ≠ 1.

– Bài 3: Tìm m để hệ phương trình sau có nghiệm duy nhất:

x + y = m

x – y = 2

Đáp án: m ≠ 0

Giải thích: Để hệ phương trình có nghiệm duy nhất, ta cần điều kiện:

D = |1 1|

    |1 -1| ≠ 0

Tức là D = -2 ≠ 0. Điều này luôn đúng với mọi giá trị của m. Tuy nhiên, ta cần thêm điều kiện để hệ phương trình có nghiệm thực, đó là:

Dx = |m 1|

     |2 -1| ≠ 0

Tức là m ≠ 0.

– Bài 4: Tìm m để hệ phương trình sau có nghiệm duy nhất:

mx + y = 2

x + my = 3

Đáp án: m ≠ -1 và m ≠ 0

Giải thích: Để hệ phương trình có nghiệm duy nhất, ta cần điều kiện:

D = |m 1|

    |1 m| ≠ 0

Tức là m² + 1 ≠ 0. Điều này luôn đúng với mọi giá trị của m. Tuy nhiên, ta cần thêm điều kiện để hệ phương trình có nghiệm thực, đó là:

Dx = |2 1|

     |3 m| ≠ 0

Tức là m ≠ -3/2.

– Bài 5: Tìm m để hệ phương trình sau có nghiệm duy nhất:

mx + y = -2

x + my = -3

Đáp án: m > -2 và m < -1 hoặc m > -1 và m < -2/3

Giải thích: Để hệ phương trình có nghiệm duy nhất, ta cần điều kiện:

D = |m 1|

    |1 m| ≠ 0

Tức là m² + 1 ≠ 0. Điều này luôn đúng với mọi giá trị của m. Tuy nhiên, ta cần thêm điều kiện để hệ phương trình có nghiệm thực, đó là:

Dx = |-2 1|

     |-3 m| ≠ 0

Tức là -2m +3 ≠ 0. Giải bất phương trình này, ta được:

m > -2 và m < -1 hoặc m > -1 và m < -2/3.

4. Các bài tập nâng cao tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn điều kiện:

Bài 1: Tìm các giá trị m để hệ  có nghiệm.

• Phân tích. Để có kết quả nhanh hơn ta sẽ đặt ngay

Lời giải

Bài 2: Tìm các giá trị của m để hệ  (I) có nghiệm.

Lời giải.

• Vậy mọi nghiệm của hệ (II) đều là nghiệm của hệ (I)

5. Một số bài tập giải hệ phương trình:

Bài 1: Giải hệ phương trình

Phân tích. Phương trình (2) là bậc nhất đối với y nên ta dùng phép thế.

Lời giải.

TH 1 : x = 0 không thỏa mãn (2)

Chú ý.: Hệ phương trình này có thể thế theo phương pháp sau:

• Hệ

•  Phương pháp thế thường là công đoạn cuối cùng khi ta sử dụng các phương pháp khác

Bài 2: Giải hệ phương trình

Lời giải.

•  

• TH 2.. TH này vô nghiệm do ĐK.

Vậy hệ có nghiệm duy nhất (1; 1)

Bài 3: Giải hệ phương trình

• Phân tích. Các biểu thức trong ngoặc có dạng a + b và a – b nên ta chia hai vế pt thứ nhất cho căn 3x và chia hai vế pt thứ hai cho căn 7y

Lời giải.

Bài 4: Giải hệ phương trình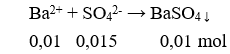

. 

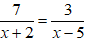Cộng vế 3 phương trình của hệ ta được :

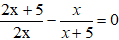
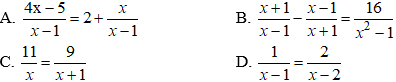
• Từ (4) và (1) ta có

• Tứ (4) và (2) ta cóy=3/4 Từ (4) và (3) ta có z=9/11

• Tương tự, từ (5), (1), (2), (3) ta có.x=-5/6, y=-1, z=-5/4

• Vậy hệ có tập nghiệm là

S =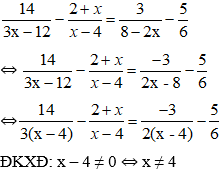

Bài 5: Giải hệ phương trình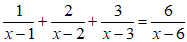

• Phân tích. Rõ ràng, việc giải phương trình (2) hay kết hợp (1) với (2) không thu được kết quả khả quan nên chúng ta tập trung để giải (1).

Lời giải

.

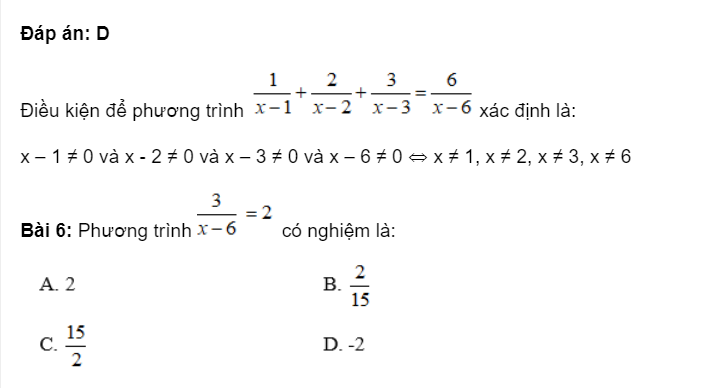
Chú ý. Do có thể phân tích được thành tích của hai nhân tử bậc nhất đối y (hay x) nên có thể giải pt (1) bằng cách coi (1) là pt bậc hai ẩn y (hoặc x).