Dưới đây là bài viết về chủ đề: Tổng hợp kiến thức và các dạng bài tập Toán 10 chi tiết từ những lý thuyết cơ bản về định nghĩa đến những tính chất cũng như các dạng bài tập cần lưu ý, mời bạn đọc theo dõi.
Mục lục bài viết
- 1 1. Kiến thức về Mệnh đề:
- 2 2. Kiến thức về Tập hợp:
- 3 3. Kiến thức về Hàm số:
- 4 4. Kiến thức về Đại cương về phương trình:
- 5 5. Kiến thức về Bất đẳng thức:
- 6 6. Kiến thức về Bảng phân bố tần số và tần suất:
- 7 7. Kiến thức về Cung và góc lượng giác:
- 8 8. Kiến thức về Véc tơ:
- 9 9. Kiến thức về Tích vô hướng của hai vectơ và ứng dụng:
- 10 10. Kiến thức về Phương pháp tọa độ trong mặt phẳng:
- 11 11. Các dạng bài tập Toán 10 chi tiết:
1. Kiến thức về Mệnh đề:
Mệnh đề
Mệnh đề là một tuyên bố có thể đúng hoặc sai, không tồn tại trạng thái chưa xác định nào giữa chúng.
Mệnh đề chứa biến:
Mệnh đề có thể chứa biến, là các ký tự có thể thay đổi giá trị. Ví dụ, mệnh đề là một mệnh đề chứa biến, với mỗi giá trị của , chúng ta có thể xác định mệnh đề là đúng hoặc sai.
Phủ định của mệnh để:
Phủ định của mệnh đề P kí hiệu là . Nếu mệnh đề P đúng thì
sai, P sai thì
đúng.
Ví dụ: : “3 là số nguyên tố”
: “3 không là số nguyên tố”
Mệnh đề kéo theo:
Mệnh đề “nếu P thì Q ” được gọi là mệnh đề kéo theo. Kí hiệu .
Mệnh đề chỉ sai khi P đúng và Q sai.

P: giả thiết (điều kiện đủ để có Q)
Q: kết luận (điều kiện cần để có P)


Ghi nhớ:

2. Kiến thức về Tập hợp:
Tập hợp và phần tử
Tập hợp (còn gọi là tập) là một khái niệm cơ bản của toán học, không định nghĩa.
Giả sử đã cho tập hợp A.
Để chỉ a là một phần tử của tập hợp A, ta viết a ∈ A (đọc là a thuộc A).
Để chỉ a không phải là một phần tử của tập hợp A, ta viết a ∈ A (đọc là P không thuộc A).
Cách xác định tập hợp
Một tập hợp có thể được xác định bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó.
Vậy ta có thể xác định một tập hợp bằng một trong hai cách sau
Liệt kê các phần tử của nó.
Chỉ ra tính chất đặc trưng cho các phần tử của nó.
Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.
Tập hợp rỗng
Tập hợp rỗng, kí hiệu là ø, là tập hợp không chứa phần tử nào.
Nếu A không phải là tập hợp rỗng thì A chứa ít nhất một phần tử.
A ≠ ø <=> ∃x : x ∈ A.
– Tập hợp con
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B và viết A B (đọc là A chứa trong B).
Thay cho A B ta cũng viết B ⊃ A (đọc là B chứa A hoặc B bao hàm A)
Như vậy A ⊂ B <=> (∀x : x ∈ A => x ∈ B).
Nếu A không phải là một tập con của B ta viết A ⊄ B.
Ta có các tính chất sau :
A Avới mọi tập hợp A
Nếu A ⊂ B và B ⊂ C thì A ⊂ C (h.4)
ø A với mọi tập hợp A.
– Tập hợp bằng nhau
Khi A ⊂ B và B ⊂ A ta nói tập hợp A bằng tập hợp B và viết là A = B. Như vậy
A = B <=> (∀x : x ∈ A <=> x ∈ B).
3. Kiến thức về Hàm số:
– Hàm số. Tập xác định của hàm số Giả sử có hai đại lượng biếnthiên x và y, trong đó x nhận giá trị thuộc tập số D. Nếu với mỗi giá trị của x thuộc tập D có một và chỉ một giá trị tương ứng của x thuộc tập số thực R thì ta có một hàm số. Ta gọi x là biến số và y là hàm số của x. Tập hợp D được gọi là tập xác định của hàm số. – Cách cho hàm số Một hàm số có thể được cho bằng các cách sau. Hàm số cho bằng bảng Hàm số cho bằng biểu đồ Hàm số cho bằng công thức Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa. – Đồ thị của hàm số Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x,f(x)) trên mặt phẳng tọa độ với x thuộc D. Sự biến thiên của hàm số – Ôn tập Hàm số y = f(x) gọi là đồng biến (tăng) trên khoảng (a ; b) nếu ∀x1, x2 ∈ (a ; b) : x1 < x2 => f(x1) < f(x2) Hàm số y = f(x) gọi là nghịch biến (giảm) trên khoảng (a ; b) nếu : ∀x1, x2 ∈ (a ; b) : x1 < x2 => f(x1) > f(x2) – Bảng biến thiên Xét chiều biến thiên của một hàm số là tìm các khoảng đồng biến và các khoảng nghịch biến của nó. Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên. Ví dụ. Dưới đây là bảng biến thiên của hàm số y = x2.  Hàm số y = x2 xác định trên khoảng (hoặc trong khoảng) ( –∞ ; +∞) và khi x dần tới +∞ hoặc dần tới –∞ thì y đều dần tới +∞. Tại x = 0 thì y = 0. Để diễn tả hàm số nghịch biến trên khoảng (–∞ ; 0) ta vẽ mũi tên đi xuống (từ +∞ đến 0). Để diễn tả hàm số đồng biến trên khoảng (0 ; +∞) ta vẽ mũi tên đi lên (từ 0 đến +∞).
Hàm số y = x2 xác định trên khoảng (hoặc trong khoảng) ( –∞ ; +∞) và khi x dần tới +∞ hoặc dần tới –∞ thì y đều dần tới +∞. Tại x = 0 thì y = 0. Để diễn tả hàm số nghịch biến trên khoảng (–∞ ; 0) ta vẽ mũi tên đi xuống (từ +∞ đến 0). Để diễn tả hàm số đồng biến trên khoảng (0 ; +∞) ta vẽ mũi tên đi lên (từ 0 đến +∞).
Ôn tập về hàm số bậc nhất
y = ax + b (a ≠ 0) Tập xác định D = R Chiều biến thiên Với a > 0 hàm số đồng biến trên Với a < 0 hàm số nghịch biến trên Bảng biến thiên

Đồ thị Đồ thị của hàm số là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn song song với đường thẳng y = ax (nếu b ≠ 0) (nếu b ≠ 0) và đi qua hai điểm A(0 ; b), B( -b/a ; 0)
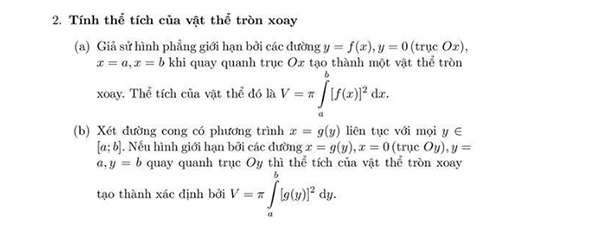
Hàm số hằng y = b Đồ thị hàm số y = b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung tại điểm (0 ; b). Đường thẳng này gọi là đường thẳng y = b.

Hàm số y = |x|
Hàm số y = |x| có liên quan chặt chẽ với hàm bậc nhất. – Tập xác định Hàm số y = |x| xác định với mọi giá trị của x ∈ R tức là tập xác định y = |x|. – Chiều biến thiên Theo định nghĩa của giá trị tuyệt đối, ta có y = |x| =  Từ đó suy ra hàm số y = |x| nghịch biến trên khoảng ( –∞ ; 0) và đồng biến trên khoảng (0 ; +∞). Bảng biến thiên Khi x > 0 và dần tới +∞ thì y = x dần tới +∞, khi x < 0 dần tới –∞ thì y = –x cũng dần tới +∞. Ta có bảng biến thiên sau
Từ đó suy ra hàm số y = |x| nghịch biến trên khoảng ( –∞ ; 0) và đồng biến trên khoảng (0 ; +∞). Bảng biến thiên Khi x > 0 và dần tới +∞ thì y = x dần tới +∞, khi x < 0 dần tới –∞ thì y = –x cũng dần tới +∞. Ta có bảng biến thiên sau

– Đồ thị Trong nửa khoảng [0; +∞) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = x. Trong khoảng (–∞; 0) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = –x

CHÚ Ý Hàm số y = |x| là một hàm số chẵn, đồ thị của nó nhận Oy làm trục đối xứng.
4. Kiến thức về Đại cương về phương trình:
Khái niệm phương trình
– Phương trình một ẩn
Phương trình ẩn x là mệnh đề chứa biến có dạng
F(x) = g(x) (1)
Trong đó f(x) và g(x) là những biểu thức của x. Ta gọi f(x) là vế trái, g(x) là vế phải của phương trình (1).
Nếu có số thực x0 sao cho f(xo) = g(xo) là mệnh đề đúng thì xo được gọi là một nghiệm của phương trình (1).
Giải phương trình (1) là tìm tất cả các nghiệm của nó (nghĩa là tìm tập nghiệm).
Nếu phương trình không có nghiệm nào cả thì ta nói phương trình vô nghiệm (hoặc nói tập nghiệm của nó là rỗng).
– Điều kiện của một phương trình
Khi giải phương trình (1), ta cần lưu ý với điều kiện đối với ẩn số x để f(x) và g(x) có nghĩa (tức là mọi phép toán đều thực hiện được). Ta cũng nói đó là điều kiện xác định của phương trình (hay gọi tắt là điều kiện của phương trình).
– Phương trình nhiều ẩn
Ngoài các phương trình một ẩn, ta còn gặp những phương trình có nhiều ẩn số, chẳng hạn
3x + 2y = x2 – 2xy + 8, (2)
4x2 – xy + 2z = 3z2 + 2xz + y2 ( 3)
Phương trình (2) là phương trình hai ẩn (x và y), còn (3) là phương trình ba ẩn (x, y và z).
Khi x = 2, y = 1 thì hai vế của phương trình (2) có giá trị bằng nhau, ta nói cặp (x; y) = (2; 1) là một nghiệm của phương trình (2).
Tương tự, bộ ba số (x; y; z) = (–1; 1; 2) là một nghiệm của phương trình (3).
– Phương trình chứa tham số
Trong một phương trình (một hoặc nhiều ẩn), ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem như những hằng số và được gọi là tham số.
Phương trình tương đương và phương trình hệ quả
– Phương trình tương đương
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
– Phép biến đổi tương đương
Định lí
Nếu thực hiện các phép biển đổi sau đây trên một phương trình mà không làm thay đổi điều kiện của nó thì ta được một phương trình mới tương đương
A) cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức;
B) nhân hoặc chia hai vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.
Chú ý: chuyển vế và đổi dấu một biểu thức thực chất là thực hiện phép cộng hay trừ hai vế với biểu thức đó.
– Phương trình hệ quả
Nếu mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình f1(x) = g1(x) thì phương trình f1(x) = g1(x) được gọi là phương trình hệ quả của phương trình f(x) = g(x)
Ta viết
F(x) = g(x) => f1(x) = g1(x).
Phương trình hệ quả có thể có thêm nghiệm không phải là nghiệm của phương trình ban đầu. Ta gọi đó là nghiệm ngoại lai.
Lý thuyết phương trình quy về phương trình bậc nhất, bậc hai
Ôn tập về phương trình bậc nhất, bậc hai
– Phương trình bậc nhất
Cách giải và biện luận phương trình dạng ax + b = 0 được tóm tắt trong bảng sau
Khi a ≠ 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn.
– Phương trình bậc hai
Cách giải và công thức nghiệm của phương trình bậc hai được tóm tắt trong bảng sau

– Định lí vi–ét
Nếu phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1, x2 thì
x1 + x2 = -b/a , x1x2 = c/a.
Ngược lại, nếu hai số u và v có tổng u + v = S và tích uv = P thì u và v là các nghiệm của phương trình
x2 – Sx + P = 0.
Phương trình quy về phương trình bậc nhất, bậc hai
Có nhiều phương trình khi giải có thể biến đổi về phương trình bậc nhất hoặc bậc hai.
Sau đây ta xét hai trong các dạng phương trình đó.
– Phương trình chứa ẩn trong dấu giá trị tuyệt đối
Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta có thể dùng định nghĩa của giá trị tuyệt đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.
Ví dụ 1. Giải phương trình |x – 3| = 2x + 1. (3)
Giải
Cách 1
A) nếu x ≥ 3 thì phương trình (3) trở thành x – 3 = 2x + 1. Từ đó x = –4.
Giá trị x = –4 không thỏa mãn điều kiện x ≥ 3 nên bị loại.
B) nếu x < 3 thì phương trình (3) trở thành –x + 3 = 2x + 1. Từ đó x = 2/3
Giá trị này thỏa mãn điều kiện x < 3 nên là nghiệm.
Kết luận. Vậy nghiệm của phương trình là x = 2/3
Cách 2. Bình phương hai vế của phương trình (3) ta đưa tới phương trình hệ quả
(3) => (x – 3)2 = (2x + 1)2
=> x2 – 6x + 9 = 4x2 + 4x + 1
=> 3x2 + 10x – 8 = 0.
Phương trình cuối có hai nghiệm là x = –4 và x = 2/3
Thử lại ta thấ
– Phương trình chứa ẩn dưới dấu căn
Để giải các phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một phương trình hệ quả không chứa ẩn dưới dấu căn.
Ví dụ 2. Giải phương trình
![]() = x – 2 (4).
= x – 2 (4).
Giải.
Điều kiện của phương trình (4) là x ≥ 3/2
Bình phương hai vế của phương trình (4) ta đưa tới phương trình hệ quả
(4) => 2x – 3 = x2 – 4x + 4
=> x2 – 6x + 7 = 0.
Phương trình cuối có hai nghiệm là x = 3 + √2 và x = 3 – √2 . Cả hai giá trị này đều thỏa mãn điều kiện của phương trình (4), nhưng khi thay vào phương trình (4) thì giá trị x = 3 – √2 bị loại (vế trái dương còn vế phải âm), còn giá trị x= 3 + √2 là nghiệm (hai vế cùng bằng √2 + 1).
Kết luận. Vậy nghiệm của phương trình (4) là x= 3 + √2 .
5. Kiến thức về Bất đẳng thức:
– Khái niệm bất đẳng thức
Các mệnh đề dạng “a > b” hoặc “a > b” được gọi là bất đẳng thức.
– Bất đẳng thức hệ quả và bất đẳng thức tương đương
Nếu mệnh đề “a > b => c > d” đúng thì ta nói bất đẳng thức c > d là bất đẳng thức hệ quả của bất đẳng thức a > b và cũng viết là a > b => c > d.
Nếu bất đẳng thức a > b là hệ quả của bất đẳng thức c > d và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là a > b <=> c > d.
– Tính chất của bất đẳng thức
Như vậy để chứng minh bất đẳng thức a > b ta chỉ cần chứng minh a – b > 0. Tổng quát hơn, khi so sánh hai số, hai biểu thức hoặc chứng minh một bất đẳng thức, ta có thể sử dụng các tính chất của bất đẳng thức được tóm tắt trong bảng sau
Chú ý
Ta còn gặp các mệnh đề dạng a ≤ b hoặc a ≥ b. Các mệnh đề dạng này cũng được gọi là bất đẳng thức. Để phân biệt, ta gọi chúng là các bất đẳng thức không ngặt và gọi các bất đẳng thức dạng a < b hoặc a > b là các bất đẳng thức ngặt. Các tính chất nêu trong bảng trên cũng đúng cho bất đẳng thức không ngặt.
– Bất đẳng thức Cô-si
Định lí
Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng
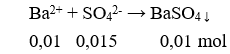
– Các hệ quả
Hệ quả 1
Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.
a + 1/a ≥ 2, ∀a > 0.
Hệ quả 2
Nếu x, y cùng dương và có tổng không đổi thì tích xy lớn nhất khi và chỉ khi x = y.
Hệ quả 3
Nếu x, y cùng dương và có tích không đổi thì tổng x + y nhỏ nhất khi và chỉ khi x = y.
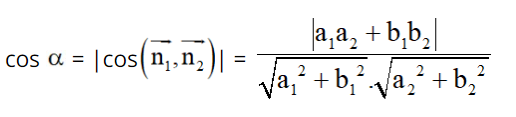
– Bất phương trình một ẩn
Bất phương trình ẩn x là mệnh đề chứa biến có dạng
f(x) < g(x) (f(x) ≤ g(x)) (1)
trong đó f(x) và g(x) là những biểu thức của x.
Ta gọi f(x) và g(x) lần lượt là vế trái của bất phương trình (1). Số thực x0 sao cho f(xo) < g(xo), (f(xo) ≤ g(xo)) là mệnh đề đúng được gọi là một nghiệm của bất phương trình (1).
Giải bất phương trình là tìm tập nghiệm của nó, khi tập nghiệm rỗng thì ta nói bất phương trình vô nghiệm.
Chú ý:
Bất phương trình (1) cũng có thể viết lại dưới dạng sau: g(x) > f(x) (g(x) ≥ f(x)).
– Điều kiện của một bất phương trình
Tương tự đối với phương trình, ta gọi các điều kiện của ẩn số x để f(x) và g(x) có nghĩa là điều kiện xác định (hay gọi tắt là điều kiện) của bất phương trình (1).
– Bất phương trình chứa tham số
Trong một bất phương trình, ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem như những hằng số và được gọi là tham số. Giải và biện luận bất phương trình chứa tham số là xét xem với các giá trị nào của tham số bất phương trình vô nghiệm, bất phương trình có nghiệm và tìm các nghiệm đó.
Hệ bất phương trình ẩn x gồm một số bất phương trình ẩn x mà ta phải tìm nghiệm chung của chúng.
Mỗi giá trị của x đồng thời là nghiệm của tất cả các bất phương trình của hệ được gọi là một nghiệm của hệ bất phương trình đã cho.
Giải hệ bất phương trình là tìm tập nghiệm của nó.
Để giải một hệ bất phương trình ta giải từng bất phương trình rồi lấy giao của các tập nghiệm.
– Bất phương trình tương đương
Ta đã biết hai bất phương trình có cùng tập nghiệm (có thể rỗng) là hai bất phương trình tương đương và dùng kí hiệu “<=>” để chỉ sự tương đương của hai bất phương trình đó.
Tương tự, khi hai hệ bất phương trình có cùng một tập nghiệm ta cũng nói chúng tương đương với nhau và dùng kí hiệu “<=>” để chỉ sự tương đương đó.
– Phép biến đổi tương đương
Để giải một bất phương trình (hệ bất phương trình) ta liên tiếp biến đổi nó thành những bất phương trình (hệ bất phương trình) tương đương cho đến khi được bất phương trình (hệ bất phương trình) đơn giản nhất mà ta có thể viết ngay tập nghiệm. Các phép biến đổi như vậy được gọi là các phép biến đổi tương đương.
– Cộng (trừ)
Cộng (trừ) hai vế của bất phương trình với cùng một biểu thức mà không làm thay đổi điều kiện của bất phương trình ta được một bất phương trình tương đương.
P(x) < Q(x) <=> P(x) – f(x) < Q(x) – f(x)
– Nhân (chia)
Nhân (chia) hai vế của bất phương trình với cùng một biểu thức luôn nhận giá trị dương (mà không làm thay đổi điều kiện của bất phương trình) ta được một bất phương trình tương đương. Nhân (chia) hai vế của bất phương trình với cùng một biểu thức luôn nhận giá trị âm (mà không làm thay đổi điều kiện của bất phương trình) và đổi chiều bất phương trình ta được một bất phương trình tương đương.
P(x) < Q(x) <=> P(x).f(x) < Q(x).f(x), f(x) > 0, ∀x
P(x) < Q(x) <=> P(x).f(x) > Q(x).f(x), f(x) < 0, ∀x
– Bình phương
Bình phương hai vế của một bất phương trình có hai vế không âm mà không làm thay đổi điều kiện của nó ta được một bất phương trình tương đương.
P(x) < Q(x) <=> P2(x) < Q2(x), P(x) ≥ 0, Q(x) ≥ 0, ∀x
– Chú ý
Trong quá trình biến đổi một bất phương trình thành bất phương trình tương đương cần chú ý những điều sau
Khi biến đổi các biểu thức ở hai vế của một bất phương trình thì điều kiện của bất phương trình có thể bị thay đổi. Vì vậy, để tìm nghiệm của một bất phương trình ta phải tìm các giá trị của x thỏa mãn điều kiện của bất phương trình đó và là nghiệm của bất phương trình mới.
Khi nhân (chia) hai vế của bất phương trình P(x) < Q(x) với biểu thức f(x) ta cần lưu ý đến điều kiện về dấu của f(x). Nếu f(x) nhận cả giá trị dương lẫn giá trị âm thì ta phải lần lượt xét từng trường hợp. Mỗi trường hợp dẫn đến hệ bất phương trình.
Khi giải bất phương trình P(x) < Q(x) mà phải bình phương hai vế thì ta lần lượt xét hai trường hợp
P(x), Q(x) cùng có giá trị không âm, ta bình phương hai vế bất phương trình.
P(x), Q(x) cùng có giá trị âm ta viết
P(x) < Q(x) <=> –Q(x) < –P(x)
rồi bình phương hai vế bất phương trình mới.
6. Kiến thức về Bảng phân bố tần số và tần suất:
Một số khái niệm cơ bản:
+) Một tập con hữu hạn các đơn vị điều tra được gọi là một mẫu.
+) Số phần tử của một mẫu được gọi là kích thước mẫu.
+) Các giá trị của dấu hiệu thu được trên mẫu được gọi là một mẫu số liệu.
Chú ý:Khi thực hiện điều tra thống kê (theo mục đích định trước), cần xác định tập hợp các đơn vị điều tra, dấu hiệu điều tra và thu thập các số liệu.
Định nghĩa:
Giả sử dãy n số liệu thống kê đã cho có k giá trị khác nhau (k ≤ n). Gọi xi là một giá trị bất kì trong k giá trị đó, ta có:
Tần số: số lần xuất hiện giá trị xi trong dãy số liệu đã cho gọi là tần số của giá trị đó, kí hiệu là ni.
Ví dụ: Trong bảng số liệu trên ta thấy có 7 giá trị khác nhau là
x1 = 4, x2 = 5, x3 = 6, x4 = 7, x5 = 8, x6 = 9, x7 = 10
x1 = 4 xuất hiện 3 lần => n1 = 3 (tần số của x1 là 3)
Tần suất: Số fi = ni/n được gọi là tần suất của giá trị xi (tỉ lệ của ni, tỉ lệ phần trăm)
Ví dụ: x1 có tần số là 3, do đó: f1 = 3/45 hay f1 = 5%
Bảng phân bố tần suất và tần số
| Tên dữ liệu | Tần số | Tần suất (%) |
| x1 x2 . . xk | n1 n2 . . nk | f1 f2 . . fk |
| Cộng | n1+…+nk | 100% |
Ví dụ:Bảng phân bố tần số và tần suất điểm kiểm tra 15’ môn toán 10CB
| Điểm toán | Tần số | Tần suất ( %) |
| 4 5 6 7 8 9 10 | 3 7 11 9 6 7 2 | 6,67 15,56 24,44 20 13,33 15,6 4,4 |
| Cộng | 45 | 100% |
Chú ý: Nếu bỏ cột tầng số thì ta được bảng phân bố tần suất; bỏ cột tần suất thì ta được bảng phân bố tần số.
4. Bảng phân bố tần số và tần suất ghép lớp
Giả sử p dãy số liệu thông kê đã cho được phân vào k lớp (k < n). Xét lớp thứ i trong k lớp đó, ta có:
Số ni các số liệu thông kê thuộc lớp thứ i được tần số của lớp đó.
Số fi = ni/n được gọi là tần số của lớp thứ i
Ví dụ: Theo bảng thông kê trên ta có thể phân thành 3 lớp [4;7], [7;9], [9;10]
| Lớp điểm toán | Tần số | Tần suất ( %) |
| [4;7] [7;9] [9;10] | 21 15 9 | 46,67 33,33 20 |
| Cộng | 45 | 100% |
Bảng này gọi là bảng phân bố tần số và tần suất ghép lớp. Nếu bỏ cột tần số thì ta được bảng phân bố tần suất ghép lớp; Nếu bỏ cột tần suất thì ta được bảng phân bố tần số ghép lớp.
7. Kiến thức về Cung và góc lượng giác:
Đường tròn định hướng và cung lượng giác
Đường tròn định hướng là một đường tròn trên đó ta chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ làm chiều dương.
Trên đường tròn định hướng cho hai điểm A và B. Một điểm M di động trên đường tròn luôn theo một chiều (âm hoặc dương) từ A đến B tạo nên một cung lượng giác có điểm đầu A điểm cuối B.
Với hai điểm A, B đã cho trên đường tròn định hướng ta có vô số cung lượng giác điểm đầu A, điểm cuối B. Mỗi cung như vậy đều được kí hiệu là
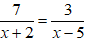
Góc lượng giác
Trên đường tròn định hướng cho một cung lượng giác Một điểm M chuyển động trên đường tròn từ C tới D tạo nên cung lượng giác nói trên. Khi đó tia OM quay xung quanh gốc O từ vị trí OC tới vị trí OD. Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC, tia cuối là OD.
Kí hiệu góc lượng giác đó là (OC, OD).
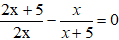
Đường tròn lượng giác
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn định hướng tâm O bán kính R = 1.
Đường tròn này cắt hai trục tọa độ tại bốn điểm
A(1; 0), A’(–1; 0); B(0; 1); B(0; –1).
Ta lấy A(1; 0) làm điểm gốc của đường tròn đó.
Đường tròn xác định như trên được gọi là đường tròn lượng giác (gốc A).
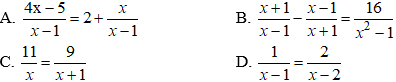
Độ và radian
a) Đơn vị radian
Trên đường tròn tùy ý, cung có độ dài bằng bán kính được gọi là cung có số đo 1 rad.
b) Quan hệ giữa độ và radian

c) Độ dài của một cung tròn
Trên đường tròn bán kính R, cung nửa đường tròn có số đo là π rad và có độ dài là πR. Vậy cung có số đo α rad của đường tròn bán kính R có độ dài
l = Rα.
Số đo của một cung lượng giác
Số đo của một cung lượng giác ![]() (A ≠ M) là một số thực âm hay dương.
(A ≠ M) là một số thực âm hay dương.
Kí hiệu số đo của cung ![]() là sđ
là sđ ![]() .
.
Ghi nhớ
Số đo của các cung lượng giác có cùng điểm đầu và điểm cuối sai khác nhau một bội của 2π.
Ta viết
sđ ![]() = α + k2π , k ∈ Z
= α + k2π , k ∈ Z
trong đó α là số đo của một cung lượng giác tùy ý có điểm đầu là A, điểm cuối là M
Số đo của một góc lượng giác
Số đo của góc lượng giác (OA, OC) là số đo của cung lượng giác AC tương ứng.
Chú ý Vì mỗi cung lượng giác ứng với một góc lượng giác và ngược lại, đồng thời số đo của các cung và góc lượng giác tương ứng là trùng nhau, nên từ nay về sau khi ta nói về cung thì điều đó cũng đúng cho góc và ngược lại.
Chọn điểm gốc A(1; 0) làm điểm đầu của tất cả các cung lượng giác trên đường tròn lượng giác. Để biểu diễn cung lượng giác có số đo α trên đường tròn lượng giác ta cần chọn điểm cuối M của cung này. Điểm cuối M được xác định bởi hệ thức sđ ![]() = α
= α
Giá trị lượng giác của các cung đặc biệt
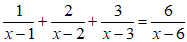
Công thức lượng giác cơ bản
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau
sin2α + cos2α = 1
Giá trị lượng giác của các cung có liên quan đặc biệt
1) Cung đối nhau: α và –α
cos(-α) = cosα
sin(-α) = –sinα
tan(-α) = –tanα
cot(-α) = –cotα
2) Cung bù nhau: α và π-α
sin(π-α) = sinα
cos(π-α) = –cosα
tan(π-α) = –tanα
cot(π-α) = –cotα
3) Cung hơn kém π : α và (α + π)
sin(α + π) = –sinα
cos(α + π) = –cosα
tan(α + π) = tanα
cot(α + π) = cotα
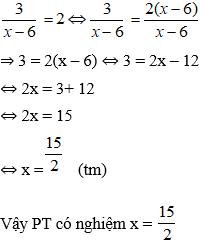
8. Kiến thức về Véc tơ:
Khái niệm vectơ
Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểu đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.
Định nghĩa. Vectơ là một đoạn thẳng có hướng.
Vectơ có điểm đầu A, điểm cuối B được kí hiệu là ![]() và đọc là “ vectơ AB “. Để vẽ được vectơ
và đọc là “ vectơ AB “. Để vẽ được vectơ ![]() ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.
ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.

Vectơ còn được kí hiệu là ![]() khi không cần chỉ rõ điểm đầu và điểm cuối của nó.
khi không cần chỉ rõ điểm đầu và điểm cuối của nó.
Vectơ cùng phương, vectơ cùng hướng
Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
Định nghĩa. Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Nhận xét. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ ![]() cùng phương.
cùng phương.
Hai vectơ bằng nhau
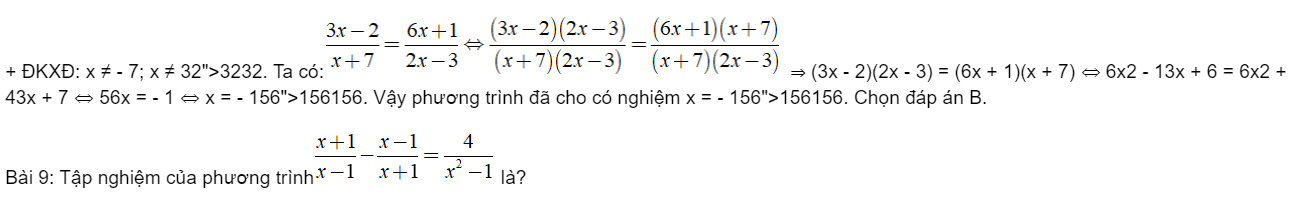
Vectơ – không
Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.
Bây giờ với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu và được gọi là vectơ – không.
Tổng của hai vectơ
 Quy tắc hình bình hành
Quy tắc hình bình hành
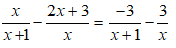
Hiệu của hai vectơ
a) Vectơ đối
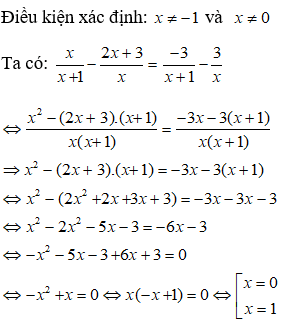
b) Định nghĩa hiệu của hai vectơ
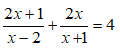
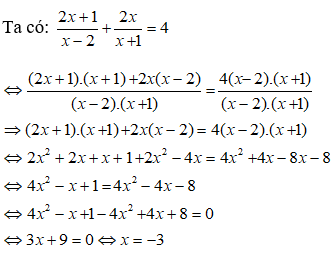
9. Kiến thức về Tích vô hướng của hai vectơ và ứng dụng:
Định nghĩa
Với mỗi góc α (0o ≤ α ≤ 180o) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho ∠ xOM = α và giả sử điểm M có tọa độ M(xo, yo).
Khi đó ta có định nghĩa:
sin của góc α là yo, kí hiệu sinα = yo;
cosin của góc α là xo, kí hiệu cosα = xo
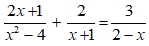
Tính chất
Trên hình bên ta có dây cung NM song song với trục Ox và nếu ∠ xOM = α thì ∠xON = 180o – α. Ta có yM = yN = yo, xM = –xN = xo. Do đó
sin α = sin(180o – α)
cos α = –cos(180o – α)
tan α = –tan(180o – α)
cot α = –cot(180o – α)
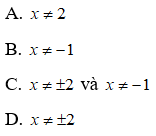
Giá trị lượng giác của các góc đặc biệt

Trong bảng kí hiệu “||” để chỉ giá trị lượng giác không xác định.
Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.
Góc giữa hai vectơ
 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ
Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:
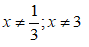
Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
Biểu thức tọa độ của tích vô hướng
Ứng dụng
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A(xA; yA) và B(xB; yB) được tính theo công thức:
![]()
10. Kiến thức về Phương pháp tọa độ trong mặt phẳng: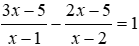
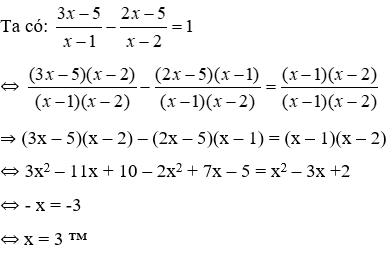
Nhận xét.
+) Một đường thẳng có vô số vectơ pháp tuyến.
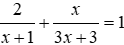
Phương trình tổng quát của đường thẳng
Đường thẳng ∆ đi qua điểm M0(x0, y0) và có VTPT vecto n = (A; B)
=> phương trình tổng quát của đường thẳng ∆ có dạng
A(x – x0) + B(y – y0) = 0 hay Ax + By + C = 0 với C = –Ax0 – By0.
Nhận xét.
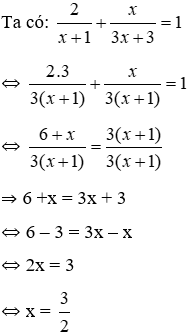
Phương trình này được gọi là phương trình đường thẳng theo đoạn chắn, đường thẳng này cắt Ox và Oy lần lượt tại M(a0; 0) và N(0; b0).
Vị trí tương đối của hai đường thẳng Xét hai đường thẳng có phương trình tổng quát là
∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0
Tọa độ giao điểm của ∆1 và ∆2 là nghiệm của hệ phương trình:
Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án
+) Nếu hệ có một nghiệm (x0; y0) thì ∆1 cắt ∆2 tại điểm M0(x0, y0).
+) Nếu hệ có vô số nghiệm thì ∆1 trùng với ∆2.
+) Nếu hệ vô nghiệm thì ∆1 và ∆2 không có điểm chung, hay ∆1 song song với ∆2
Cách 2. Xét tỉ số
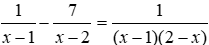
Góc giữa hai đường thẳng
Cho hai đường thẳng
∆1: a1x + b1y + c1 = 0 có VTPT Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án = (a1; b1);
∆2: a2x + b2y + c2 = 0 có VTPT Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án = (a2; b2);
Gọi α là góc tạo bởi giữa hai đường thẳng ∆1 và ∆2
Khi đó
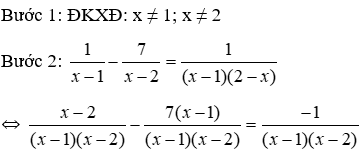
11. Các dạng bài tập Toán 10 chi tiết:
Các dạng bài tập Đại số lớp 10
Chuyên đề: Mệnh đề – Tập hợp
Xác định tính đúng sai của mệnh đề
Mệnh đề và suy luận toá học
Các bài toán liên quan đến mệnh đề phủ định
Tập hợp và cách xác định tập hợp
Các phép toán trên tập hợp
Các bài toán về các tập hợp số
Các bài toán liên quan đến số gần đúng và sai số
Chuyên đề: Mệnh đề
Dạng 1: Xác định tính đúng sai của mệnh đề
Dạng 2: Phát biểu mệnh đề điều kiện cần và đủ
Dạng 3: Phủ định mệnh đề
Bài tập tổng hợp về mệnh đề (có đáp án)
Chuyên đề: Tập hợp và các phép toán trên tập hợp
Lý thuyết Tập hợp và các phép toán trên tập hợp
Dạng 1: Cách xác định tập hợp
Dạng 2: Các phép toán trên tập hợp
Dạng 3: Giải toán bằng biểu đồ Ven
Bài tập Tập hợp và các phép toán trên tập hợp (có đáp án)
Chuyên đề: Số gần đúng và sai số
Lý thuyết Số gần đúng và sai số
Bài tập Số gần đúng và sai số (có đáp án)
Bài tập tổng hợp Chương Mệnh đề, Tập hợp (có đáp án)
Bài tập chương Mệnh đề, Tập hợp (Tự luận)
Bài tập chương Mệnh đề, Tập hợp (Trắc nghiệm – phần 1)
Bài tập chương Mệnh đề, Tập hợp (Trắc nghiệm – phần 2)
Chuyên đề: Hàm số bậc nhất và bậc hai
Chủ đề: Đại cương về hàm số
Các dạng bài tập về hàm số và cách giải
Các dạng bài tập về hàm số bậc nhất và cách giải
Các dạng bài tập về hàm số bậc hai và cách giải
Dạng 1: Tìm tập xác định của hàm số
Dạng 2: Xét tính chẵn lẻ của hàm số
Dạng 3: Xét tính đơn điệu (đồng biến, nghịch biến) của hàm số
Dạng 4: Bài tập về đồ thị hàm số
Bài tập tổng hợp: Bài tập về hàm số
Chủ đề: Hàm số bậc nhất
Dạng 1: Xác định hàm số y = ax + b và sự tương giao của đồ thị hàm số
Dạng 2: Xét sự biến thiên và vẽ đồ thị hàm số bậc nhất
Dạng 3: Đồ thị hàm số chứa dấu giá trị tuyệt đối
Dạng 4: Ứng dụng của hàm số bậc nhất trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất
Bài tập tổng hợp: Bài tập về hàm số bậc nhất
Chủ đề: Hàm số bậc hai
Dạng 1: Xác định Hàm số bậc hai
Dạng 2: Xét sự biến thiên và vẽ đồ thị hàm số bậc hai
Dạng 3: Đồ thị hàm số chứa dấu giá trị tuyệt đối và cho bởi nhiều công thức
Dạng 4: Ứng dụng của hàm số bậc hai trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất
Bài tập tổng hợp: Bài tập về hàm số bậc hai