Để giúp các bạn học sinh củng cố kiến thức về phương trình bậc nhất, phương trình bậc hai, định lý Vi – ét trong chương trình Đại số đã được học ở cấp hai, bài viết dưới đây sẽ giới thiệu đến các bạn các kiến thức liên quan đến phương trình quy về phương trình bậc nhất, bậc hai và một số dạng bài tập liên quan.
Mục lục bài viết
1. Phương trình bậc nhất:
Phương trình có dạng ax + b = 0 (1), với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.
– Nếu a = 0 và b = 0 thì phương trình (1) có vô số nghiệm
– Nếu a = 0 và b ≠ 0 thì phương trình (1) vô nghiệm
– Nếu a ≠ 0 và b ≠ 0 thì phương trình (1) có nghiệm duy nhất x = – b/a.
2. Phương trình bậc hai:
Phương trình bậc hai là phương trình có dạng: ax2 + bx + c = 0 (a≠0) (1)
Trong đó: x là ẩn số
a, b, c: là các số đã biết gắn với biến x sao cho: a ≠ 0.
Giải phương trình bậc 2 là đi tìm các giá trị của x sao cho khi thay x vào phương trình (1) thì thỏa mãn ax2+ bx+c=0.
Bước 1: Tính Δ=b2-4ac
Bước 2: So sánh Δ với 0
– Nếu Δ>0: phương trình tồn tại 2 nghiệm: x1 = (-b + √Δ )/2a và x2 = (-b – √Δ )/2a
– Nếu Δ=0, phương trình có nghiệm kép x= – b/2a
– Nếu Δ<0, phương trình đã cho vô nghiệm.
Trong trường hợp b = 2b’, để đơn giản ta có thể tính Δ’ = b’2 – ac, tương tự như trên:
– Nếu Δ’ < 0 thì phương trình bậc 2 vô nghiệm.
– Nếu Δ’ = 0 thì phương trình bậc 2 có nghiệm kép x1 = x2 = -b’/a.
– Nếu Δ’ > 0 thì phương trình bậc 2 có nghiệm x1 = (-b’ + √Δ’ )/a và x2 = (-b’ – √Δ’ )/a
3. Định lí Vi–ét:
Công thức Vi-ét về quan hệ giữa các nghiệm của đa thức với các hệ số của nó. Trong trường hợp phương trình bậc hai một ẩn, được phát biểu như sau:
Gọi x1, x2 là nghiệm của phương trình bậc 2 một ẩn ax2 + bx + c (a≠0) thì:
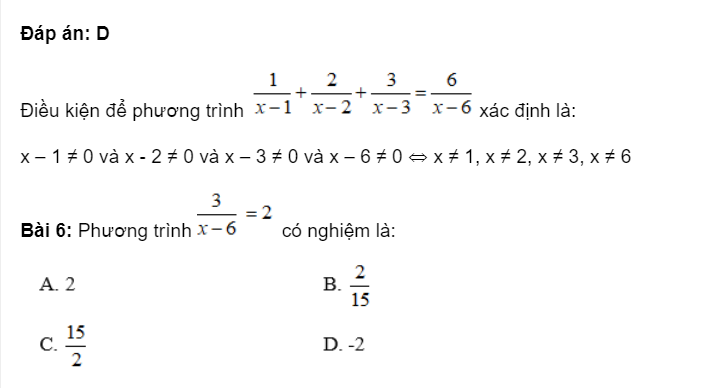
– Nếu S<0, x1 và x2 trái dấu.
– Nếu S>0, x1 và x2 cùng dấu:
– P>0, hai nghiệm cùng dương.
– P<0, hai nghiệm cùng âm.
Định lý Vi-ét đảo:
Nếu x1 + x2 = S và x1 . x2 = P thì x1, x2 là 2 nghiệm của phương trình x2 – Sx + P=0 (Điều kiện S2 – 4P>0)
4. Các phương trình quy về phương trình bậc nhất, bậc hai:
4.1. Dạng 1: Phương trình chứa ẩn trong dấu giá trị tuyệt đối:
Cách giải phương trình chứa ẩn trong dấu giá trị tuyệt đối là đặt các điều kiện xác định để đưa phương trình có dấu giá trị tuyệt đối thành phương trình không dấu giá trị tuyệt đối. Ta tìm cách để khử dấu giá trị tuyệt đối, bằng cách:
– Dùng định nghĩa hoặc tính chất của GTTĐ.
– Bình phương hai vế.
– Đặt ẩn phụ.
Phương trình dạng |f(x)|=|g(x)| ta có thể giải bằng cách biến đổi tương đương như sau:
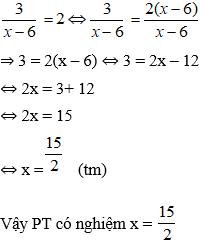
hoặc |f(x)| = |g(x)|⇔ f2(x) = g2(x)
– Đối với phương trình dạng |f(x)| = g(x)(*) ta có thể biến đổi tương đương như sau:
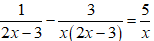
Hoặc
Ví dụ minh họa
Ví dụ 1: Giải phương trình |3x – 2| = x2 + 2x + 3
Lời giải:
Ta có: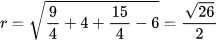
* Nếu x ≥ 2/3 ⇒ PT ⇔ 3x – 2 = x2 + 2x + 3 ⇔ x2 – x + 5 = 0 pt vô nghiệm
* Nếu x < 2/3 ⇒ PT ⇔ -3x + 2 = x2 + 2x + 3 ⇔ x2 + 5x + 1 = 0
⇔ x = (-5 ± √21)/2 hai nghiệm này đều thỏa mãn x < 2/3
Vậy nghiệm của phương trình đã cho là x = (-5 ± √21)/2
Ví dụ 2: Giải phương trình |x3 – 1| = |x2 – 3x + 2|
Lời giải:
Hai về không âm bình phương hai vế ta có
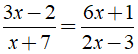
Vậy tập nghiệm của phương trình đã cho là S = {1; -1 + √2; -1 – √2}
Ví dụ 3: Phương trình (x+1)2 – 3|x+1| + 2 = 0 có bao nhiêu nghiệm?
Lời giải:
Đặt t = |x + 1|, t ≥ 0
Phương trình trở thành t2 – 3t + 2 = 0 ⇔ 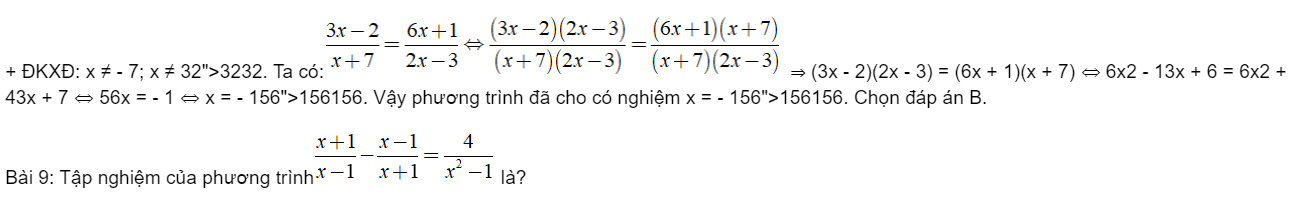
Với t = 1 ta có |x + 1| = 1 ⇔ x + 1 = ±1 ⇔ 
Với t = 2 ta có |x + 1| = 2 ⇔ x + 1 = ±2 ⇔ ![]()
Vậ
4.2. Dạng 2: Phương trình chứa ẩn ở mẫu:
Phương trình chứa ẩn ở mẫu là phương trình có biểu thức chứa ẩn ở dưới mẫu.
Để giải phương trình chứa ẩn ở mẫu, ta sẽ giải theo các bước như sau:
– Bước 1: Tìm ĐKXĐ (Điều kiện xác định) của ẩn tại phương trình.
Ví dụ: Tìm điều kiện xác định của các phương trình sau (x – 1)/(x + 2) + 1 = 1/(x – 2).
Hướng dẫn: Ta thấy x + 2 ≠ 0 khi x ≠ – 2 và x – 2 ≠ 0 khi x ≠ 2.
Do đó ĐKXĐ của phương trình (x – 1)/(x + 2) + 1 = 1/(x – 2) là x ≠ ± 2.
– Bước 2: Khử mẫu bằng cách quy đồng mẫu thức hai vế.
– Bước 3: Giải phương trình vừa sau bước 2.
– Bước 4: So sánh các nghiệm vừa tìm được tại bước 3 với ĐKXĐ và đưa ra kết luận.
Vì chứa ẩn ở dưới mẫu (đại lượng chưa biết) nên chưa thể khẳng định mẫu thức khác 0. Đây là điều kiện bắt buộc để một phân thức tồn tại (hay có nghĩa). Vì vậy việc tìm điều kiện xác định rất quan trọng trong việc tìm nghiệm của một phương trình để từ đó giúp loại bỏ các giá trị của ẩn làm cho mẫu thức bằng 0.
Ví dụ minh họa
Ví dụ 1: Giải phương trình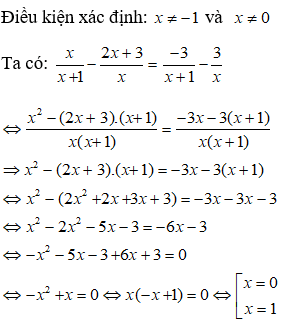
Lời giải:
Bước 1: Điều kiện xác định: x ≠ 0; x ≠ 2.
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu
Ta có: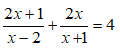
⇒ 2(x – 2)(x + 2) = x(2x + 3)
Bước 3: Giải phương trình
Ta có: 2(x – 2)(x + 2) = x(2x + 3) ⇔ 2(x2 – 4) = 2x2 + 3x
⇔ 2x2 – 8 = 2x2 + 3x ⇔ 3x = – 8 ⇔ x = – 8/3.
Bước 4: Kết luận
So sánh với ĐKXĐ, ta thấy x = – 8/3 thỏa mãn.
Vậy phương trình đã cho có tập nghiệm S = { – 8/3 }.
Ví dụ 2: Giải phương trình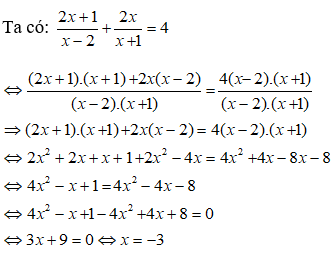
Lời giải:
+ ĐKXĐ: x ≠ 0; x ≠ – 5.
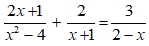
⇒ (2x + 5)(x + 5) – 2x2 = 0
⇔ 2x2 + 10x + 5x + 25 – 2x2 = 0 ⇔ 15x = – 25 ⇔ x = – 5/3.
+ So sánh với ĐKXĐ ta thấy x = – 5/3 thỏa mãn điều kiện.
Vậy phương trình đã cho có tập nghiệm là S = {- 5/3}.
4.3. Dạng 3: Phương trình chứa ẩn trong căn:
Để giải phương trình chứa ẩn dưới dấu căn ta tìm cách để khử dấu căn, bằng cách:
– Nâng luỹ thừa hai vế.
– Phân tích thành tích.
– Đặt ẩn phụ.
Các dạng phương trình sau ta có thể giải bằng cách thực hiện phép biến đổi tương đương:
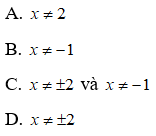
Phương trình có dạng a.f(x) + b.√(f(x) ) + c = 0 ta đặt √(f(x)) = t
Ngoài ra ta còn có phương pháp phân tích thành tích bằng cách nhân liên hợp

Với A, B không đồng thời bằng không
Ví dụ minh họa
Ví dụ 1: Giải phương trình sau √(2x-3) = x-3
Lời giải:
Ta có
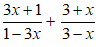
Ví dụ 2: Giải phương trình sau![]()
Lời giải:
Phương trình tương đương với phương trình
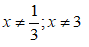
Vậy phương trình có nghiệm là x = 0 và x = 1
Ví dụ 3: Giải phương trình sau √(2x-1) + x2 – 3x + 1 = 0
Lời giải:
Ta có
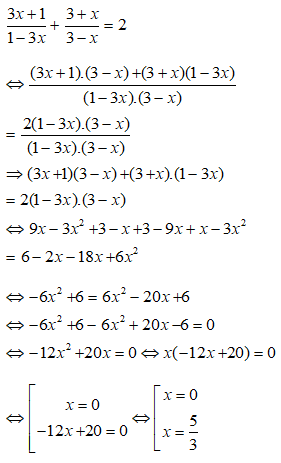
Vậy phương trình có nghiệm là x = 1 và x = 2 – √2
Ví dụ 4: Giải phương trình sau x2 + √(x2 + 11) = 31
Lời giải:
Đặt t = √(x2 + 11), t ≥ 0. Khi đó phương trình đã cho trở thành:
t2 + t – 42 = 0 ⇔ ![]()
Vì t ≥ 0 ⇒ t = 6, thay vào ta có √(x2 + 11) = 6
x2 + 11 = 36 ⇔ x = ±5
Vậy phương trình có nghiệm là x = ±5
Ví dụ 5: Giải phương trình sau![]()
Lời giải:
Đặt t = √(3x2 – 2x + 2), điều kiện t ≥ 0. Khi đó √(3x2 – 2x + 9) = √(t2 + 7)
Phương trình trở thành √(t2 + 7) + t = 7
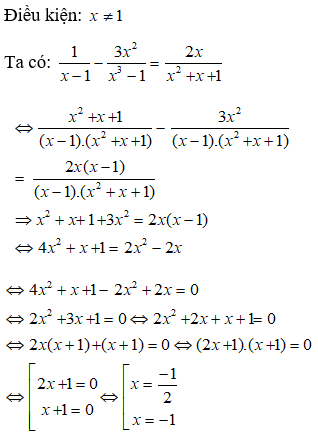
Vậy phương trình có hai nghiệm x = (1 ± √22)/3
4.4. Dạng 4: Phương trình trùng phương:
Phương trình trùng phương là kiểu phương trình có dạng: ax4 + bx2 + c = 0 (a≠0) (1)
Cách giải phương trình trùng phương:
– Bước 1: Đưa phương trình về phương trình bậc hai bằng cách đặt ẩn phụ t = x2 (t≥0) để: at2 + bt + c = 0 (a≠0) (2)
– Bước 2: Giải phương trình bậc hai ẩn t.
– Bước 3: Giải phương trình x2 = t để tìm nghiệm .
– Bước 4: Kết luận.
Biện luận số nghiệm của phương trình trùng phương
+) Phương trình (1) có 4 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm dương phân biệt.
+) Phương trình (1) có 3 nghiệm phân biệt ⇒ phương trình (2) có 1 nghiệm dương và một nghiệm t = 0.
+) Phương trình (1) có 2 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm trái dấu hoặc có nghiệm kép dương.
+) Phương trình (1) có duy nhất 1 nghiệm ⇒ phương trình (2) có nghiệm kép x = 0 hoặc có một nghiệm x = 0 và một nghiệm âm.
+) Phương trình (1) vô nghiệm ⇒ phương trình (2) vô nghiệm hoặc có hai nghiệm âm.
Ví dụ minh họa: Giải phương trình x4−5x2+4=0
Lời giải:
Đặt t=x2. Điều kiện t≥0
Khi đó phương trình đã cho trở thành :
t2−5t+4=0
⇔(t−1)(t−4)=0⇔t=1 hoặc t=4
Vậy nên:
x2=1 hoặc x2=4 ⇔ x=±1 hoặc x=±2
Vậy phương trình đã cho có 4 nghiệm phân biệt : x=−1;1;−2;2
Một số phương trình trùng phương biến đổi x→1/x hoặc các biểu thức chứa căn thì đầu tiên ta cần tìm điều kiện của phương trình trùng phương rồi mới tiến hành giải




